Recombination is a general process in which multi-component entities physically interact and mutually exchange components to create chimeric products or offspring. While the concept is most often applied to the heredity actions that occur in the living world, parallels exist in chemistry, physics, engineering, and many other scientific disciplines. A simple instance of recombination can be symbolized as: \[ A\bullet B + C\bullet D \longrightarrow A\bullet D + C\bullet B \] where $$A$$, $$B$$, $$C$$ and $$D$$ represent potentially swappable components, the symbol $$\bullet$$ represents a concrete connection or bond between the components, and $$A\bullet B, C\bullet D, \ldots$$ represent complete entities with some sort of ascribable value in the system. In the realm of chemical physics for example, one can describe the process of nucleosynthesis as the recombination of existing nuclei to generate new ones. In the realm of biology, recombination of existing genes or genomes can create theretofore novel genotypes. In any event, a characteristic feature of recombination is that relatively large blocks of an underlying material are exchanged among individuals, rather than an alternative process in which new whole entities are made by piecing together minimal subunits, one-at-a-time. If each block contains quantifiable information, then the complexity of the system as a whole can be significantly affected by recombination events.
Assignment
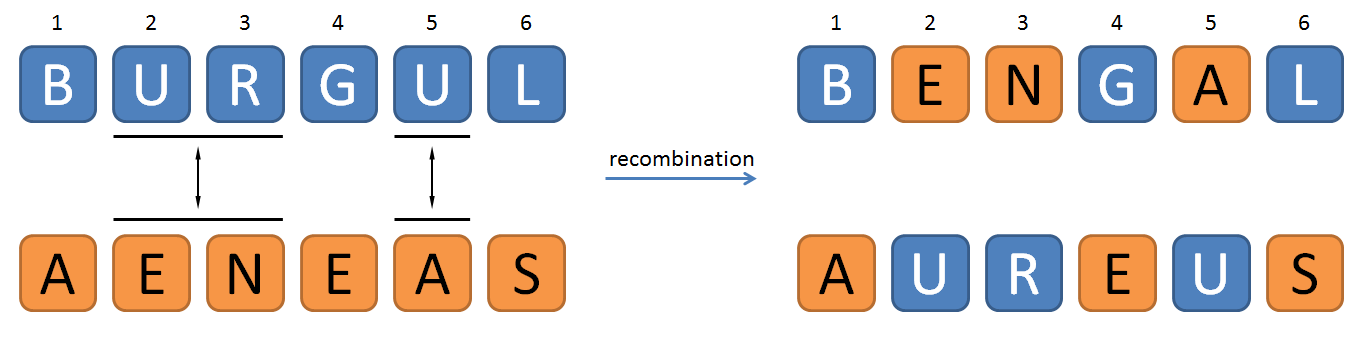
Recombination may also be applied to natural language. If we start with two words that have equal length, recombination can be defined as the process in which corresponding sequences of one or more successive letters are exchanged between these two words. Accidentally, such a recombination might result in two existing words. Say, for example, that we start from the following two words:
BURGUL: cereal food made from the groats of several different wheat species, most often from durum wheat
AENEAS: Trojan hero in Greco-Roman mythology, son of the prince Anchises and the goddess Venus (Aphrodite)
If we then number the positions of the letters in the words from left to right, starting at 1, and exchange the letters at positions 2, 3 and 5, we get two other existing words:
BENGAL: geographical and ethno-linguistic region in South Asia
AUREUS: gold coin of ancient Rome valued at 25 silver denarii
This recombination of the words BURGUL and AENEAS may be represented as
In this exercise we only consider words that contain letters. Your task is to write two functions that each take two or three words. All words passed to one of these functions should have equal length. If this is not the case, the functions must raise an AssertionError with the message words must have equal length. Raising this AssertionError always takes precedence over any other exceptions that are explicitly raised by the functions.
Write a function recombination that takes three words. If the third word can result from a recombination between the first two words, the function must return the other word that results from this recombination. In case the third word can not result from a recombination between the first two words, the function must raise an AssertionError with the message invalid recombination.
Write a function chimeras that takes three arguments. The first two arguments are words. The function must return a tuple containing the two words that result after recombination of the two given words. The third argument is a string that describes the fragments that must be exchanged during this recombination. Each fragment is a sequence of one or more consecutive letters that is described as m-n, with m being the start position of the sequence and n its final position. Positions of the letters in a word are numbered from left to right, starting at 1. The fragments are separated from each other by semicolons (;). A fragment that only contains a single letter is not represented as n-n, but simply as n.
Example
>>> recombination('burgul', 'aeneas', 'bengal')
'aureus'
>>> recombination('oleins', 'arcade', 'oreads')
'alcine'
>>> recombination('alevin', 'elodea', 'alodia')
'eleven'
>>> recombination('nitrogen', 'fluorine', 'tin')
Traceback (most recent call last):
AssertionError: words must have equal length
>>> recombination('nitrogen', 'fluorine', 'aluminium')
Traceback (most recent call last):
AssertionError: words must have equal length
>>> recombination('nitrogen', 'fluorine', 'ringtone')
Traceback (most recent call last):
AssertionError: invalid recombination
>>> chimeras('burgul', 'aeneas', '2-3;5')
('bengal', 'aureus')
>>> chimeras('oleins', 'arcade', '2;4-5')
('oreads', 'alcine')
>>> chimeras('alevin', 'elodea', '2-4;6')
('alodia', 'eleven')
>>> chimeras('nitrogen', 'aluminium', '3-7')
Traceback (most recent call last):
AssertionError: words must have equal length