Lineaire regressie
Om accurate en interpreteerbare resultaten te bekomen gaat men vaak bepaalde veronderstellingen doen over de structuur van \(g(x)\). Zo modelleert men \(g(x)\) vaak als een lineaire functie van ongekende parameters. Dat wordt geïllustreerd in Figuur 28.
- pipe dataset naar ggplot
- selecteer data
ggplot(aes(x=ESR1,y=S100A8)) - voeg punten toe met
geom_point() - voeg een “smooth line” toe
geom_smooth() - voeg een rechte toe
geom_smooth()metmethod = "lm"(linear model). (We zettense = FALSEom geen puntgewijze betrouwbaarheidsintervallen weer te geven)
brcaSubset %>%
ggplot(aes(x = ESR1, y = S100A8)) +
geom_point() +
geom_smooth(se = FALSE, col = "grey") +
geom_smooth(method = "lm", se = FALSE)
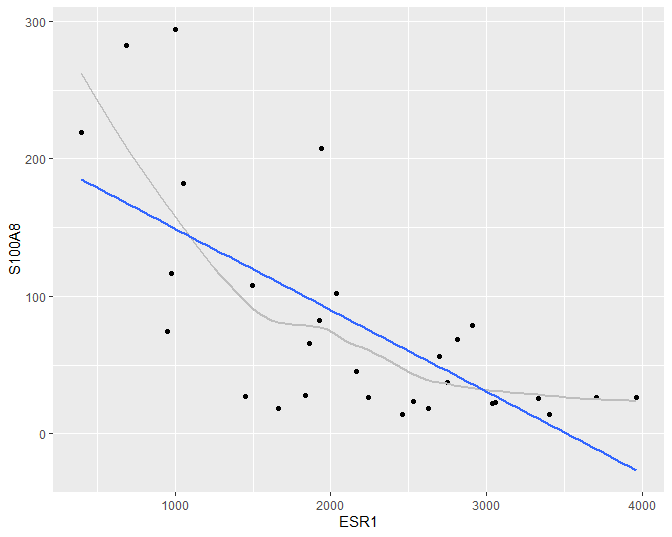
Figuur 28: Scatterplot voor S100A8 expressie in functie van de ESR1 expressie met lineair model dat het verband tussen beide genen samenvat (na verwijdering van outliers in de S100A8 expressie, merk op dat we deze outliers in principe niet mochten verwijderen uit de dataset zoals we verder in dit hoofdstuk zullen zien).
Men veronderstelt dan het onderstaande lineaire regressiemodel
\[\begin{equation} E(Y|X =x)=\beta_0 + \beta_1 x \qquad(2) \end{equation}\]waarbij \(\beta_0\) en \(\beta_1\) ongekende modelparameters zijn. In deze uitdrukking stelt \(E(Y|X=x)\) de waarde op de \(Y\)-as voor, \(x\) de waarde op de \(X\)-as, het intercept \(\beta_0\) stelt het snijpunt met de \(Y\)-as voor en de helling \(\beta_1\) geeft de richtingscoëfficiënt van de rechte weer. Uitdrukking (2) wordt een statistisch model genoemd. Merk op dat dit model enkel een onderstelling maakt over het gemiddelde van de S100A8 expressie.
Deze naamgeving suggereert dat het bepaalde onderstellingen legt op de verdeling van de geobserveerde gegevens. In het bijzonder onderstelt het dat de gemiddelde uitkomst lineair varieert in functie van één verklarende variabele \(X\). Om die reden wordt Model (2) ook een enkelvoudig lineair regressiemodel genoemd. Onder dit model kan elke meting \(Y\) op een foutterm \(\epsilon\) na beschreven worden als een lineaire functie van de verklarende variabele \(X\), verder in deze cursus ook de predictor genoemd:
\[Y=E(Y|X=x)+\epsilon=\beta_0+\beta_1 x+\epsilon\]waarbij \(\epsilon\) de afwijking tussen de uitkomst en haar (conditioneel) gemiddelde waarde voorstelt, dit is de onzekerheid in de responsvariabele.
Gezien het lineair regressiemodel onderstellingen doet over de verdeling van X en Y , kunnen deze onderstellingen ook vals zijn. Later in dit hoofdstuk zullen we zien hoe deze onderstellingen geëvalueerd kunnen worden. Als echter voldaan is aan de onderstellingen, laat dit een efficiënte data-analyse toe: alle observaties worden benut om te leren over verwachte uitkomst bij X = x.
Het lineair regressiemodel kan worden gebruikt voor
- predictie (voorspellingen): als \(Y\) ongekend is, maar \(X\) wel
gekend is, kunnen we \(Y\) voorspellen op basis van \(X\)
- associatie: beschrijven van de biologische relatie tussen variabele \(X\) en continue meting \(Y\):
waarbij \(\beta_1\) het verschil is in gemiddelde uitkomst tussen subjecten die 1 eenheid verschillen in de genexpressie van het ESR1 gen.