A transposition cipher is a method of encryption in which the characters of a plaintext are shuffled according to a regular system, so that the ciphertext constitutes a permutation of the plaintext. This process must be reversible so that the plaintext can be reconstructed from the ciphertext.

One of the techniques regularly used in traditional cryptography is called columnar transposition. This technique uses a keyword that only contains letters to determine how the characters of the plaintext must be shuffled. The easiest way to explain how columnar transposition works is by means of an example. Suppose we want to encrypt the message

It Ain't What You Do...

with the keyword BANANARAMA.

We first reduce the keyword by only retaining the first occurrence of each letter, without making a distinction between uppercase and lowercase letters. This way, the keyword BANANARAMA is reduced to BANRM, in which all letters are unique.

We then fill a rectangular grid from left to right and from top to bottom with the consecutive characters of the message. The number of columns of the grid corresponds to the number of unique letters in the keyword (= number of letters in the reduced keyword). If the last row of the grid is not completely filled, it is completed with question marks (?). The keyword BANANARAMA has 5 unique letters, so the letters of the message

It Ain't What You Do...

are written out as follows in a grid with 5 columns. The last row is completed with two question marks (marked in yellow).

Encryption of the sentence It Ain't What You Do... using columnar transposition with the keyword BANANARAMA.

Next, we number the columns of the grid based on the alphabetic order of the letters in the reduced keyword. We start numbering from zero. For the reduced keyword BANRM, the columns are numbered consecutively with 1, 0, 3, 4 and 2. Below we show how the columns are numbered for some additional keywords:

keyword	reduced	column numbering	column order
`BANANARAMA`	`BANRM`	1, 0, 3, 4, 2	1, 0, 4, 2, 3
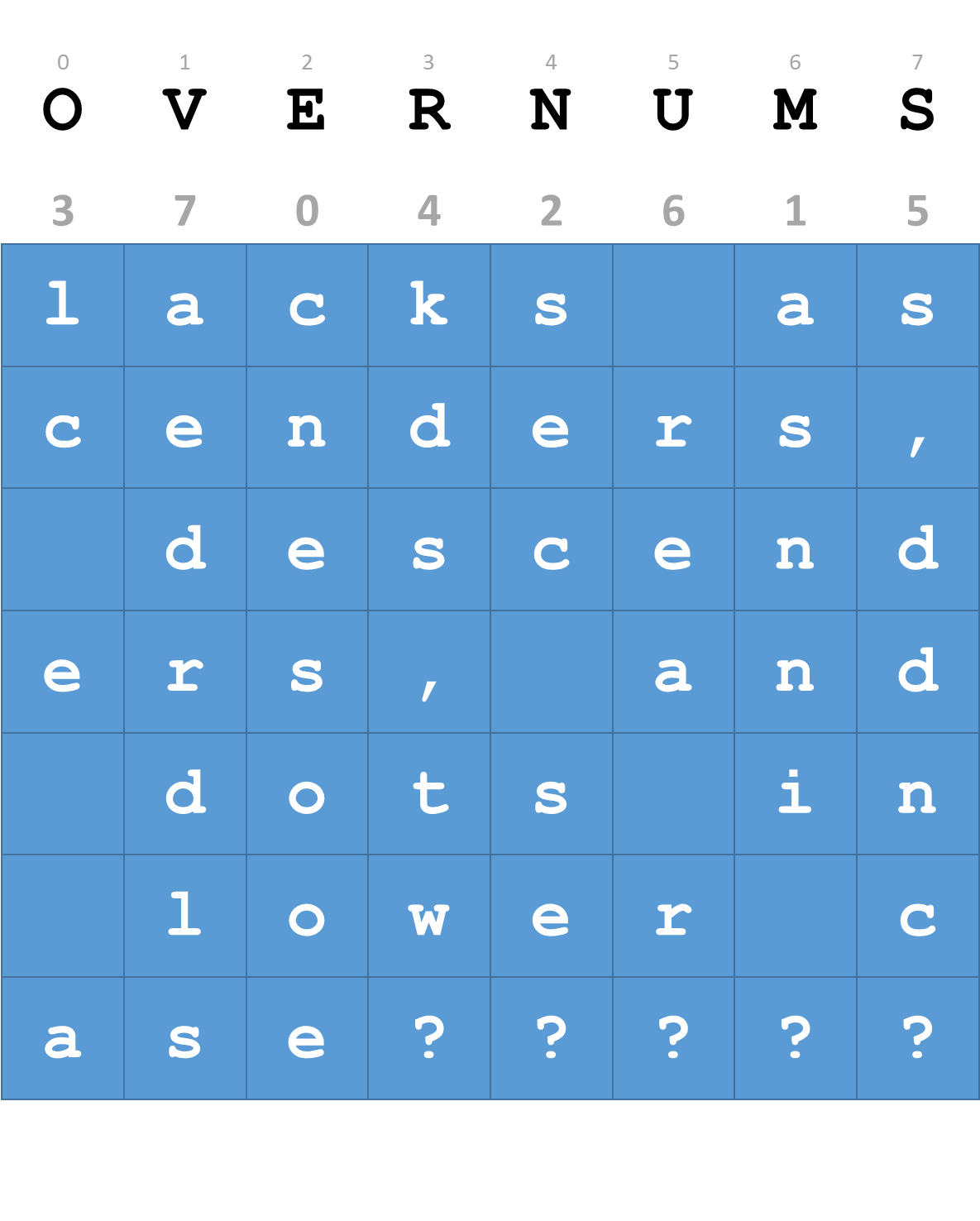
`overnumerousnesses`	`OVERNUMS`	3, 7, 0, 4, 2, 6, 1, 5	2, 6, 4, 0, 3, 7, 5, 1
`Mississippi`	`MISP`	1, 0, 3, 2	1, 0, 3, 2

Finally, we obtain the ciphertext by reading out the characters from the grid column by column, where each column is read top to bottom and the columns are traversed in increasing order based on their column numbering. For the example grid we first get the letters t'au. from the second column (uppercase letter A), then the letters Inho. from the first column (uppercase letter B), then the letters iWYO? from the last column (uppercase letter M), and so on. This way, the message is encrypted as

t'au.Inho.iWYo? tt .A D?

Does this make any sense?

Assignment

A keyword is a string that only contains letters (uppercase and lowercase letters). Your task:

Write a function reduce that takes a keyword. The function must return the reduced keyword, with all letters converted to uppercase.
Write a function column_indexing that takes a keyword. The function must return a tuple that indicates how the columns of the grid are numbered in a columnar transposition with the given keyword.
Write a function column_order that takes a keyword. The function must return a tuple that indicates in which order the columns are traversed in a columnar transposition with the given keyword.
Write a function encode that takes a plaintext (str) and a keyword. The function must return the ciphertext (str) that results from encrypting the given plaintext using columnar transposition with the given keyword.
Write a function decode that takes two arguments: i) a ciphertext (str) that results from columnar transposition and ii) the keyword used in the columnar transposition. If the given ciphertext could not have resulted from columnar transposition with the given keyword, an AssertionError must be raised with the message invalid message. Otherwise the plaintext (str) must be returned.

Example

        >>> reduce('BANANARAMA')
'BANRM'
>>> reduce('overnumerousnesses')
'OVERNUMS'
>>> reduce('Mississippi')
'MISP'

>>> column_indexing('BANANARAMA')
(1, 0, 3, 4, 2)
>>> column_indexing('overnumerousnesses')
(3, 7, 0, 4, 2, 6, 1, 5)
>>> column_indexing('Mississippi')
(1, 0, 3, 2)

>>> column_order('BANANARAMA')
(1, 0, 4, 2, 3)
>>> column_order('overnumerousnesses')
(2, 6, 4, 0, 3, 7, 5, 1)
>>> column_order('Mississippi')
(1, 0, 3, 2)

>>> encode("It Ain't What You Do...", 'BANANARAMA')
"t'au.Inho.iWYo? tt .A  D?"
>>> encode("lacks ascenders, descenders, and dots in lower case", 'overnumerousnesses')
'cnesooeasnni ?sec se?lc e  akds,tw?s,ddnc? rea r?aedrdls'
>>> encode("One-Mississippi, two-Mississippi", 'Mississippi')
'nisptMipOMip -si-si,ossiessiwisp'

>>> decode("t'au.Inho.iWYo? tt .A  D?", 'BANANARAMA')
"It Ain't What You Do...??"
>>> decode('cnesooeasnni ?sec se?lc e  akds,tw?s,ddnc? rea r?aedrdls', 'overnumerousnesses')
'lacks ascenders, descenders, and dots in lower case?????'
>>> decode('nisptMipOMip -si-si,ossiessiwisp', 'Mississippi')
'One-Mississippi, two-Mississippi'

The first columnar transposition corresponds to the example from the introduction. For easier debugging, we also provide a graphical representation of the grids used by the two other columnar transpositions.

Encryption of the sentence lacks ascenders, descenders, and dots in lower case using columnar transposition with the keyword overnumerousnesses.

Encryption of the sentence One-Mississippi, two-Mississippi using columnar transposition with the keyword Mississippi.