A protein1 consists of a linear chain of amino acids2. In a process called protein folding3, the chain spontaneously folds into a native4 three-dimensional structure5 in which the protein is biologically active.
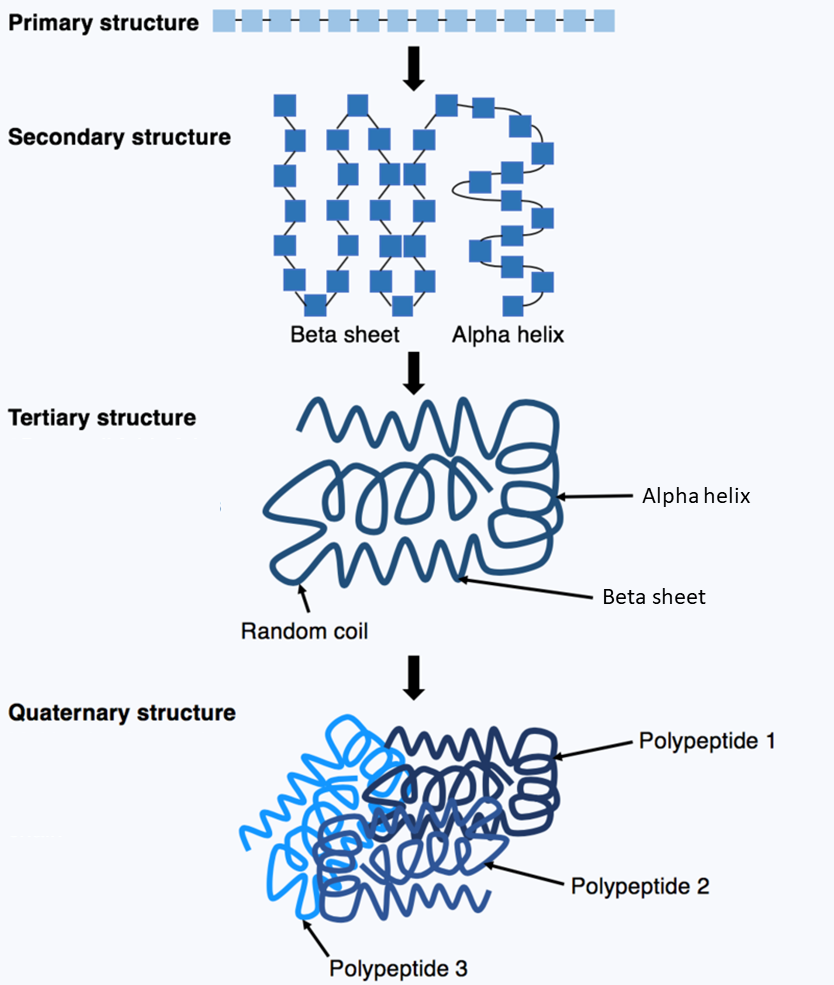
DNA sequences contain fundamental information about the sequences of these amino acids, but the information about the protein folding and structures are determined by physical processes which can not be directly predicted from the DNA sequences. To determine the target structures that proteins fold into, scientists look to experimental techniques such as X-ray crystallography6, cryo-electron microscopy7 and nuclear magnetic resonance8 which are both expensive and time-consuming.
Such efforts have identified the structures of about 170.000 proteins over the last 60 years, while there are over 200 million known proteins across life forms. There are numerous computational methods for protein structure prediction, but their accuracy has not been close to experimental techniques, thus limiting their value.
Until 2018, when the scientific world was astonished to see the accuracy achieved by AlphaFold9 in predicting protein structures. This artificial intelligence10 program developed by Google's Deepmind11 first takes a few weeks to learn from the 170.000 known protein structures how protein folding works, after which it takes a matter of days to make highly accurate predictions of unknown protein structures.
Assignment
The Protein Data Bank12 (PDB) is a freely accessible database for three-dimensional structural data of proteins (and other large biomolecules such as nucleic acids). The three-dimensional structures of proteins are described in the so-called PDB-format: a format for text files (with extension .pdb) that look like:
HEADER EXTRACELLULAR MATRIX 22-JAN-98 1A3I TITLE X-RAY CRYSTALLOGRAPHIC DETERMINATION OF A COLLAGEN-LIKE TITLE 2 PEPTIDE WITH THE REPEATING SEQUENCE (PRO-PRO-GLY) … EXPDTA X-RAY DIFFRACTION AUTHOR R.Z.KRAMER,L.VITAGLIANO,J.BELLA,R.BERISIO,L.MAZZARELLA, AUTHOR 2 B.BRODSKY,A.ZAGARI,H.M.BERMAN … REMARK 350 BIOMOLECULE: 1 REMARK 350 APPLY THE FOLLOWING TO CHAINS: A, B, C REMARK 350 BIOMT1 1 1.000000 0.000000 0.000000 0.00000 REMARK 350 BIOMT2 1 0.000000 1.000000 0.000000 0.00000 … SEQRES 1 A 9 PRO PRO GLY PRO PRO GLY PRO PRO GLY SEQRES 1 B 6 PRO PRO GLY PRO PRO GLY SEQRES 1 C 6 PRO PRO GLY PRO PRO GLY … ATOM 1 N PRO A 1 8.316 21.206 21.530 1.00 17.44 N ATOM 2 CA PRO A 1 7.608 20.729 20.336 1.00 17.44 C ATOM 3 C PRO A 1 8.487 20.707 19.092 1.00 17.44 C ATOM 4 O PRO A 1 9.466 21.457 19.005 1.00 17.44 O ATOM 5 CB PRO A 1 6.460 21.723 20.211 1.00 22.26 C … HETATM 130 C ACY 401 3.682 22.541 11.236 1.00 21.19 C HETATM 131 O ACY 401 2.807 23.097 10.553 1.00 21.19 O HETATM 132 OXT ACY 401 4.306 23.101 12.291 1.00 21.19 O …
Each line of a PDB-file has a specific type, indicated by the first six characters on the line (positions 1–6). What interests us here are the ATOM-lines (lines with type ATOM) that each describe one atom in the three-dimensional structure of the protein. Positions 31–38, 39–46 and 47–54 contain real numbers that indicate the three-dimensional coordinates of the atom in the protein structure (expressed in ångström13). We will represent such coordinates as a tuple $$(x, y, z)$$ of three real numbers (float). Positions 77–78 contain the symbolic representation of the atom. Each information field indicated by start and end positions may contain leading and/or trailing spaces. The following table summarizes the information in the ATOM-lines that we need for this assignment.
| characters | format | description |
|---|---|---|
| 1–6 | text | line type (in this case the text ATOM) |
| 31–38 | real number | $$x$$-coordinate of the atom |
| 39–46 | real number | $$y$$-coordinate of the atom |
| 47–54 | real number | $$z$$-coordinate of the atom |
| 77–78 | text | symbolic representation of the atom (uppercase) |
To compute some properties of protein structures, we also need the mass of the atoms. This can be retrieved from a text file that uses the following format:
atomic number symbol English Dutch atomic mass 1 H hydrogen waterstof 1.00794 2 He helium helium 4.002602 3 Li lithium lithium 6.941 4 Be beryllium beryllium 9.012182 5 B boron boor 10.811 6 C carbon koolstof 12.011 7 N nitrogen stikstof 14.00674 8 O oxygen zuurstof 15.9994 9 F fluorine fluor 18.9984 10 Ne neon neon 20.1797 …
The first line is a header (and may therefore be ignored). Each subsequent line describes an atom using five tab-separated fields: i) atomic number, ii) symbolic representation (corresponds to the last field of the ATOM-lines in a PDB-file), iii) English name, iv) Dutch name and v) atomic mass (a real number). Your task:
-
Write a function distance that takes two three-dimensional coordinates $$(x_1, y_1, z_1)$$ and $$(x_2, y_2, z_2)$$. The function must return the Euclidean distance between the two coordinates, which is computed as: \[ \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2} \]
-
Write a function read_atoms that takes the location (str) of a PDB-file. The function must return a list of the atoms from the PDB-file, listed in their order of appearance in the PDB-file. Each atom corresponds to an ATOM-line and is represented as a tuple with two elements: i) the symbolic representation of the atom (str; without leading and trailing spaces) and ii) the three-dimensional coordinates of the atom.
-
Write a function read_mass that takes the location (str) of a text file containing the mass of the atoms. The function must return a dictionary (dict) that maps the symbolic representation of each atom (str; in uppercase) onto its atomic mass (float).
-
Write a function protein_mass that takes the locations (str) of two text files: i) a PDB-file containing the three-dimensional structure of a protein and ii) a file containing the mass of the atoms. The function must return the total mass (float) of the protein. The total mass of a protein consisting of $$n$$ atoms with mass $$m_i$$ ($$1 \leq i \leq n$$) is computed as \[ \sum_{i=1}^{n}m_i \]
-
Write a function center_of_mass that takes the locations (str) of two text files: i) a PDB-file containing the three-dimensional structure of a protein and ii) a file containing the mass of the atoms. The function must return the center of mass of the protein. The center of mass of a protein consisting of $$n$$ atoms with mass $$m_i$$ ($$1 \leq i \leq n$$) and coordinates $$(x_i, y_i, z_i)$$ is a coordinate $$(x, y, z)$$ with \[ \, x = \dfrac{\displaystyle\sum_{i=1}^n m_i\,x_i}{\displaystyle\sum_{i=1}^n m_i} \qquad \, y = \dfrac{\displaystyle\sum_{i=1}^n m_i\,y_i}{\displaystyle\sum_{i=1}^n m_i} \qquad \, z = \dfrac{\displaystyle\sum_{i=1}^n m_i\,z_i}{\displaystyle\sum_{i=1}^n m_i} \]
Example
In the following interactive session we assume the text files mbs.pdb14 and periodic_table.txt15 to be located in the current directory.
>>> distance((15.74, 11.178, -11.733), (15.234, 10.462, -10.556))
1.4676583389876559
>>> atoms = read_atoms('mbs.pdb')
>>> len(atoms)
1223
>>> atoms[0]
('N', (15.74, 11.178, -11.733))
>>> atoms[1]
('C', (15.234, 10.462, -10.556))
>>> atoms[-1]
('O', (-11.704, -9.2, 0.489))
>>> mass = read_mass('periodic_table.txt')
>>> mass['H']
1.00794
>>> mass['O']
15.9994
>>> protein_mass('mbs.pdb', 'periodic_table.txt')
16036.10434000035
>>> center_of_mass('mbs.pdb', 'periodic_table.txt')
(13.77160318215512, -2.956867920527567, 7.905965346916511)