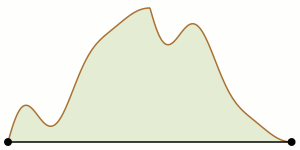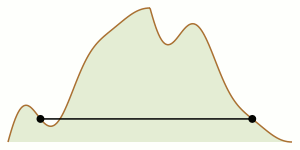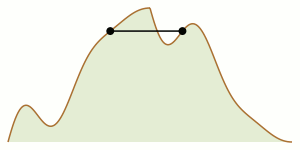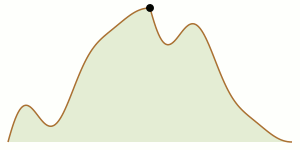
Twee bergbeklimmers starten aan weerszijden van een bergtop. Kunnen ze samen de bergtop bereiken als ze zich op hun tocht altijd op dezelfde hoogte van elkaar moeten bevinden?
Het profiel van een (tweedimensionale) berg wordt voorgesteld door een reeks (list of tuple) natuurlijk getallen (int) die de hoogtes van de lokale pieken en dalen voorstellen. Daarbij moeten de volgende voorwaarden gelden:
-
de twee bergbeklimmers moeten per definitie op dezelfde hoogte starten, en dus moet het eerste getal (starthoogte van de bergbeklimmer die links start) gelijk zijn aan het laatste getal (starthoogte van de bergbeklimmer die rechts start)
-
er is geen enkel punt langs het profiel dat lager ligt dan de starthoogte van de twee bergbeklimmers
-
er is slechts één punt langs het profiel waarop de maximale hoogte bereikt wordt (de top van de berg)
-
het profiel bestaat achtereenvolgens uit pieken en dalen; elk getal moet dus alternerend groter of kleiner zijn dan het voorgaande getal uit de reeks
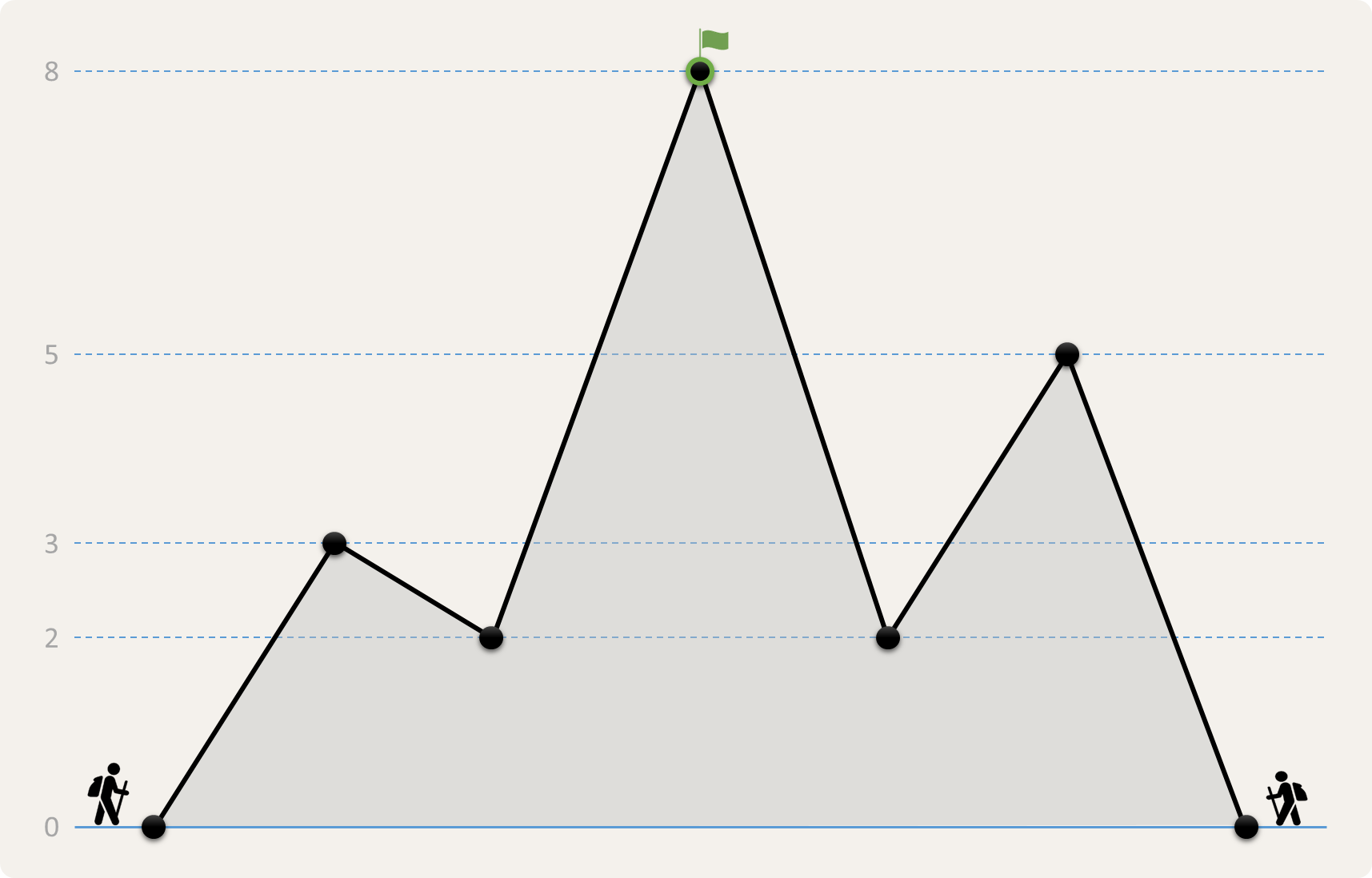
Er bestaat altijd minstens één manier waarop de bergbeklimmers samen de top kunnen bereiken van een berg waarvan het profiel aan deze voorwaarden voldoet. Hieronder zie je bijvoorbeeld de grafische voorstelling van een berg met profiel [0, 3, 2, 8, 3, 5, 0], waarbij de lokale pieken en dalen worden aangeduid door zwarte stippen. Op de top hebben we een groene vlag geplant en hebben we de zwarte stip een groene rand gegeven. Aan de linkerkant worden de hoogtes van de lokale pieken en dalen in het lichtgrijs weergegeven, met blauwe horizontale hoogtelijnen die aangeven welke punten op dezelfde hoogte liggen als de pieken en dalen.
De mogelijke routes die de bergbeklimmers kunnen volgen, kunnen gevonden worden door een verbindingsgraaf op te stellen voor het profiel. Ter herinnering: een graaf is een datastructuur $$G = (K, B)$$ die bestaat uit een verzameling knopen $$K$$ en een verzameling bogen $$B$$ die telkens twee knopen met elkaar verbinden.
Een verbindingsgraaf is een graaf waarvan elke knoop bestaat uit een koppel punten $$(P_L, P_R)$$ die zich op dezelfde hoogte bevinden. Daarbij geldt ook nog dat $$P_L$$ zich links van de top bevindt en $$P_R$$ rechts van de top, en dat minstens één van beide punten een lokale piek of een lokaal dal is (het andere punt mag ook een lokale piek of een lokaal dal zijn). Twee knopen $$(P_L, P_R)$$ en $$(P'_L, P'_R)$$ van een verbindingsgraaf worden met elkaar verbonden als en slechts als de twee bergbeklimmers zich in dezelfde richting (beide naar boven of beide naar onder) kunnen begeven, respectievelijk van $$P_L$$ naar $$P'_L$$ en van $$P_R$$ naar $$P'_R$$.
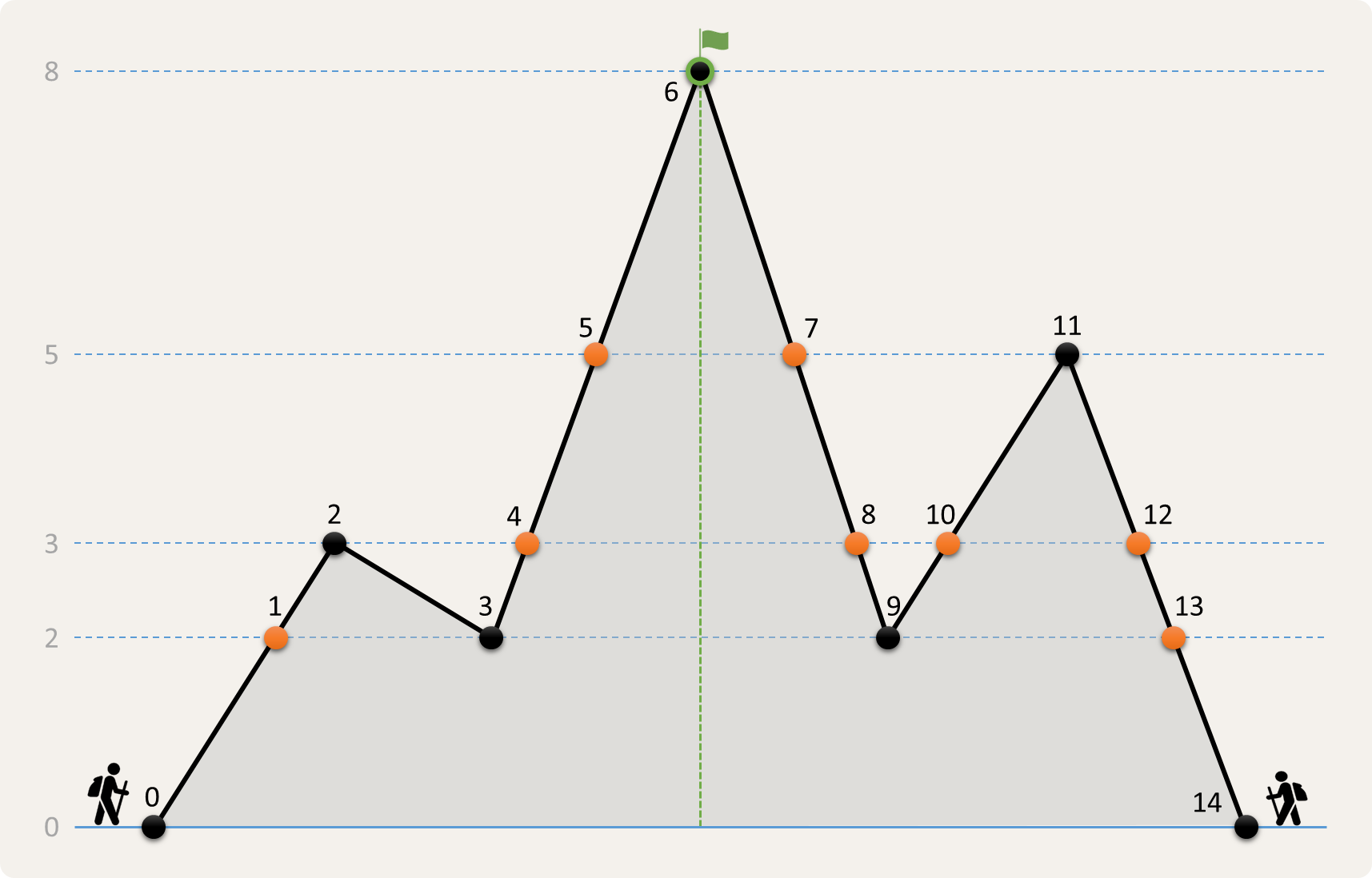
Om de verbindingsgraaf op te stellen, bepalen we eerst alle punten langs het profiel die zich op dezelfde hoogte bevinden als een lokale piek of een lokaal dal van het profiel. Dit zijn uiteraard de pieken en dalen zelf, maar ook enkele bijkomende punten tussen de pieken en dalen die we in bovenstaande afbeelding hebben aangeduid in het oranje. Deze punten worden van links naar rechts genummerd vanaf nul. Als de linkse klimmer zich bijvoorbeeld op punt 2 bevindt, dan kan de rechtse klimmer zich op punt 8, 10 of 12 bevinden. De koppels $$(2, 8)$$, $$(2, 10)$$ en $$(2, 12)$$ zijn dus knopen van de verbindingsgraaf, omdat de bergbeklimmers zich op een bepaald moment op deze punten kunnen bevinden. Hieronder hebben we ook de bogen getekend tussen de knopen van de verbindingsgraaf voor een berg met profiel [0, 3, 2, 8, 3, 5, 0].
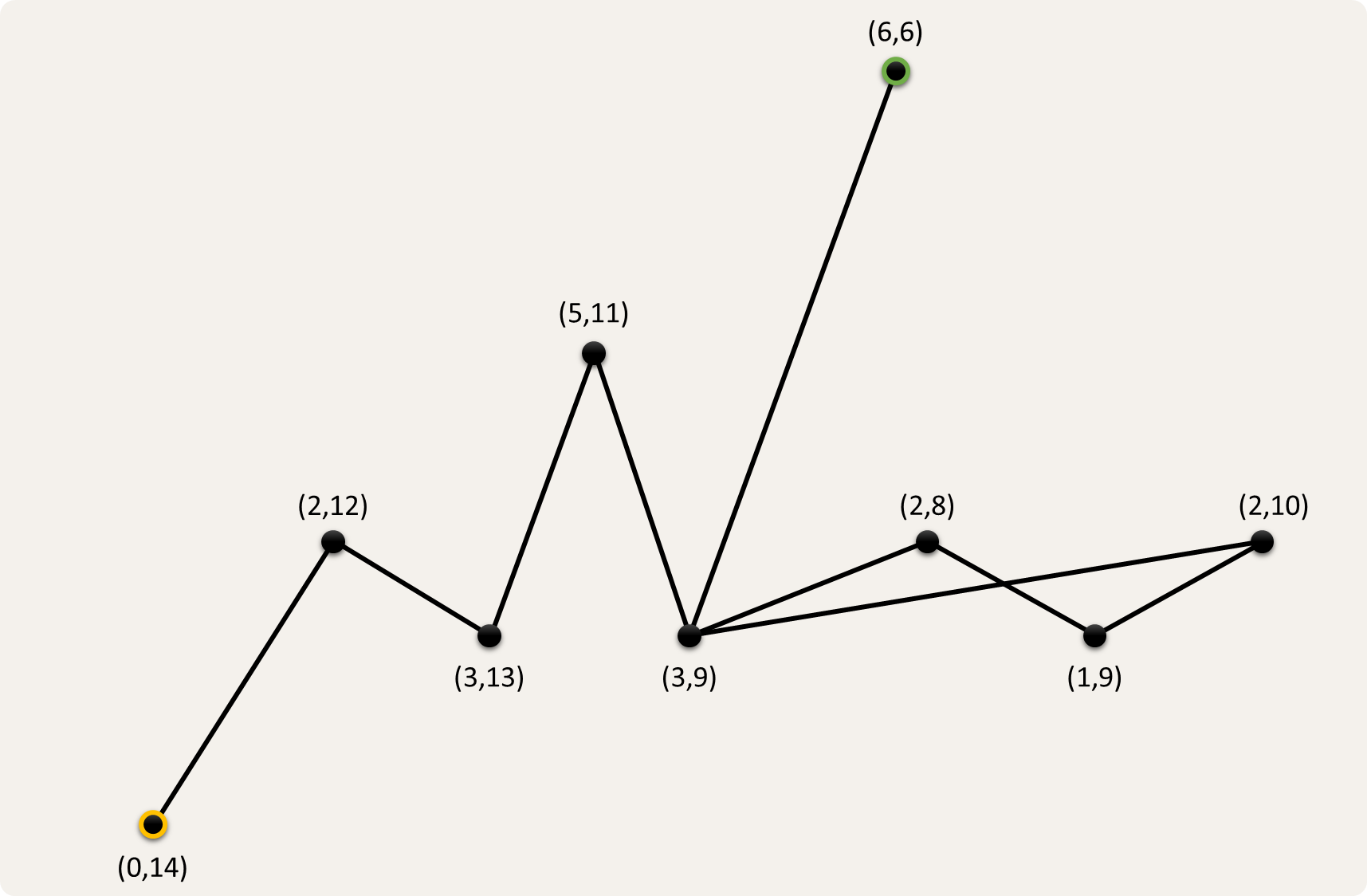
Rest ons nu nog de vraag of er in de verbindingsgraaf een pad kan gevonden worden tussen de startknoop $$(0, 14)$$ waarin de twee bergbeklimmer zich aan de voet van de berg bevinden (aangeduid met een oranje rand) en de knoop $$(6, 6)$$ die de top aanduidt waar de twee klimmers samenkomen (aangeduid met een groene rand). Voor de verbindingsgraaf hierboven is het antwoord duidelijk ja. Als we het pad volgen van $$(0, 14)$$ naar $$(6, 6)$$, dan zien we dat beide bergbeklimmers eerst stijgen naar de eerste piek $$(2, 12)$$, waarna de linkse bergbeklimmer verder afdaalt richting de top, terwijl de rechtse bergbeklimmer op zijn stappen terugkeert totdat ze op $$(3, 13)$$ uitkomen. Daarna stijgen beide bergbeklimmers naar $$(5, 11)$$, waarna de linkse bergbeklimmer op zijn stappen terugkeert en de rechtse bergbeklimmer verder stijgt richting de top, totdat ze op $$(3, 9)$$ uitkomen. Van daaruit kunnen de twee bergbeklimmers samen de laatste klim naar de top inzetten, om op $$(6, 6)$$ uit te komen.
Opgave
Bepaal de verbindingsgraaf voor een gegeven bergprofiel. Hiervoor ga je als volgt te werk:
-
Schrijf een functie is_profiel waaraan een reeks (list of tuple) van natuurlijke getallen (int) moet doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of de gegeven reeks voldoet aan de voorwaarden die moeten gelden voor een profiel.
-
Schrijf een functie piek waaraan een bergprofiel moet doorgegeven worden. De functie moet de hoogte (int) van de bergtop teruggeven.
-
Schrijf een functie niveaus waaraan een bergprofiel moet doorgegeven worden. De functie moet een lijst (list) met de hoogtes (int) van de pieken en dalen van het profiel teruggeven. Daarin komt elke hoogte slechts één keer voor, en worden de hoogtes in stijgende volgorde opgelijst.
-
Schrijf een functie tussenpunten waaraan een bergprofiel moet doorgegeven worden. De functie moet een lijst (list) teruggeven met alle punten langs het profiel die zich op dezelfde hoogte bevinden als een lokale piek of een lokaal dal van het profiel. Hierbij wordt elk punt voorgesteld door een tuple $$(h, b)$$, waarbij $$h$$ de hoogte (int) van het punt aangeeft en $$b$$ een Booleaanse waarde (bool) is die aangeeft of het punt een lokale piek of een lokaal dal is. De punten moeten van links naar rechts opgelijst worden.
-
Schrijf een functie hoogtelijnen waaraan een bergprofiel moet doorgegeven worden. De functie moet een dictionary (dict) teruggeven, waarvan de sleutels gevormd worden door de hoogtes (int) van alle pieken en dalen langs het profiel. Elke hoogte $$h$$ moet afgebeeld worden op een tuple met twee elementen: i) de verzameling (set) van alle punten op hoogte $$h$$ langs het profiel die zich niet aan de rechterkant van de top bevinden (dus inclusief de top zelf) en ii) de verzameling (set) van alle punten op hoogte $$h$$ langs het profiel die zich niet aan de linkerkant van de top bevinden (dus inclusief de top zelf). Alle punten uit deze dictionary worden voorgesteld door een tuple $$(i, b)$$, waarbij $$i$$ het volgnummer van het punt is (zie inleiding voor links-rechts nummering van de punten) en $$b$$ een Booleaanse waarde (bool) is die aangeeft of het punt een lokale piek of een lokaal dal is.
-
Schrijf een functie knopen waaraan een bergprofiel moet doorgegeven worden. De functie moet een verzameling (set) teruggeven met alle knopen in de verbindingsgraaf van het gegeven bergprofiel. Hierbij worden de punten in de knopen voorgesteld door hun volgnummer (zie inleiding voor links-rechts nummering van de punten).
-
Schrijf een functie zijn_verbonden waaraan drie argumenten moeten doorgegeven worden: twee knopen $$(P_L, P_R)$$ en $$(P'_L, P'_R)$$ in de verbindingsgraaf van een bergprofiel en het bergprofiel zelf. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of de knopen $$(P_L, P_R)$$ en $$(P'_L, P'_R)$$ met elkaar verbonden zijn in de verbindingsgraaf van het gegeven profiel.
Bogen van verbindingsgraaf
Twee knopen $$(P_L, P_R)$$ en $$(P'_L, P'_R)$$ van een verbindingsgraaf zijn met elkaar verbonden als en slechts als de volgende voorwaarden voldaan zijn:
-
de twee bergbeklimmers lopen over dezelfde heuvelrug van de ene knoop naar de andere knoop; er liggen met andere woorden geen lokale pieken of dalen tussen $$P_L$$ en $$P'_L$$ liggen, en ook niet tussen $$P_R$$ en $$P'_R$$
-
de twee bergbeklimmers stappen in dezelfde richting (naar boven of naar beneden) van $$P_L$$ naar $$P'_L$$ en van $$P_R$$ naar $$P'_R$$; met andere woorden $$P_L - P'_L$$ en $$P_R - P'_R$$ hebben hetzelfde teken
-
-
Schrijf een functie verbindingsgraaf waaraan een bergprofiel moet doorgegeven worden. De functie moet een dictionary (dict) teruggeven, die elke knoop uit de verbindingsgraaf van het gegeven bergprofiel afbeeldt op de verzameling (set) knopen waarmee die knoop verbonden is in de verbindingsgraaf.
Voorbeeld
>>> profiel = [0, 3, 2, 8, 2, 5, 0]
>>> is_profiel(profiel)
True
>>> piek(profiel)
8
>>> niveaus(profiel)
[0, 2, 3, 5, 8]
>>> tussenpunten(profiel)
[(0, True), (2, False), (3, True), (2, True), (3, False), (5, False), (8, True), (5, False), (3, False), (2, True), (3, False), (5, True), (3, False), (2, False), (0, True)]
>>> hoogtelijnen(profiel)
{0: ({(0, True)}, {(14, True)}), 2: ({(1, False), (3, True)}, {(9, True), (13, False)}), 3: ({(2, True), (4, False)}, {(10, False), (8, False), (12, False)}), 5: ({(5, False)}, {(11, True), (7, False)}), 8: ({(6, True)}, {(6, True)})}
>>> knopen(profiel)
{(3, 13), (5, 11), (0, 14), (2, 8), (6, 6), (2, 10), (3, 9), (1, 9), (2, 12)}
>>> zijn_verbonden((0, 14), (2, 12), profiel)
True
>>> zijn_verbonden((2, 12), (0, 14), profiel)
True
>>> zijn_verbonden((5, 11), (2, 8), profiel)
False
>>> verbindingsgraaf(profiel)
{(3, 13): {(2, 12), (5, 11)}, (5, 11): {(3, 9), (3, 13)}, (2, 12): {(0, 14), (3, 13)}, (3, 9): {(6, 6), (2, 8), (2, 10), (5, 11)}, (0, 14): {(2, 12)}, (2, 8): {(3, 9), (1, 9)}, (1, 9): {(2, 8), (2, 10)}, (6, 6): {(3, 9)}, (2, 10): {(3, 9), (1, 9)}}
>>> is_profiel([0, 3, 2, 8, 2, 5, 2])
False
>>> is_profiel([0, 3, 2, 8, 2, 8, 0])
False
>>> is_profiel([1, 3, 0, 8, 2, 5, 1])
False
>>> is_profiel([0, 3, 5, 8, 2, 5, 0])
False