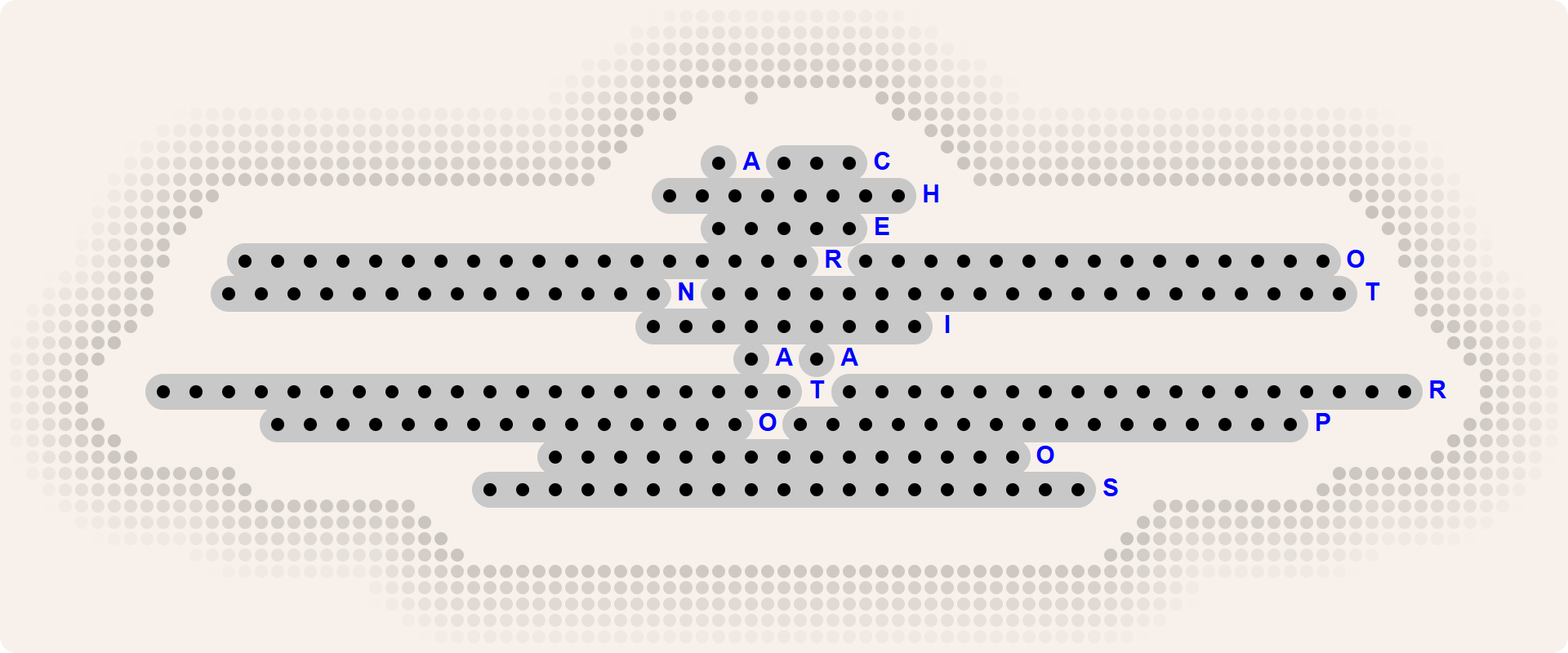
Wat zie je in deze inktvlek?

Wat zie je in deze inktvlek?

Antwoord weergeven

Als je een of ander gevleugeld insect meent te herkennen, dan is onze codering in haar opzet geslaagd. De breedte van een ononderbroken horizontale lijn (hieronder aangeduid door een reeks opeenvolgende zwarte cirkels) komt overeen met een letter: A=1, B=2, C=3, …. De bovenste horizontale lijn bevat 20 zwarte cirkels en staat dus voor de letter T als de twintigste letter van het alfabet. Daaronder staat een lijn met 18 zwarte cirkels die staat voor de letter R. De lijn daaronder wordt twee keer onderbroken en bestaat dus uit drie reeksen: een reeks van 15 zwarte cirkels (de letter O), een reeks van 7 zwarte cirkels (de letter G), en nog een reeks van 15 zwarte cirkels (de letter O).

De inktvlek is een versleuteling van TROGONOPTERABROOKIANA op basis van de Leptidoptera-codering. Rajah Brooke's vogelvleugel (Trogonoptera brookiana) is een vlinder die in 1855 door Alfred Russel Wallace werd vernoemd naar Sir James Brooke¹, die bekend staat als de eerste blanke radja van Sarawak². Het is de nationale vlinder van Maleisië. De Rorschachtest³-achtige inktvlek is dus een vlinder gecodeerd als een vlinder.

Als we de letters voor alle reeksen achter elkaar zetten, dan krijgen we TROGONOPTERABROOKIANA. Rajah Brooke's vogelvleugel (Trogonoptera brookiana) is een vlinder die in 1855 door Alfred Russel Wallace werd vernoemd naar Sir James Brooke⁴, die bekend staat als de eerste blanke radja van Sarawak⁵. Het is de nationale vlinder van Maleisië. De Rorschachtest⁶-achtige inktvlek was dus een vlinder gecodeerd als een vlinder.

Trogonoptera brookiana

Opgave

We gebruiken de Leptidoptera-codering om een klare tekst die enkel bestaat uit letters (hoofdletters en kleine letters) en spaties te versleuten als een tekstbestand waarvan de inhoud er met een beetje verbeelding uitziet als een zwart-wit afbeelding van een vlinder, een mot of een ander geveugeld insect. In de cijfertekst (de inhoud van het tekstbestand) worden twee karakters gebruikt: een karakter die een donkere kleur (zwart) voorstelt en een karakter die een lichte kleur (wit) voorstelt. De klare tekst wordt op de volgende manier versleuteld:

Een letter die op positie $$n$$ staat in het alfabet (A=1, B=2, C=3, …) wordt gecodeerd als $$n$$ herhalingen van het donker karakter. Daarbij wordt geen onderscheid gemaakt tussen hoofdletters en kleine letters.
Een groep letters is een zo lang mogelijke reeks opeenvolgende letters in de klare tekst die niet onderbroken wordt door spaties. Een groep letters wordt gecodeerd door de individuele letters van de groep te coderen, en die coderingen telkens van elkaar te scheiden door één licht karakter.
De regels van het tekstbestand worden gevormd door de coderingen van de opeenvolgende groepen letters in de klare tekst. Elke regel bevat evenveel karakters. Dit aantal $$m$$ is gelijk aan het aantal karakters in de langste codering van een groep letters in de klare tekst. Als de codering van een groep letters uit minder dan $$m$$ karakters bestaat, dan wordt die vooraan en achteraan gelijkmatig aangevuld met lichte karakters. Als er een oneven aantal karakters moet aangevuld worden, dan wordt er achteraan één licht karakter meer aangevuld dan vooraan.

Stel bijvoorbeeld dat we deze klare tekst

T r ogo nop ter a b r oo k i ana

willen versleutelen met een hekje (#) als donkere kleur en een koppelteken (-) als lichte kleur. De klare tekst telt in totaal 12 lettergroepen. De eerste lettergroep T wordt gecodeerd als 20 hekjes.

####################

De tweede lettergroep r wordt gecodeerd als 18 hekjes.

##################

De derde lettergroep ogo wordt gecodeerd als 15 hekjes (de letter o is de vijftiende letter van het alfabet) gevolgd door een koppelteken, 7 hekjes, een koppelteken, en nog eens 15 hekjes.

###############-#######-###############

De vierde lettergroep nop wordt gecodeerd als 14 hekjes gevolgd door een koppelteken, 15 hekjes, een koppelteken, en 16 hekjes.

##############-###############-################

Met 47 karakters is dit meteen de langste codering van alle lettergroepen in de klare tekst (we kunnen dit pas weten alles we alle lettergroepen gecodeerd hebben, maar neem het maar van ons aan). Daarmee hebben we meteen ook de vierde regel van het tekstbestand bepaald.

Omdat de codering van de eerste lettergroep nog maar uit 20 karakters bestaat, moeten we die aanvullen met 27 koppeltekens om de eerste regel te krijgen die in totaal ook 47 karakters bevat. We vullen de codering van de eerste lettergroep dus vooraan aan met 13 koppeltekens en achteraan met 14 koppeltekens.

-------------####################--------------

Als we de coderingen van alle 12 lettergroepen op dezelfde manier aanvullen tot 47 karakters, dan krijgt het tekstbestand deze versleutelde cijfertekst van 12 regels als inhoud (vlinder.01.txt⁷):

-------------####################--------------
--------------##################---------------
----###############-#######-###############----
##############-###############-################
-####################-#####-##################-
-----------------------#-----------------------
----------------------##-----------------------
--------------##################---------------
--------###############-###############--------
------------------###########------------------
-------------------#########-------------------
--------------#-##############-#---------------

Gevraagd wordt:

Schrijf een functie decodeer waaraan de locatie (str) moet doorgegeven worden van een tekstbestand dat een cijfertekst bevat die gecodeerd werd volgens de Leptidoptera-codering. De functie heeft een tweede optionele parameter donker waaraan het karakter (str) voor de donkere kleur kan doorgegeven worden (standaard wordt een hekje (#) als donkere kleur gebruikt). De functie heeft een derde optionele parameter licht waaraan het karakter (str) voor de lichte kleur kan doorgegeven worden (standaard wordt een spatie als lichte kleur gebruikt). De functie moet de reeks letters (str; in hoofdletters) teruggeven die corresponderen met de reeksen opeenvolgende donkere karakters in het bestand.
Schrijf een functie codeer_groep waaraan een groep letters (str) moet doorgegeven worden. De functie heeft een tweede optionele parameter donker waaraan het karakter (str) voor de donkere kleur kan doorgegeven worden (standaard wordt een hekje (#) als donkere kleur gebruikt). De functie heeft een derde optionele parameter licht waaraan het karakter (str) voor de lichte kleur kan doorgegeven worden (standaard wordt een spatie als lichte kleur gebruikt). De functie moet de versleuteling van de groep letters teruggeven volgens de Leptidoptera-codering.
Schrijf een functie codeer_groepen waaraan een klare tekst (str) moet doorgegeven worden die enkel bestaat uit letters (hoofdletters en kleine letters) en spaties. De functie heeft een tweede optionele parameter donker waaraan het karakter (str) voor de donkere kleur kan doorgegeven worden (standaard wordt een hekje (#) als donkere kleur gebruikt). De functie heeft een derde optionele parameter licht waaraan het karakter (str) voor de lichte kleur kan doorgegeven worden (standaard wordt een spatie als lichte kleur gebruikt). De functie moet een lijst (list) teruggeven met versleutelingen van de opeenvolgende groepen letters in de klare tekst volgens de Leptidoptera-codering.
Schrijf een functie aanvullen waaraan een string $$s$$ (str) moet doorgegeven worden. De functie heeft een tweede optionele parameter breedte waaraan een getal $$m \in \mathbb{N}$$ kan doorgegeven worden. De functie heeft een derde optionele parameter karakter waaraan een karakter (str) kan doorgegeven worden (standaard wordt een spatie als karakter gebruikt). Als er niet expliciet een argument wordt doorgegeven aan de parameter breedte of als de string $$s$$ minstens $$m$$ karakters bevat, dan moet de string $$s$$ zelf teruggegeven worden. Anders moet de string $$s$$ teruggegeven worden die vooraan en achteraan gelijkmatig aangevuld werd met karakters tot een string van $$m$$ karakters. Als er daarbij een oneven aantal karakters moeten aangevuld worden, dan wordt er achteraan één karakter meer aangevuld dan vooraan.
Schrijf een functie codeer waaraan een klare tekst (str) moet doorgegeven worden die enkel bestaat uit letters (hoofdletters en kleine letters) en spaties. De functie heeft een tweede optionele parameter donker waaraan het karakter (str) voor de donkere kleur kan doorgegeven worden (standaard wordt een hekje (#) als donkere kleur gebruikt). De functie heeft een derde optionele parameter licht waaraan het karakter (str) voor de lichte kleur kan doorgegeven worden (standaard wordt een spatie als lichte kleur gebruikt). De functie heeft een vierde optionele parameter bestand waaraan de locatie (str) van een tekstbestand kan doorgegeven worden. De functie moet de versleuteling van de klare tekst volgens de Leptidoptera-codering wegschrijven naar het bestand (vierde argument). Als er niet expliciet een bestandslocatie wordt doorgegeven aan de parameter bestand, dan moet de functie de versleuteling van de klare tekst uitschrijven.

Voorbeeld

In deze interactieve sessie gaan we ervan uit dat de tekstbestanden vlinder.01.txt⁸ en vlinder.02.txt⁹ zich in de huidige directory bevinden.

        >>> decodeer('vlinder.01.txt10', licht='-')
'TROGONOPTERABROOKIANA'
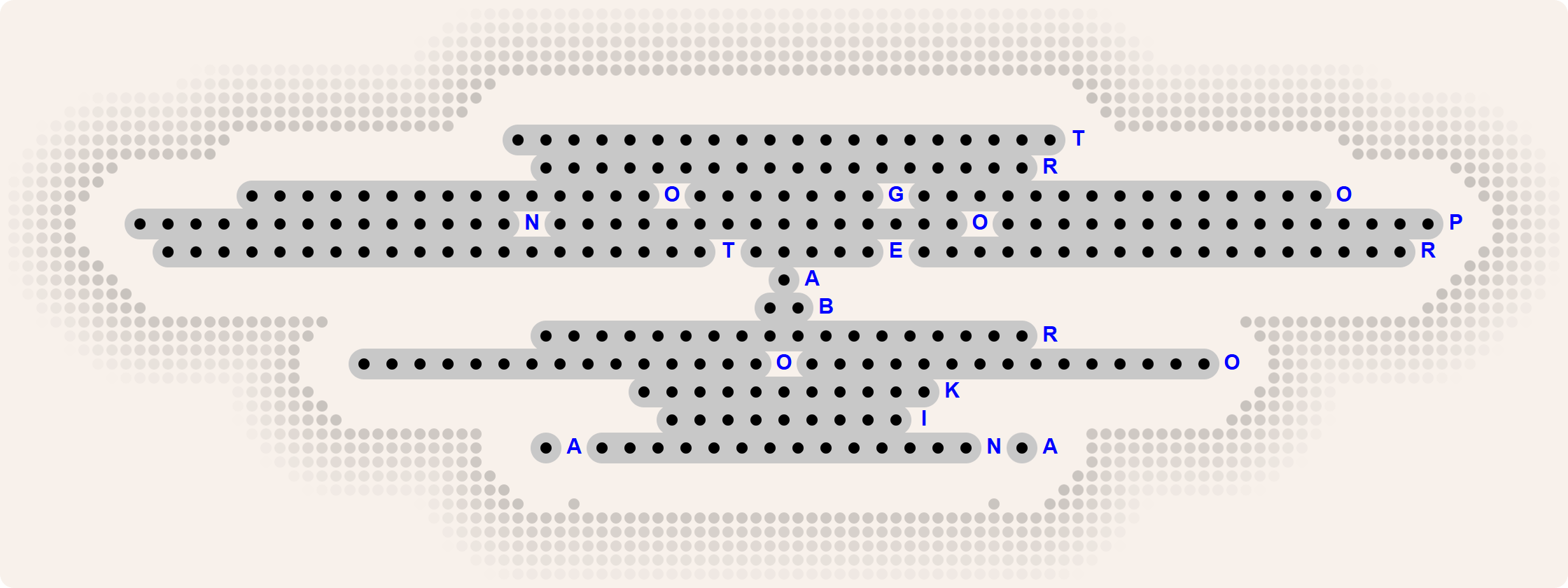
>>> decodeer('vlinder.02.txt11', donker='X', licht='_')
'ACHERONTIAATROPOS'

>>> codeer_groep('A')
'#'
>>> codeer_groep('BC', donker='X')
'XX XXX'
>>> codeer_groep('DEF', donker='@', licht='_')
'@@@@_@@@@@_@@@@@@'
>>> codeer_groep('GHIJ', licht='1', donker='8')
'8888888188888888188888888818888888888'

>>> codeer_groepen('A BC')
['#', '## ###']
>>> codeer_groepen('DEF GHIJ', donker='X')
['XXXX XXXXX XXXXXX', 'XXXXXXX XXXXXXXX XXXXXXXXX XXXXXXXXXX']
>>> codeer_groepen(' a  bc   def    ', donker='@', licht='_')
['@', '@@_@@@', '@@@@_@@@@@_@@@@@@']

>>> aanvullen('spam')
'spam'
>>> aanvullen('eggs', breedte=10)
'   eggs   '
>>> aanvullen('bacon', breedte=10, karakter='_')
'__bacon___'

>>> codeer('AAAAAA BBBB CCC')
# # # # # #
## ## ## ##
### ### ###
>>> codeer('  aaa  bbb  ccc  ', licht='_')
___#_#_#___
_##_##_##__
###_###_###
>>> codeer('GH IJK LM', donker='@', licht='-')
--------@@@@@@@-@@@@@@@@--------
@@@@@@@@@-@@@@@@@@@@-@@@@@@@@@@@
---@@@@@@@@@@@@-@@@@@@@@@@@@@---
>>> codeer('T r ogo nop ter a b r oo k i ana', licht='-')
-------------####################--------------
--------------##################---------------
----###############-#######-###############----
##############-###############-################
-####################-#####-##################-
-----------------------#-----------------------
----------------------##-----------------------
--------------##################---------------
--------###############-###############--------
------------------###########------------------
-------------------#########-------------------
--------------#-##############-#---------------
>>> codeer('Ac h e ro nt i aa tr op o s', donker='X', licht='_', bestand='cijfertekst.02.txt12')

Het bestand vlinder.01.txt¹³ correspondeert met de puzzel uit de inleiding van deze opgave. Het bestand vlinder.02.txt¹⁴ correspondeert met deze puzzel. Klik hier om de oplossing te bekijken.

Wat zie je in deze inktvlek?

Opgave

Voorbeeld

Epiloog