Het bijzondere aan willekeurigheid is dat het bestaan ervan nog niet is bewezen — maar ook nog door niemand kon weerlegd worden — ondanks het feit dat we er elke dag mee geconfronteerd worden in de wetenschap en in ons dagelijkse leven. Neem bijvoorbeeld de constante $$\pi$$: dit getal heeft een oneindig aantal cijfers na de komma, zonder dat de reeks een herkenbaar patroon vertoont. Toch blijken de 10 mogelijke cijfers vrij uniform verdeeld te zijn over de reeks — tenminste als we een visuele voorstelling maken van bijvoorbeeld de eerste miljoen cijfers na de komma.

Het opbouwen van een dergelijke visuele voorstelling gebeurt vrij eenvoudig. We starten in de oorsprong $$(0, 0)$$. Daarna lopen we de cijfers van het getal af van links naar rechts. Voor elk cijfer $$c$$ draaien we ons in wijzerzin over een hoek van $$c \times 36°$$ ten opzichte van de positieve Y-as en zetten daarna een stap van lengte één vooruit. Dit wordt geïllustreerd in onderstaande figuur voor de eerste tien cijfers van het getal $$\pi$$.
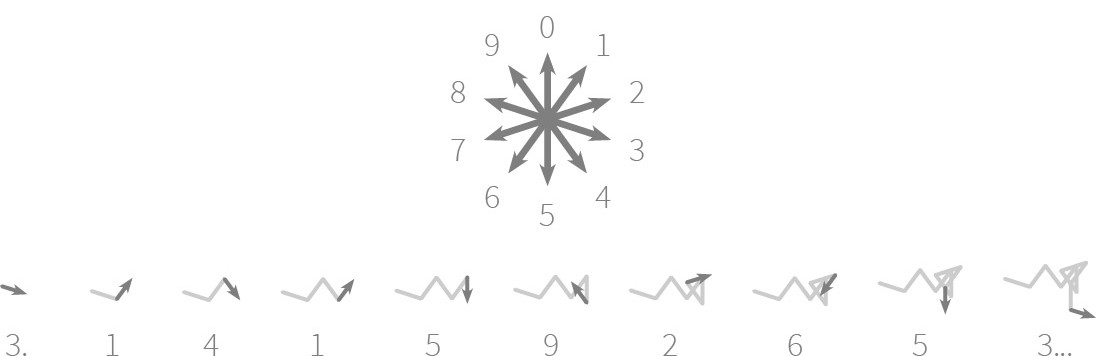
Voorstellingen van dit soort dronkenmanswandelingen zijn interessant voor mensen die meer inzicht willen krijgen in de mystieke eigenschappen van willekeurigheid en de onzichtbare krachten die eraan ten grondslag liggen. Ze zagen voor het eerst het levenslicht in 2009 in de masterthesis van Daniel A. Becker1, en werden later verfijnd in het Art in Pi2 project van Nadieh Bremer en het Number Walks3 project van Nicholas Rougeux. Het werk van deze laatste artiest met een aantal bekende wiskundige constanten en irrationale getallen zoals $$\pi$$, $$e$$ en de gouden snede werd gebundeld in onderstaande reeks videofragmenten.
Invoer
Eén regel tekst.
Uitvoer
De tekst Getal g wandelt naar positie (x, y)., waarbij g moet ingevuld worden met de tekst uit de invoer, en x en y moeten ingevuld worden met de $$(x, y)$$-coördinaten waar men eindigt, als men start in de oorsprong, alle cijfers van de gegeven tekst van links naar rechts afloopt, en voor elk cijfer een stap van lengte één zet in de richting die omschreven wordt in de inleiding. Hierbij moeten de coördinaten uitgeschreven worden met twee cijfers na de komma.
Voorbeeld
Invoer:
3.141592653Uitvoer:
Getal 3.141592653 wandelt naar positie (3.44, -1.50).Epiloog: Feynmanpunt
In de decimale voorstelling van het getal $$\pi$$ komt een reeks van zes opeenvolgende negens voor die begint bij het 762ste cijfer na de komma. Deze reeks is beroemd geworden omwille van het wiskundige toeval en omwille van de idee dat men het getal $$\pi$$ van buiten zou kunnen leren tot op dit punt, zodat men de cijfers daarna één voor één zou kunnen debiteren en eindigen met "negen negen negen negen negen negen enzoverder", waardoor de indruk gewekt wordt dat $$\pi$$ een rationaal getal is. De oudste gekende vermelding van dit idee staat in het boek Metamagical Themas van Douglas Hofstadter uit 1985, waarin Hofstadter zegt
I myself once learned 380 digits of $$\pi$$, when I was a crazy high-school kid. My never-attained ambition was to reach the spot, 762 digits out in the decimal expansion, where it goes "999999", so that I could recite it out loud, come to those six 9's, and then impishly say, "and so on!"
De reeks van zes opeenvolgende negens wordt vaak het Feynmanpunt genoemd. Het werd vernoemd naar de fysicus Richard Feynman die ook ooit eens tijdens een zou hebben gezegd dat hij de cijfers van de decimale ontwikkeling van $$\pi$$ tot dat punt wilde van buiten leren. Het is echter niet duidelijk wanneer, en zelfs of, Feynman dit zou gezegd hebben. Het wordt nergens expliciet vermeld in gepubliceerde biografieën noch in zijn autobiografie, en de waarheid van dit feit kon ook niet bevestigd worden door zijn biograaf James Gleick.
