Een Euleriaans circuit in een Euleriaanse graaf (i.e. een graaf waarin het aantal inkomende bogen gelijk is aan het aantal uitgaande voor elke top) is een cykel die alle bogen van de graaf bevat. Er moet dus met andere woorden een pad bepaald worden in de graaf die elke boog precies eenmaal aandoet en start en eindigt in dezelfde top.

Een Euleriaans circuit in een graaf is niet uniek. Zo is het circuit afhankelijk van de starttop, en kan er onderweg een andere boog worden gekozen om eerst aan te doen. Bij de implementatie van dit algoritme is het voldoende dat je één van de Euleriaanse cykels geeft.

Voorbeeld

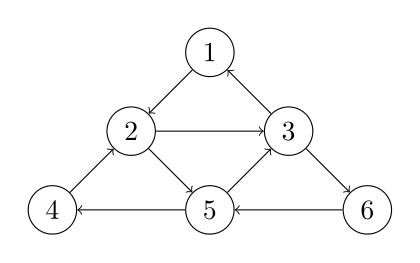
Bovenstaande graaf is Euleriaans: het aantal inkomende bogen is in elke top gelijk aan het aantal uitgaande bogen. We kunnen in deze graaf dus een Euleriaans circuit bepalen. We nemen als starttop voor ons circuit een willekeurige top, bijvoorbeeld 1. Een mogelijk Euleriaans circuit in de graaf is dan gegeven door [1, 2, 3, 6, 5, 4, 2, 5, 3, 1]. Merk op dat ook [1, 2, 5, 3, 6, 5, 4, 2, 3, 1] een Euleriaans circuit is met starttop 1.

Het bepalen van een Euleriaans circuit kan op de volgende manier gebeuren:

// find start of eulerian cycle
start = random node
// initialize eulerian cycle with start node
euler = [start]
// initialize set of nodes in current cycle with more unused outgoing edges
nodes = {start}
// continue until all edges have been included in the cycle
while (nodes not empty) {
  // take any node v in current cycle with unused outgoing edges
  v = nodes.iterator().next()
  // initialize empty walk
  walk = []
  // add nodes to walk
  u = v
  while (node u has unused outgoing edges) {
    // take next unused outgoing edge
    e = next unused outgoing edge from u
    // check if all edges are used now
    if(u has no more unused edges){
      nodes.remove(u)
    }
    // move to destination of edge and add to walk
    u = e.destination
    walk.add(u)
    // add u to queue if it has unused outgoing edges
    if(u has unused edges){
      nodes.add(u)
    }
  }
  // insert new walk from v in eulerian cycle
  euler.insert(v, walk)
}

Implementeer dit algoritme in een methode public Walk<String> createCircuit(DirectedMultiGraph<String> graph) in een klasse EulerianCycle. Deze klasse is een implementatie van de interface Cycle¹.

De methode createCircuit neemt als input een graaf van het type DirectedMultiGraph<String> en geeft als output een object van de klasse Walk<String> terug. Dit object bevat de bezochte toppen, in juiste volgorde, van het Euleriaans circuit.

In deze oefening maken we gebruik van een kleine grafenbibliotheek graphlib² die o.a. de klassen DirectedMultiGraph en Walk bevat. De volledige API kan je hier³ raadplegen. Andere interessante klassen die je zeker nodig zal hebben in je implementatie zijn Node en DirectedEdge. Neem eerst en vooral eens de API door en stel eventueel vragen hierover voor je begint te programmeren.

Belangrijke opmerking: om met de grafenbibliotheek te kunnen werken in IntelliJ, moet je het bestand graphlib.jar⁴ toevoegen aan je project. Hiervoor ga je naar File -> Project Structure…. Vervolgens kies je Libraries en klik je op de knop met het plusteken (+). Kies voor Java en navigeer naar het gedownloade bestand graphlib.jar.

Opmerking: pas de graaf uit de input van de methode niet aan in je algoritme. Indien je dit wel doet, zullen de testen falen. Je mag eventueel wel een kopie van je invoergraaf maken.

Gebruik eventueel de testklasse SimpleTest⁵ om je oplossing lokaal te testen. Je kan hierin eenvoudig extra testgevallen toevoegen.