Hoe kan je exact 5 liter water afmeten uit een bron als je enkel beschikt over een kruik van 7 liter en een kruik van 3 liter? Dit soort vragen kom je vaak tegen in puzzelboeken. Meestal kunnen dergelijke problemen vrij eenvoudig opgelost worden op basis van intuïtie of via de methode van gissen-en-missen. In het boek Scripta Mathematica uit 1948 beschrijf H.D. Grossman echter een vernuftige methode om systematisch een oplossing te genereren.
Veronderstel dat beide kruiken een volume van $$a$$ en $$b$$ liter hebben en dat we $$c$$ liter willen afmeten. Voor het gegeven voorbeeld is $$a=7$$, $$b=3$$ en $$c=5$$. Er moet gelden dat $$a$$ en $$b$$ twee verschillende positieve gehele getallen zijn, dat $$a$$ en $$b$$ relatieve priemgetallen zijn (hun grootste gemene deler is gelijk aan 1) en dat één van beide kruiken groter is dan het gevraagde volume $$c$$. Anders is het probleem onoplosbaar, triviaal, of kan het gereduceerd worden tot kleinere getallen.

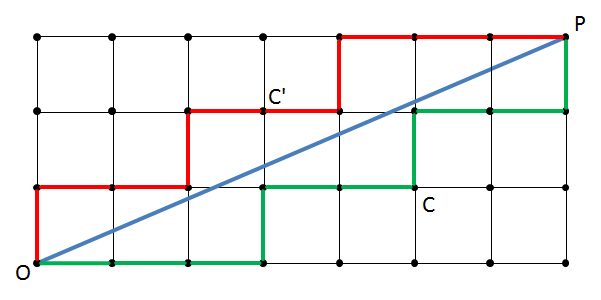
Beschouw een veld van roosterpunten (punten met gehele coördinaten) met daarin de lijn $$OP$$ (blauwe lijn) die $$O$$ in het punt $$(0, 0)$$ verbindt met $$P$$ in het punt $$(a, b)$$ (het punt $$(7, 3)$$ in ons voorbeeld). Teken nu een zigzaglijn $$Z$$ (groene lijn) die vanuit $$O$$ vertrekt, en steeds het huidige punt verbindt met zijn bovenbuur als deze niet boven de lijn $$OP$$ ligt, of anders het huidige punt verbindt met zijn rechterbuur. Er kan aangetoond worden dat $$Z$$ voor het eerst de lijn $$OP$$ snijdt in het punt $$P$$.
De zigzaglijn $$Z$$ vormt nu als het ware een beschrijving om de kruiken te vullen uit de bron, in elkaar over te gieten en leeg te maken, totdat op een bepaald punt één van beide kruiken exact de gevraagde hoeveelheid water bevat. Als we starten in $$O$$ en de zigzaglijn volgen, dan voeren we bij elke stap omhoog de volgende twee acties uit
Vul de $$a$$-liter kruik op met water uit de $$b$$-liter kruik.
Giet de $$a$$-liter kruik leeg. (niet nodig indien de $$b$$-liter kruik reeds $$c$$ liter water bevat)
en voeren we bij elke stap naar rechts de volgende twee acties uit
Giet de inhoud van de $$b$$-liter kruik in de $$a$$-liter kruik. (indien er water in de $$b$$-liter kruik zit)
Vul de $$b$$-liter kruik aan de bron. (niet nodig indien de $$a$$-liter kruik reeds $$c$$ liter water bevat)
We blijven $$Z$$ volgen totdat één van beide kruiken exact de gevraagde hoeveelheid water bevat. Er kan aangetoond worden dat er altijd zo een punt $$C$$ op de zigzaglijn te vinden is. Voor ons voorbeeld moeten dus de volgende acties uitgevoerd worden
Vul de 3-liter kruik aan de bron.
Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
Vul de 3-liter kruik aan de bron.
Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
Vul de 3-liter kruik aan de bron.
Vul de 7-liter kruik op met water uit de 3-liter kruik. (er kan nog 1 liter water overgegoten worden, zodat de 3-liter kruik nog 2 liter water bevat)
Giet de 7-liter kruik leeg.
Giet de inhoud van de 3-liter kruik in de 7-liter kruik. (de 7-liter kruik bevat nu 2 liter water)
Vul de 3-liter kruik aan de bron.
Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
De 7-liter kruik bevat nu 5 liter.
Er kan een alternatieve oplossing gevonden worden door een tweede zigzaglijn $$Z'$$ (rode lijn) te tekenen boven de lijn $$OP$$. Deze lijn gaat steeds naar de rechterbuur indien dat punt boven de lijn $$OP$$ ligt, anders naar de bovenbuur. De oplossing die we op deze manier aflezen kan gevonden worden door de rol van $$a$$ en $$b$$ om te wisselen in bovenstaande omschrijvingen. De alternatieve oplossing voor ons voorbeeld wordt dan
Vul de 7-liter kruik aan de bron.
Vul de 3-liter kruik op met water uit de 7-liter kruik.
Giet de 3-liter kruik leeg.
Vul de 3-liter kruik op met water uit de 7-liter kruik. (er zit nu nog 1 liter water in de 7-liter kruik)
Giet de 3-liter kruik leeg.
Giet de inhoud van de 7-liter kruik in de 3-liter kruik. (de 3-liter kruik bevat nu 1 liter water)
Vul de 7-liter kruik aan de bron.
Vul de 3-liter kruik op met water uit de 7-liter kruik. (er wordt dus 2 liter water overgegoten)
De 7-liter kruik bevat nu 5 liter.
Grossman zei hierover in zijn boek "There are always exactly two solutions which are in a sense complementary to each other."
Opgave
Schrijf een functie positie waaraan twee punten $$p_1$$ en $$p_2$$ moeten doorgegeven worden. Elk punt wordt voorgesteld door een tuple van twee natuurlijke getallen $$(x, y)$$. De functie moet een geheel getal teruggeven dat aangeeft of het punt $$p_2$$ op (waarde 0), boven (waarde 1) of onder (waarde -1) de rechte ligt die door de oorsprong $$(0, 0)$$ en het punt $$p_1$$ gaat.
Hint: Als $$p_1$$ het punt $$(a, b)$$ is, dan wordt de rechte die dit punt verbindt met de oorsprong beschreven door de vergelijking $$ay - bx = 0$$. Voor punten boven deze rechte is $$ay - bx$$ positief, en voor punten eronder is deze waarde negatief.Schrijf een functie broncode waaraan de natuurlijke getallen $$a$$, $$b$$ en $$c$$ moeten doorgegeven worden. De functie moet de acties uitschrijven die nodig zijn om exact $$c$$ liter water af te meten als je beschikt over een $$a$$-liter kruik en een $$b$$-liter kruik. Finaal moet ook uitgeschreven worden welke kruik de gevraagde hoeveelheid water bevat. Je mag er hierbij van uitgaan dat $$a$$ en $$b$$ verschillende positieve gehele getallen zijn, dat $$a$$ en $$b$$ relatieve priemgetallen zijn en dat één van beide kruiken groter is dan het gevraagde volume $$c$$. Zorg ervoor dat je implementatie dezelfde omschrijvingen van de acties gebruikt als in onderstaande voorbeeld staat aangegeven. De functie moet ook een optionele vierde parameter alternatief hebben, die aangeeft of de eerste oplossing (waarde False, de standaardwaarde) dan wel de alternatieve oplossing (waarde True) moet uitgeschreven worden.
Voorbeeld
>>> positie((3, 7), (3, 0))
-1
>>> positie((3, 7), (0, 3))
1
>>> positie((3, 7), (6, 14))
0
>>> broncode(7, 3, 5)
Vul de 3-liter kruik aan de bron.
Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
Vul de 3-liter kruik aan de bron.
Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
Vul de 3-liter kruik aan de bron.
Vul de 7-liter kruik op met water uit de 3-liter kruik.
Giet de 7-liter kruik leeg.
Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
Vul de 3-liter kruik aan de bron.
Giet de inhoud van de 3-liter kruik in de 7-liter kruik.
De 7-liter kruik bevat nu 5 liter.
>>> broncode(7, 3, 5, alternatief=True)
Vul de 7-liter kruik aan de bron.
Vul de 3-liter kruik op met water uit de 7-liter kruik.
Giet de 3-liter kruik leeg.
Vul de 3-liter kruik op met water uit de 7-liter kruik.
Giet de 3-liter kruik leeg.
Giet de inhoud van de 7-liter kruik in de 3-liter kruik.
Vul de 7-liter kruik aan de bron.
Vul de 3-liter kruik op met water uit de 7-liter kruik.
De 7-liter kruik bevat nu 5 liter.