Op 9 oktober 1817 werd de Universiteit Gent boven het doopvont gehouden in het Gentse stadhuis. Daarom stond het jaar 2017 volledig in het teken van de 200^e verjaardag van de UGent¹. Ter gelegenheid van deze festiviteiten hebben we speciaal voor de Universiteit Gent een priemgetal ontworpen.

Het priemgetal bestaat enkel uit de cijfers 1 en 8 — 9000 in totaal, verwijzend naar de postcode van de stad Gent — maar als je goed kijkt dan zie je dat het cijfer 2 ook één keer in het priemgetal voorkomt (aangeduid in het geel in bovenstaande figuur).

Opgave

In het tekstbestand hidden_words.txt² hebben we een lijst van woorden verstopt. Elke regel bevat een woord dat enkel bestaat uit letters (zowel hoofdletters als kleine letters zijn toegelaten), waarbij we voor, tussen en na de letters van het woord willekeurige cijfers hebben toegevoegd.

We gebruiken de notatie $$\mathcal{P}$$ voor de verzameling van alle woorden die enkel bestaat uit letters (zowel hoofdletters als kleine letters zijn toegelaten) waaraan extra cijfers kunnen toegevoegd worden voor, tussen en na de letters van het woord. Een zo lang mogelijke reeks opeenvolgende letters in $$p \in \mathcal{P}$$ noemen we een groep. Gevraagd wordt:

1. Bepaal zo kort mogelijke reguliere expressies voor de volgende deelverzamelingen van $$\mathcal{P}$$:

   • $$\mathcal{P}_1 = \{\,p \in \mathcal{P}\,|\,$$ er staan geen cijfers tussen de letters van het woord in $$p\,\}$$

     voorbeelden:	39568250269955376311912572precondition005426787530581443236416842014020466976603 $$\in \mathcal{P}_1$$
     	18958535313605793170095290529923mathematici2779805995331496368099837070an1084015 $$\not\in \mathcal{P}_1$$

   • $$\mathcal{P}_2 = \{\,p \in \mathcal{P}\,|\, p$$ bevat een reeks van minstens drie opeenvolgende oneven cijfers zonder letters ertussen$$\,\}$$

     voorbeelden:	28411868663721472744440442174386579246325770883aldo29349020307976l83871941955671 $$\in \mathcal{P}_2$$
     	24054592017722795066151886136772461985802800654731523434656051391micr9otechnique $$\not\in \mathcal{P}_2$$

     Opmerking

     Met opeenvolgende oneven cijfers bedoelen we de reeks 1, 3, 5, 7 en 9.

   • $$\mathcal{P}_3 = \{\,p \in \mathcal{P}\,|\, p$$ bevat minstens vijf groepen$$\,\}$$

     voorbeelden:	30474967583414287634529432102615285637683he6244139301523560terotr4565918op1hi15c $$\in \mathcal{P}_3$$
     	683929629607366384846442641925771941514gues230109sworks7958462277260966903049357 $$\not\in \mathcal{P}_3$$

   • $$\mathcal{P}_4 = \{\,p \in \mathcal{P}\,|\,$$eerste en laatste letter van $$p$$ worden resp. voorafgegaan en gevolgd door zelfde cijfer$$\,\}$$

     voorbeelden:	9366947533557157204181560054978886808334627588608299ang0io752901403085mat93a9535 $$\in \mathcal{P}_4$$
     	39384286489764957586401269744226275965emissivi64159406666255631009ty911316262761 $$\not\in \mathcal{P}_4$$

   Geef telkens een Unix commando waarin de reguliere expressie gebruikt wordt door een commando uit de grep familie om enkel de regels van het tekstbestand naar stdout te schrijven waarvan het patroon $$p$$ behoort tot $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$.

   Opmerking

   Gebruik voor deze opgave een recente versie van GNU grep. Op helios is een recente versie van GNU grep geïnstalleerd, maar Mac OS X gebruikt standaard typisch een oudere versie van GNU grep. Mac gebruikers kunnen voor de zekerheid dus best hun grep versie updaten naar de meest recente versie.

2. Beschouw de verzamelingen $$\mathcal{P}_1$$, $$\mathcal{P}_2$$, $$\mathcal{P}_3$$ en $$\mathcal{P}_4$$ zoals hierboven gedefinieerd. Gebruik nu deze verzamelingen om op de volgende manier een boodschap bestaande uit vier woorden te achterhalen:

   • het eerste woord staat op de unieke regel uit de verzameling $$\mathcal{P}_1 \cap \mathcal{P}_2$$

   • het tweede woord staat op de unieke regel uit de verzameling $$\mathcal{P}_2 \cap \mathcal{P}_3$$

   • het derde woord staat op de unieke regel uit de verzameling $$\mathcal{P}_3 \cap \mathcal{P}_4$$

   • het vierde woord staat op de unieke regel uit de verzameling $$\mathcal{P}_4 \cap \mathcal{P}_1$$

   Geef telkens een Unix commando dat elk van deze woorden opzoekt in het bestand en uitschrijft naar stdout, zonder evenwel het woord letterlijk uit te schrijven (bv. echo xxx). Hierbij moet het woord uitgeschreven worden zonder de cijfers die voor, tussen na de letters van het woord staan.

Epiloog

Het ontwerp van het priemgetal van de Universiteit Gent is geïnspireerd op deze video die gemaakt werd door Numberphile³.

De video toont een verrassende afbeelding die te vinden is in een klein kadertje dat aan de muur hangt in de Senior Combination Room in Trininty College⁴, een college dat behoort bij de Universiteit van Cambridge. De jonge onderzoeker James McKee bedacht een priemgetal van 1350 cijfers dat een sterke gelijkenis vertoont met het wapenschild van de Universiteit van Cambridge. Ook het aantal cijfers is niet toevallig gekozen, want het verwijst naar het jaar waarin bisschop William Bateman⁵ de universiteit gesticht heeft.

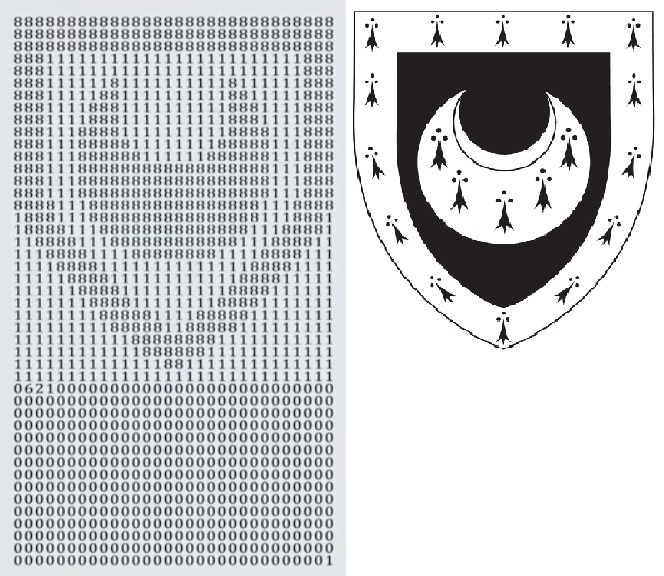
Nu blijkt het vinden van een priemgetal dat een bepaalde afbeelding weergeeft, eenvoudiger te zijn dan je op het eerste gezicht misschien zou denken. In de beschrijving onder de video legt McKee uit hoe hij tot het ontwerp van het priemgetal gekomen is:

De meeste cijfers van het priemgetal $$p$$ werden vastgelegd zodat i) tweede derde van de cijfers bovenaan het gewenste patroon vormen en ii) één derde van de cijfers onderaan ervoor zorgen dat $$p - 1$$ een mooi grote (samengestelde) priemfactor $$F$$ heeft, waarbij de ontbinding in priemgetallen van $$F$$ gekend is. Voor getallen van deze vorm bestaat een eenvoudige en snelle manier om te controleren of het priemgetallen zijn. Tenslotte werd een klein aantal cijfers (je kan makkelijk zien welke) gebruikt om systematisch op te tellen vanaf 1, totdat een getal $$p$$ gevonden werd dat een priemgetal is.

Het inspireerde ook wiskundestudent Jack Hodkinson van de Universiteit van Cambridge om een priemgetal te ontwerpen met de afbeelding⁶ van Corpus Christi College⁷, waarin hij zijn eigen initialen en geboortedatum wist te verwerken.

Om het priemgetal van de Universiteit Gent te ontwerpen, zijn we vertrokken van het logo dat gebruikt werd voor de 200^e verjaardag van de UGent.

Dit logo hebben we omgezet naar een ASCII afbeelding bestaande uit 9000 cijfers (als verwijzing naar de postcode van de stad Gent⁸), verdeeld over 75 rijen van elk 120 enen en achten. Voor de weergave van het priemgetal kozen we het lettertype Bimini, omdat het een mooi contrast gaf tussen "zware" achten (die de blauwe pixels voorstellen) en "lichte" enen (die de witte pixels voorstellen). Gelukkig was de pixel rechtsonder wit, omdat het priemgetal dat we voor ogen hadden onmogelijk even kon zijn.

Daarna schreven we een Python programma dat dit initiële getal — dat nog geen priemgetal was, maar wel het gewenste patroon weergaf — moest omvormen tot een priemgetal. Hiervoor overliep het programma systematisch alle cijfers 8 in het initiële getal, verving die telkens door één van de andere cijfers (niet 1 of 8) en controleerde of het getal dat zo bekomen werd een priemgetal was. Om snel te controleren of een getal van 9000 cijfers een priemgetal is, maakten we gebruik van de Miller-Rabin-priemgetaltest⁹. Dit algoritme heeft het altijd bij het rechte eind als het zegt dat een getal geen priemgetal is, maar het kan enkel met (zeer) grote zekerheid stellen dat een getal wel een priemgetal is. Om finaal te controleren dat een kandidaat-priemgetal wel degelijk priem was, hebben we gebruikgemaakt van de fantastische app van Dario Alpern¹⁰ om onszelf absolute zekerheid te geven.

Hoe wisten we nu zo zeker dat dit zou werken? Wel, de priemgetalstelling¹¹ zegt ons dat er ongeveer $$\frac{n}{\log{n}}$$ priemgetallen zijn die kleiner zijn dan $$n$$. Er zijn met andere woorden ongeveer \[ \frac{10^{9000}}{\log{10^{9000}}} - \frac{10^{8999}}{\log{10^{8999}}} \approx   4.34 \times 10^{8995} \] priemgetallen met 9000 cijfers. Dat betekent dat bij benadering één op de 21.000 getallen met 9000 cijfers een priemgetal zou moeten zijn. Deze schatting hebben we uiteraard niet met de hand op de achterkant van een bierkaartje berekend, want ook hier schoot Python ons ter hulp (de module Decimal zorgt ervoor dat we met grote floating point getallen kunnen rekenen zonder afrondingsfouten).

>>> from decimal import Decimal
>>> n = Decimal(10 ** 9000)
>>> m = Decimal(10 ** 8999)
>>> schatting = lambda x : x / x.ln()
>>> aantal_priemgetallen_met_9000_cijfers = schatting(n) - schatting(m)
>>> aantal_priemgetallen_met_9000_cijfers
Decimal('4.342891196471751863968210190E+8995')
>>> aantal_getallen_met_9000_cijfers = 9 * m
>>> aantal_getallen_met_9000_cijfers / aantal_priemgetallen_met_9000_cijfers
Decimal('20723.52171132395093158056936')

De even getallen mochten we bij voorbaat al buiten beschouwing laten, dus dat reduceert onze zoekruimte al met de helft. Ook de cijfers 0, 3, 6 en 9 hoefden we niet te controleren als vervanging van één van de achten, omdat deze in combinatie met 7660 enen en 1339 achten altijd een drievoud opleveren. Enkel de cijfers 2, 4, 5 en 7 bleven dus nog over als mogelijke vervanging voor één van de achten.

Het zoeken naar ons priemgetal zou dus zeker niet zo tijdrovend zijn als het zoeken van de spreekwoordelijke speld in een hooiberg. Maar als je je bedenkt dat het ons een paar minuten kost om te achterhalen of een getal van 9000 cijfers een priemgetal is, was de voorspelling dat we toch een dikke maand zoet zouden zijn vooraleer we ons priemgetal zouden vinden. Gelukkig was er ook nog de supercomputer van de UGent¹² (met dank aan de samenwerking met het Vlaams Supercomputer Centrum¹³), waardoor we heel wat getallen tegelijkertijd konden controleren. Uiteindelijk leverde het 2942^e getal dat we controleerden al een priemgetal op, waardoor onze rudimentaire voorspelling van hierboven zelfs een overschatting bleek te zijn.