Associaties tussen twee variabelen
Tot nog toe zijn we hoofdzakelijk ingegaan op zogenaamde univariate beschrijvingen waarbij slechts 1 variabele onderzocht wordt. In de meeste wetenschappelijke studies wenst men echter associaties tussen 2 of meerdere variabelen te onderzoeken, bijvoorbeeld tussen een interventie en de daarop volgende respons. In deze Sectie onderzoeken we hoe associaties tussen 2 variabelen kunnen beschreven worden. We maken daarbij onderscheid naargelang het type van de variabelen.
Associatie tussen twee kwalitatieve variabelen
Als twee kwalitatieve variabelen niet veel verschillende waarden aannemen, dan is een kruistabel aangewezen om hun associatie voor te stellen. In deze tabel worden de verschillende waarden die de ene variabele aanneemt in de kolommen uitgezet en de verschillende waarden die de andere variabele aanneemt in de rijen. In elke cel van de tabel (die overeenkomt met 1 specifieke combinatie van waarden voor beide variabelen) wordt de frequentie neergeschreven.
| 12.0\_18.5 | 18.5\_to\_24.9 | 25.0\_to\_29.9 | 30.0\_plus | |
|---|---|---|---|---|
| female | 629 | 1616 | 1179 | 1402 |
| male | 648 | 1295 | 1485 | 1349 |
Tabel 10 toont zo’n kruistabel voor het aantal mannen en vrouwen per BMI klasse. Dergelijke eenvoudige kruistabel met slechts 2 rijen en 4 kolommen, noemt men ook een \(2\times 4\) tabel.
Associatie tussen één kwalitatieve en één continue variabele
Boxplots zijn meer compact dan een histogram en laat om die reden gemakkelijker vergelijkingen tussen verschillende groepen toe. Twee dergelijke boxplots worden getoond in Figuur 8.
NHANES %>%
ggplot(aes(x = Gender,y = log(DirectChol))) +
geom_boxplot() +
ylab("log(Direct Cholestorol)")
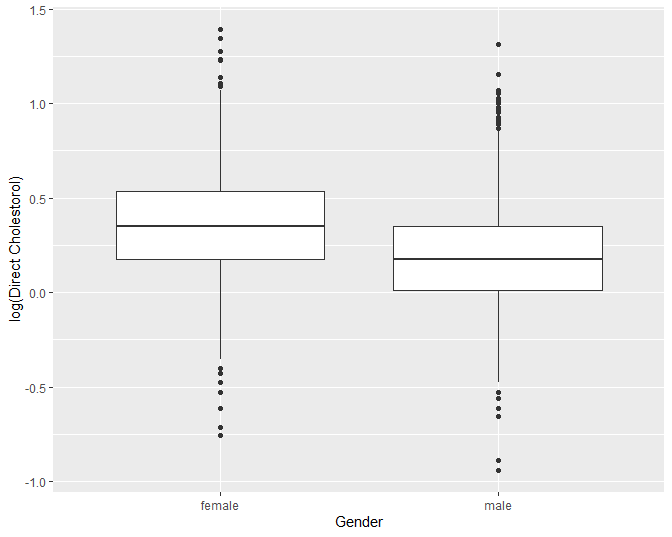
Figuur 8: Boxplot van log-getransformeerde directe HDL cholestorol concentratie in functie van Gender voor alle subjecten van de NHANES studie.
Op basis van deze figuur stellen we vast dat hogere log-cholestorol concentraties geobserveerd worden bij vrouwen dan bij mannen, maar dat de variabiliteit van de log-concentraties vergelijkbaar is tussen de 2 groepen. De vraag blijft of we hier kunnen spreken van een systematisch hogere log-cholestorol concentratie tussen vrouwen en mannen. We zullen in Hoofdstuk 5 dieper op deze vraag ingaan.
Figuur 8 kan men samenvatten door gemiddelde verschillen tussen beide groepen te rapporteren. Hier stellen we een gemiddeld verschil van 0.17 in directe HDL cholestorol concentratie vast op de log schaal tussen vrouwen en mannen. Gezien we weten dat \(\log(C_2)-\log(C_1)=\log(C_2/C_1)\) weten we dat de HDL cholestorol concentratie in de NHANES studie gemiddeld 1.19 keer hoger ligt voor vrouwen dan voor mannen.
In de introductie hebben we bij het microbiome voorbeeld gezien dat het ook erg nuttig is om de ruwe data weer te geven op de boxplot. Als het aantal gegevens niet te hoog is kunnen we eenvoudig een extra laag toevoegen met de originele datapunten. Merk op dat het wel belangrijk is om de outliers dan niet weer te geven in de boxplot, anders zal men deze twee keer afbeelden. Eens in de geom_boxplot laag een eens in de geom_point laag. Daarom zetten we het symbool voor de outliers op NA.
In onderstaande grafiek plotten we de relatieve abundanties van Staphylococcus van de oksel microbiome case study.
- We pipen het
apdataframe naarggplot - We selecteren de data voor de plot via
ggplot(aes(x=trt,y=rel)) - We voegen laag toe voor de boxplot dmv de functie
geom_boxplot(). Merk op dat we het argumentoutlier.shapeop NA (not available) zettenoutlier.shape=NAin thegeom_boxplotfunctie omdat we anders outliers twee keer weer zullen geven. Eerst via de boxplot laag en daarna omdat we een laag met alle ruwe data toevoegen aan de plot. - We geven de ruwe data weer via de
geom_point(position="jitter")functie. We gebruiken hierbij het argument position=‘jitter’ zodat we wat random ruis toevoegen aan de x-cordinaat zodat de gegevens elkaar niet overlappen.
ap <- read_csv("https://raw.githubusercontent.com/GTPB/PSLS20/master/data/armpit.csv")
ap %>%
ggplot(aes(x=trt,y=rel)) +
geom_boxplot(outlier.shape=NA) +
geom_point(position="jitter")
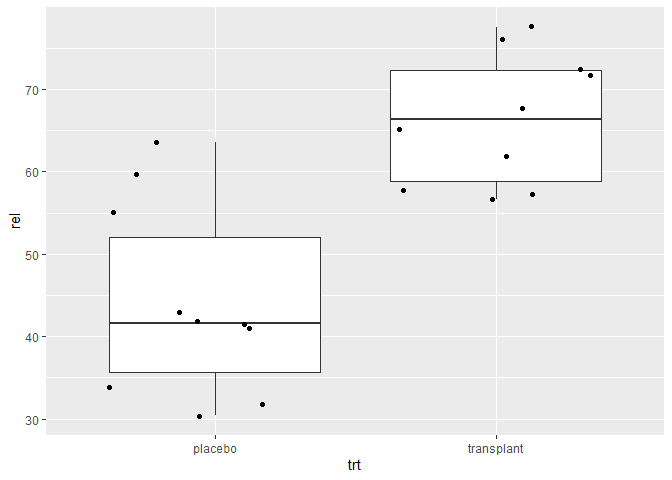
Dot-plots zijn bijzonder interessant in pre-test post-test designs waar dezelfde subjecten op verschillende tijdstippen worden geobserveerd. In dat geval kunnen de uitkomsten uitgezet worden op de Y-as en de tijdstippen op de X-as, en kunnen de metingen voor eenzelfde subject worden verbonden met een lijn.
Een voorbeeld hiervan is weergegeven in Figuur 9. De figuur vat de gegevens samen van de captopril studie die de centrale dataset vormt van Hoofdstuk 5. In de studie wenst men het effect van een bloeddrukverlagend geneesmiddel captopril evalueren. Voor elke patiënt in de studie werd de systolische bloeddruk twee keer gemeten: één keer voor en één keer na de behandeling met het bloeddruk verlagende medicijn captopril. In Figuur 9 worden de metingen van dezelfde patiënt met een lijntje verbonden. Hierdoor krijgen we een heel duidelijk beeld van de gegevens. Namelijk, we krijgen een sterke indruk dat de bloeddruk daalt na het toedienen van captopril gezien we bijna voor alle patiënten een daling observeren.
#Eerst lezen we de data in.
#Deze bevindt zich in de subdirectory dataset
#Het is een tekstbestand waarbij de kolommen van elkaar gescheiden zijn d.m.v comma's.
#sep=","
#De eerste rij bevat de namen van de variabelen
captopril <- read.table("https://raw.githubusercontent.com/statOmics/sbc20/master/data/captopril.txt",header=TRUE,sep=",")
head(captopril)
## id SBPb DBPb SBPa DBPa
## 1 1 210 130 201 125
## 2 2 169 122 165 121
## 3 3 187 124 166 121
## 4 4 160 104 157 106
## 5 5 167 112 147 101
## 6 6 176 101 145 85
captoprilTidy <-
captopril %>%
gather(type,bp,-id)
captoprilTidy %>%
filter(type%in%c("SBPa","SBPb")) %>%
mutate(type = factor(
type,
levels = c("SBPb","SBPa"))
) %>%
ggplot(aes(x=type,y=bp)) +
geom_line(aes(group = id)) +
geom_point()
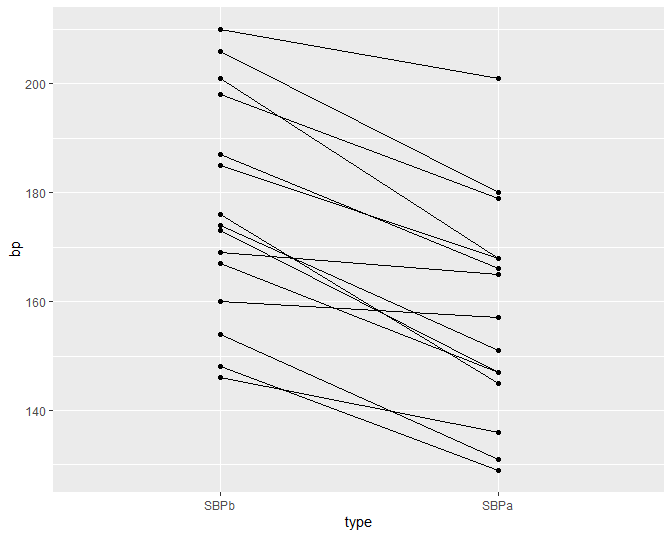
Figuur 9: Dotplot van de systolische bloeddruk in de captopril studie voor en na het toedienen van het bloeddruk verlagend middel captopril.