Practicum 2 case

In this practicum we will simulate a statistical problem in R. This approach is based on the law of large numbers, a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and will tend to become closer to the expected value as more trials are performed. This is especially usefull for problems that are hard to solve mathematically, or to give you a quick estimate of the expected value.

Let’s demonstrate the approach with a coin flip example: If you keep flipping a fair coin the frequency of heads will tend to become 0,5. In the graph below we simulated the coin flip experiment for you:

Heads frequency

Heads frequency in function of number of coin tosses

We will simulate the chance that a random group of 5 people has an avarage IQ above 110. This question is heavily related to the central limit theorem, a theorem you have not yet learned that will allow you to calculate the exact value of this chance. This exercise is a perfect example to show of the power of computing power in statistics.

The intelligence quotient (IQ) is a total score derived from a set of standardized tests or subtests designed to assess human intelligence. The IQ is a well known psychological statistic but it also has statistical relevance. The IQ scores are scaled to match the Bell schaped normal distribution with an average of 100 and a standard deviation of 15.

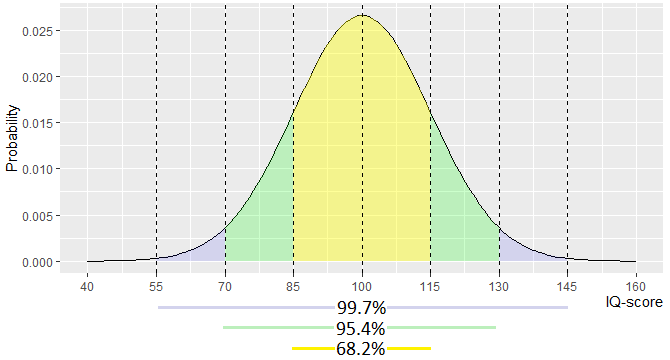
IQ density curve

density curve of IQ scores

Exercise

Let’s start by defining a function to generate a number of iq values and return the mean.

Define a function group_iq that takes one argument n and returns the mean of n random people’s iq. You can do this by sampling n random iq values from a normal distribution with mean 100 and standard deviation 15 using the rnorm() function and compute the mean.

Generating random data

R has build in functions to generate data from some basic distributions, to generate normally distributed (IQ) data you can use the rnorm function. Check the help page (help(rnorm)) for more information about using this function.