Data Exploratie & Beschrijvende Statistiek
Eens de data zijn geobserveerd, is het belangrijk om deze te exploreren
om inzicht te krijgen in hun verdeling en karakteristieken. Vervolgens
zullen we de gegevens samenvatten zodat we het effect van interesse
kunnen kwantificeren in de steekproef. In deze studie is de systolische
bloeddruk en de diasystolische bloeddruk gemeten voor elke patiënt voor
en na het toedienen van captopril. De data is beschikbaar in een
tekstbestand met naam captopril.txt op de github pagina
https://raw.githubusercontent.com/statOmics/sbc20/master/data/captopril.txt.
We zullen eerst exploreren welke figuren nuttig zijn in onze context. In
wetenschappelijke artikels worden vaak figuren gemaakt van het
gemiddelde en de standaardafwijking (zie Figuur
14).
#Eerst lezen we de data in.
#Deze bevindt zich in de subdirectory dataset
#Het is een tekstbestand waarbij de kolommen van elkaar gescheiden zijn d.m.v kommas.
#sep=","
#De eerste rij bevat de namen van de variabelen
captopril <- read.table("https://raw.githubusercontent.com/statOmics/sbc20/master/data/captopril.txt",header=TRUE,sep=",")
head(captopril)
## id SBPb DBPb SBPa DBPa
## 1 1 210 130 201 125
## 2 2 169 122 165 121
## 3 3 187 124 166 121
## 4 4 160 104 157 106
## 5 5 167 112 147 101
## 6 6 176 101 145 85
captoprilTidy <- captopril %>% gather(type,bp,-id)
captoprilTidy %>%
group_by(type) %>%
summarize_at("bp",list(mean=~mean(.,na.rm=TRUE),
sd=~sd(.,na.rm=TRUE),
n=function(x) x%>%is.na%>%`!`%>%sum)) %>%
mutate(se=sd/sqrt(n))
## # A tibble: 4 x 5
## type mean sd n se
## <chr> <dbl> <dbl> <int> <dbl>
## 1 DBPa 103. 12.6 15 3.24
## 2 DBPb 112. 10.5 15 2.70
## 3 SBPa 158 20.0 15 5.16
## 4 SBPb 177. 20.6 15 5.31
captoprilTidy %>%
group_by(type) %>%
summarize_at("bp",list(mean=~mean(.,na.rm=TRUE),
sd=~sd(.,na.rm=TRUE),
n=function(x) x%>%is.na%>%`!`%>%sum)) %>%
mutate(se=sd/sqrt(n)) %>%
ggplot(aes(x=type,y=mean)) +
geom_bar(stat="identity") +
geom_errorbar(aes(ymin=mean-se, ymax=mean+se),width=.2) +
ylim(0,210) +
ylab("blood pressure (mmHg)")
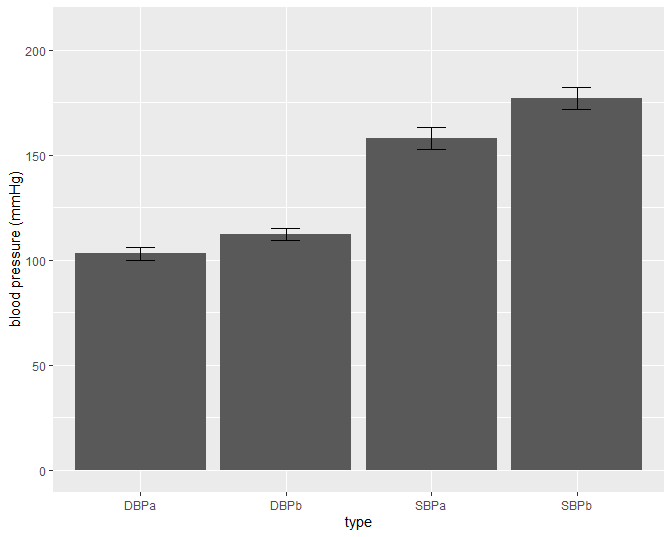
Figuur 14: Barplot van de gemiddelde bloeddruk in de captopril studie. De foutenvlag is 2x de standaard deviatie op de metingen (SBPb: systolic BloodPressure before, DBPb: Diasystolic BloodPressure before, SBPa: systolic BloodPressure after, DBPa: Diasystolic BloodPressure after).
De figuur is echter niet informatief. De hoogte van de balken zegt enkel iets over het gemiddelde. We kunnen onmogelijk weten wat het bereik van de ruwe gegevens is bijvoorbeeld. Daarom is het beter om de gegevens zo ruw mogelijk weer te geven in een plot. We kunnen hiervoor bijvoorbeeld gebruik maken van boxplots (Figuur 15). Aangezien we maar over 15 patiënten beschikken kunnen we ook de ruwe datapunten toevoegen. In de figuur zien we dat de systolische bloeddruk in de steekproef gemiddeld lager ligt na de behandeling met captopril. We krijgen ook een duidelijk beeld op het bereik van de data.
#toevoegen van originele datapunten op de plot
#jitter zal de punten random verspreiden
captoprilTidy %>%
ggplot(aes(x=type,y=bp)) +
geom_boxplot(outlier.shape=NA) +
geom_point(position="jitter") +
ylim(0,210)
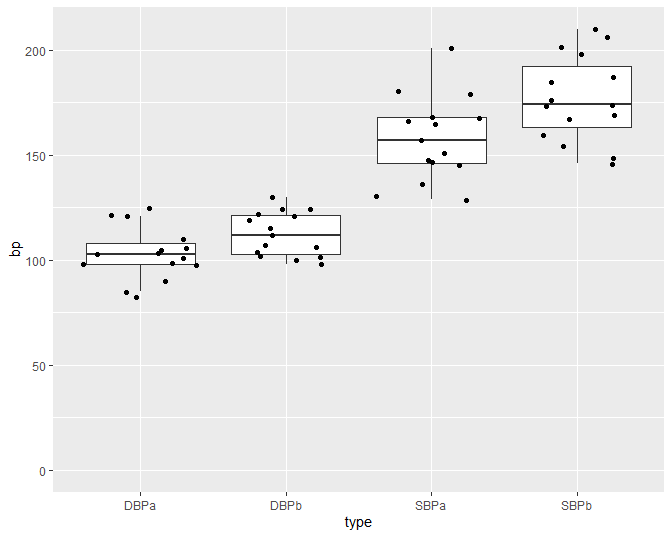
Figuur 15: Boxplot en ruwe data van de bloeddruk in de captopril studie (SBPb: systolic BloodPressure before, DBPb: Diasystolic BloodPressure before, SBPa: systolic BloodPressure after, DBPa: Diasystolic BloodPressure after).
Als alle bloeddrukmetingen onafhankelijk zouden zijn dan is Figuur 15 een goede figuur om de data te exploreren. We weten echter dat de metingen voor en na het toedienen van captopril afkomstig zijn van dezelfde patiënt. We kunnen die informatie toevoegen in een dotplot zoals we illustreren voor de systolische bloeddruk in Figuur 16. In deze figuur zijn de twee bloeddrukmetingen voor dezelfde persoon verbonden met een lijn. Deze figuur geeft duidelijk weer dat de bloeddruk daalt voor elke patiënt wat een sterke aanwijzing is dat er een effect is van het toedienen van captopril op de systolische bloeddruk.
#De geom_line layer laat ons de bloeddrukmetingen voor dezelfde personen verbinden met een lijn
captoprilTidy %>%
filter(type%in%c("SBPa","SBPb")) %>%
mutate(type=factor(type,levels=c("SBPb","SBPa"))) %>%
ggplot(aes(x=type,y=bp)) +
geom_line(aes(group = id)) +
geom_point()
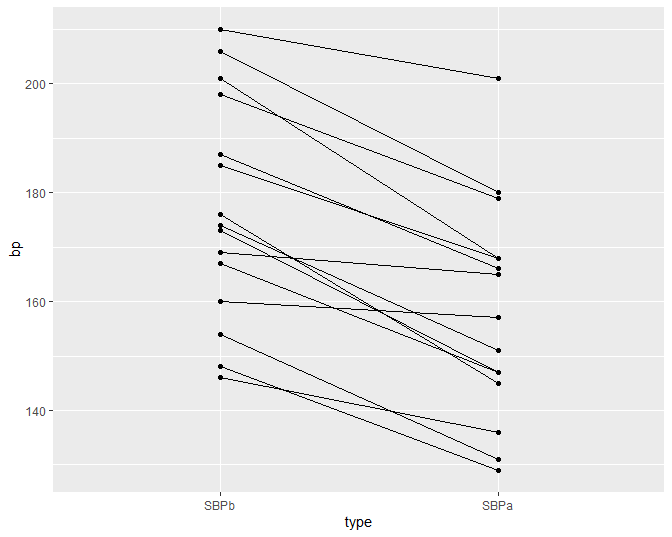
Figuur 16: Dotplot van de systolische bloeddruk in de captopril studie voor en na het toedienen van captopril.
Aangezien we slechts twee bloeddrukmetingen hebben per patiënt kunnen we het effect van captopril ook berekenen per patiënt door het verschil in de systolische bloeddruk na en voor de toediening van captopril te berekenen. Dat is één van de voordelen van een pre-test/post-test design.
#we selecteren de bloeddruk na en voor toedienen
#uit de dataset via naam van variabele d.m.v. $-teken
#en berekenen het verschil
delta <- captopril$SBPa-captopril$SBPb
captopril$deltaSBP <- delta
captopril %>%
ggplot(aes(x="Systolic blood pressure",y=deltaSBP)) +
geom_boxplot(outlier.shape=NA) +
geom_point(position="jitter")+
ylab("Difference (mm mercury)") +
xlab("")
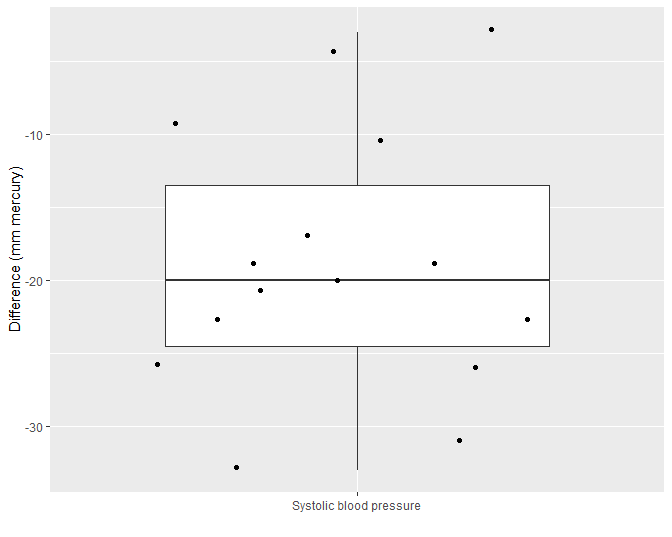
Figuur 17: Boxplot van het verschil in systolische bloeddruk voor en na het toedienen van captopril.
We observeren in Figuur 17 een bloeddrukdaling voor elke patiënt in de steekproef wat opnieuw een heel sterke indicatie is voor een gunstig effect van het toedienen van captopril op de bloeddruk. De verschillen in systolische bloeddruk zijn een goede maat om het effect van captopril te bepalen. We kunnen de data als volgt samenvatten.
captopril %>%
summarize_at("deltaSBP",list(mean=~mean(.,na.rm=TRUE),
sd=~sd(.,na.rm=TRUE),
n=function(x) x%>%is.na%>%`!`%>%sum)) %>%
mutate(se=sd/sqrt(n))
## mean sd n se
## 1 -18.93333 9.027471 15 2.330883
We observeren gemiddeld een systolische bloeddrukdaling van 18.93 mmHg en een standaard deviatie van 9.03 mmHg.
Schatten
Pre-test/post-test design: Het effect van captopril in de steekproef kan worden bestudeerd door het verschil te bepalen in systolische bloeddruk na en voor de behandeling (\(X=\Delta_\text{na-voor}\))! Hoe kunnen we de bloeddrukverschillen modelleren en het effect van het toedienen van captopril schatten?
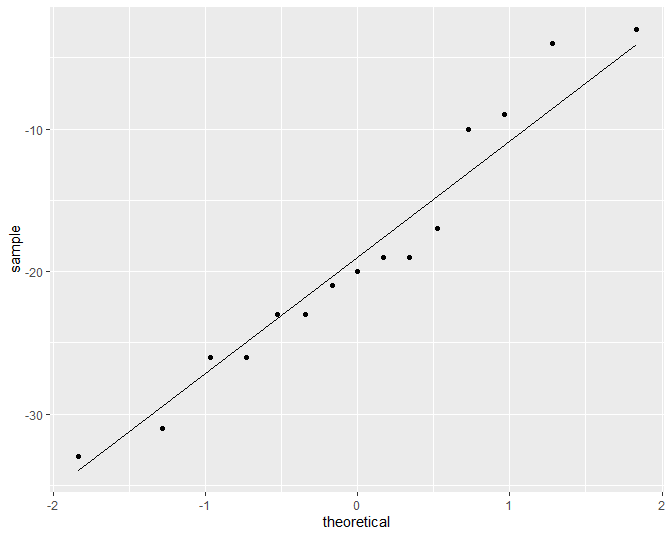
Figuur 18: QQ-plot voor het verschil in systolische bloeddruk voor en na het toedienen van captopril.
We zien geen grote afwijkingen van Normaliteit in Figuur 18. We kunnen de bloeddrukverschillen dus modelleren aan de hand van een Normale verdeling en kunnen het effect van captopril in de populatie beschrijven a.d.h.v. de gemiddelde bloeddrukverschil \(\mu\). Het bloeddrukverschil \(\mu\) in de populatie kan worden geschat a.d.h.v. het steekproefgemiddelde \(\bar x\)=-18.93 en de standaard afwijking \(\sigma\) a.d.h.v. de steekproefstandaarddeviatie \(\text{SD}\)=9.03.
We vragen ons nu af of het effect dat we observeren in de steekproef groot genoeg is om te kunnen spreken van een effect van captopril in de populatie. We weten immers dat onze statistiek voor de schatting van het effect van captopril in de populatie berekend wordt op basis van de gegevens uit de steekproef en daarom zal variëren van steekproef tot steekproef. Het is daarom belangrijk om een inzicht te krijgen in hoe het steekproefgemiddelde zal variëren van steekproef tot steekproef.