De berekening van \(\pi\) in de opgave Benadering voor pi aangepast¹ geeft geen enkele garantie dat de 10 decimalen die je uitschrijft ook correct zijn. In deze oefening proberen we dit probleem op te lossen.

Problemen met reële getallen

Op One million digits of pi² kan je een heel goede benadering vinden voor \(\pi\). Download het programma pi.py³. In de code werd deze benadering in een string geplakt (beperkt tot 65 digits). Voer dit programma uit en merk op:

De numerieke waarde van \(\pi\) is niet echt wat je verwacht.
Enkel de eerste 15 decimalen (3.141592653589793) zijn correct. Dit zal later verklaard worden (in basiskennis).
De waarde van \(\pi\) kan dus in Python maar tot 15 decimalen worden benaderd.
Ook de constante math.pi bevat exact deze benadering, en is dus maar correct tot 15 decimalen.

Opdracht

Schrijf een programma dat een positief geheel getal \(k\) inleest. Dit getal bepaalt hoeveel cijfers na de komma correct moeten zijn. Pas de berekening aan zodat de waarde van \(\pi\) correct is tot \(k\) cijfers na de komma. Uiteraard kan je dit enkel zinvol testen met \(k<15\). Het programma schrijft de waarde van \(\pi\) dan ook uit met \(k\) decimalen.

Je gebruikt de aangepaste formule:

\[\pi = 3 + \frac{4}{2*3*4} - \frac{4}{4*5*6} + \frac{4}{6*7*8} - \frac{4}{8*9*10} + ...\]

Je moet het hoofdprogramma toevoegen in de gegeven procedure main().

Tips

Je mag geen gebruik maken van de ‘exacte’ waarde voor \(\pi\) uit de module math of hardgecodeerd. Dit wordt apart gecontroleerd in Dodona!
Het is ook fout om een speciaal geval apart te beschrijven met if, om door de testen te geraken. Dit wordt ook gecontroleerd!
In deze oefening kan je niet op voorhand bepalen hoeveel termen je moet berekenen. Vervang de for - lus door een while - lus.
Het aantal cijfers dat correct moet zijn na de komma bepaalt de nauwkeurigheid van de berekening. Je wilt zeker zijn dat het \(k\)-de digit juist is, dus laat je een maximale fout toe van \(10^{-k-1}\) met \(k\) het gewenste aantal cijfers na de komma.
Merk op dat de termen afwisselend positief en negatief zijn. De reeks is convergent (naar \(\pi\)), door het kenmerk van Leibniz⁴. In de grafiek hieronder zie je de eerste vijf partiële sommen.

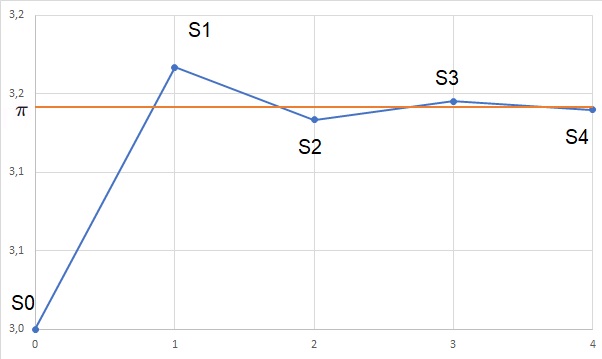
Reeksom

Op de grafiek kan je zien dat het gemiddelde van twee opeenvolgende partiële sommen (bijvoorbeeld \(\frac{S_3+S_4}{2}\)) een goede benadering is voor \(\pi\).

Gebruik als benadering voor \(\pi\) het gemiddelde van twee opeenvolgende partiële sommen. Als het verschil tussen twee opeenvolgende benaderingen kleiner is dan \(10^{-k-1}\) kan je de berekening stoppen.
Gebruik round om het resultaat af te printen met \(k\) decimalen.

Invoer

Het gewenste aantal decimalen (\(k\)).

Uitvoer

De berekende waarde voor \(\pi\) met exact \(k\) decimalen.

Voorbeeld1

Het aantal gewenste decimalen is 6

>>> main()
3.141593

Voorbeeld2

Het aantal gewenste decimalen is 14

>>> main()
3.1415926535898

Merk op dat het veertiende decimaal hier 0 is. Python toont voor getallen geen nullen achteraan, dus zie je maar 13 decimalen.

Als enkel deze testset faalt, dan moet je de tips nog eens goed lezen!