In het handelsreizigersprobleem (Traveling Salesman Problem, TSP) wordt gezocht naar een rondreis of Hamiltoniaanse cykel van minimaal gewicht in een complete gewogen graaf G. Een speciaal geval is he Euclidische handelsreizgersprobleem, waarbij de (niet-negatieve) boogkosten voldoen aan de driehoeksongelijkheid, m.a.w. wanneer de toppen corresponderen met punten in het vlak en de boogkosten corresponderen met de Euclidische afstand tussen twee punten.

TSP is een onhandelbaar probleem, hetgeen in de praktijk betekent dat er geen efficient alogritme (m.a.w. met polynomiale tijd) bestaat voor het bepalen van de optimale rondreis. In de praktijk worden dan ook algoritmen gebruikt die een korte rondreis bepalen, m.a.w. een benadering van de optimale rondreis.

Een eenvoudig gretig algoritme start in een willekeurige top v, start een pad dat de goedkoopste boog uit v bevat, en dan herhaaldelijk dit pad uitbreidt door telkens de goedkoopste boog van het eindpunt van het pad naar een onbezochte top, totdat alle toppen bezocht zijn. Uiteindelijk wordt het pad gesloten door de boog van de laatste top op het pad naar de starttop v toe te voegen.

Opgave

Schrijf een Python functie greedyTSP die een bestandsnaam als parameter krijgt. Het bestand bevat de coordinaten van een verzameling punten in het vlak, elke lijn heeft de x- en y-coordinaat van een punt. Voor deze verzameling van punten wordt de afstandsmatrix opgebouwd, die voor elk paar punten de Euclidische afstand bevat. Dit stelt een complete gewogen graaf voor met toppen i, genummerd van 0 tot n-1 (waarbij n het aantal punten is), en met booggewichten w(i,j) de afstand tussen punten p_i and p_j. De functie voert het bovenstaande gretige algoritme uit, startend in top 0, voor het bekomen van een korte rondreis. De rondreis wordt teruggegeven als een lijst van toppen.

Voorbeeld

In het onderstaande voorbeeld wordt verondersteld dat het bestand data15_2.txt¹ zich in de huidige directory bevindt.

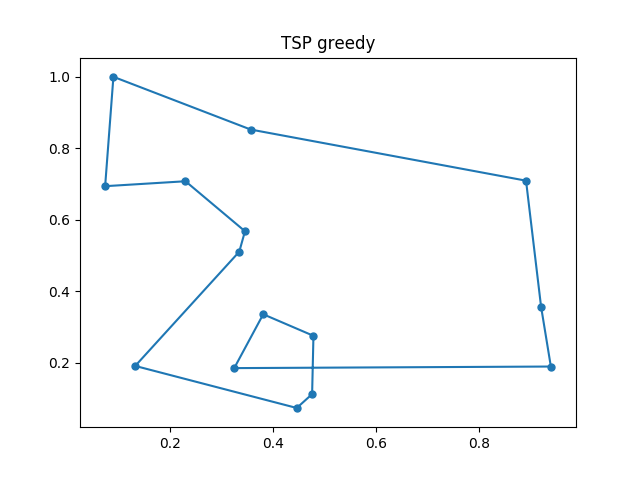
>>> greedyTSP("data15_2.txt")
[0, 3, 6, 10, 2, 7, 5, 9, 12, 14, 8, 13, 1, 11, 4, 0]