Het getal \(\pi\) kan op de volgende manier benaderd worden. Neem een vierkant van 1 bij 1. Als je een dart in dat vierkant gooit op een willekeurige plek, is de waarschijnlijkheid dat de afstand van de dart tot de linkeronderhoek van het vierkant kleiner dan 1 is gelijk aan \(\pi/4\).

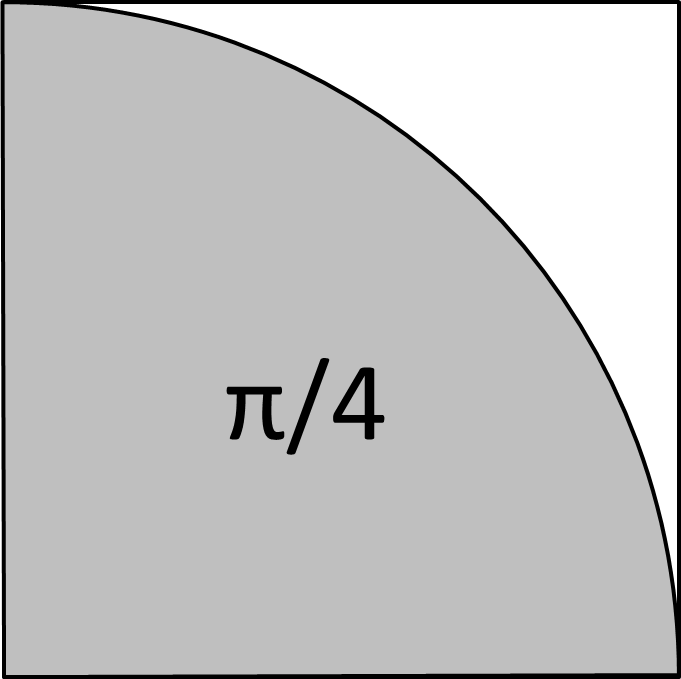
Om dat in te zien, bedenk dat de oppervlakte van een cirkel met straal 1 \(\pi\) is, dus de oppervlakte van een kwart cirkel is \(\pi/4\). Als dus een dart op een willekeurig punt in het vierkant landt, is de waarschijnlijkheid dat die dart in de kwart cirkel landt \(\pi/4\). Als je \(n\) darts in het vierkant werpt, en \(m\) ervan landen in de kwart cirkel, dan benadert \(4m/n\) de waarde \(\pi\) als \(n\) voldoende groot is.

Invoer

Een getal \(n \in \mathbb{N}_0\).

Uitvoer

Simuleer dat er \(n\) darts op een vierkant van 1 bij 1 geworpen worden. Bepaal het aantal darts \(m\) waarvan de afstand tot de linkeronderhoek van het vierkant kleiner dan 1. Schrijf de waarde \(4m/n\) uit.

Tip

Gebruik de random() functie uit de random module.

Tip

De afstand van een punt \((x, y)\) tot de linkeronderhoek kun je berekenen als \(\sqrt{x^2 + y^2}\).

Voorbeeld

Invoer:

100000

Uitvoer:

3.13992