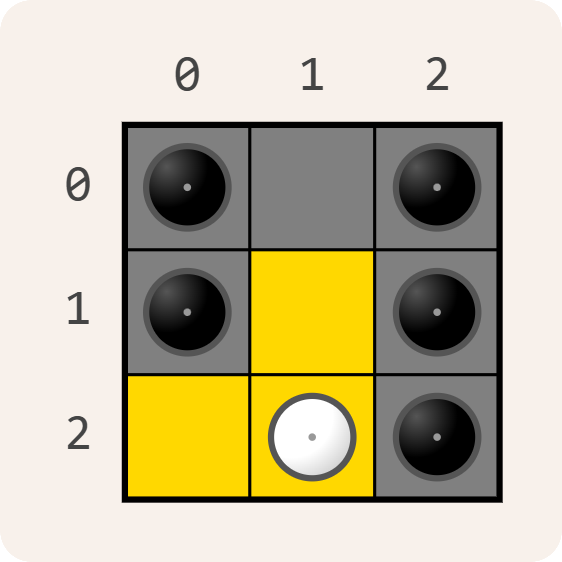
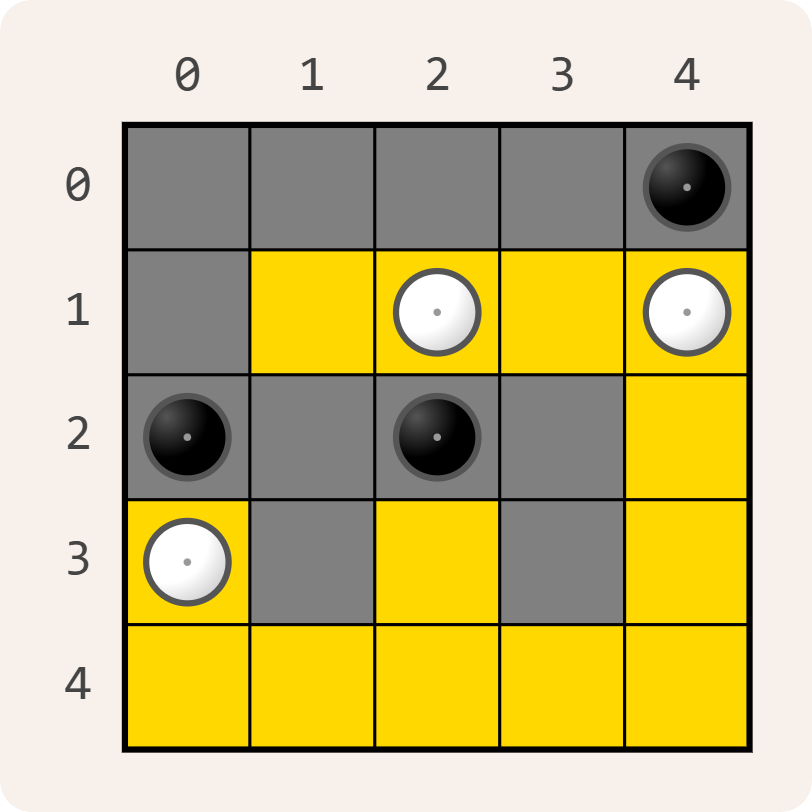
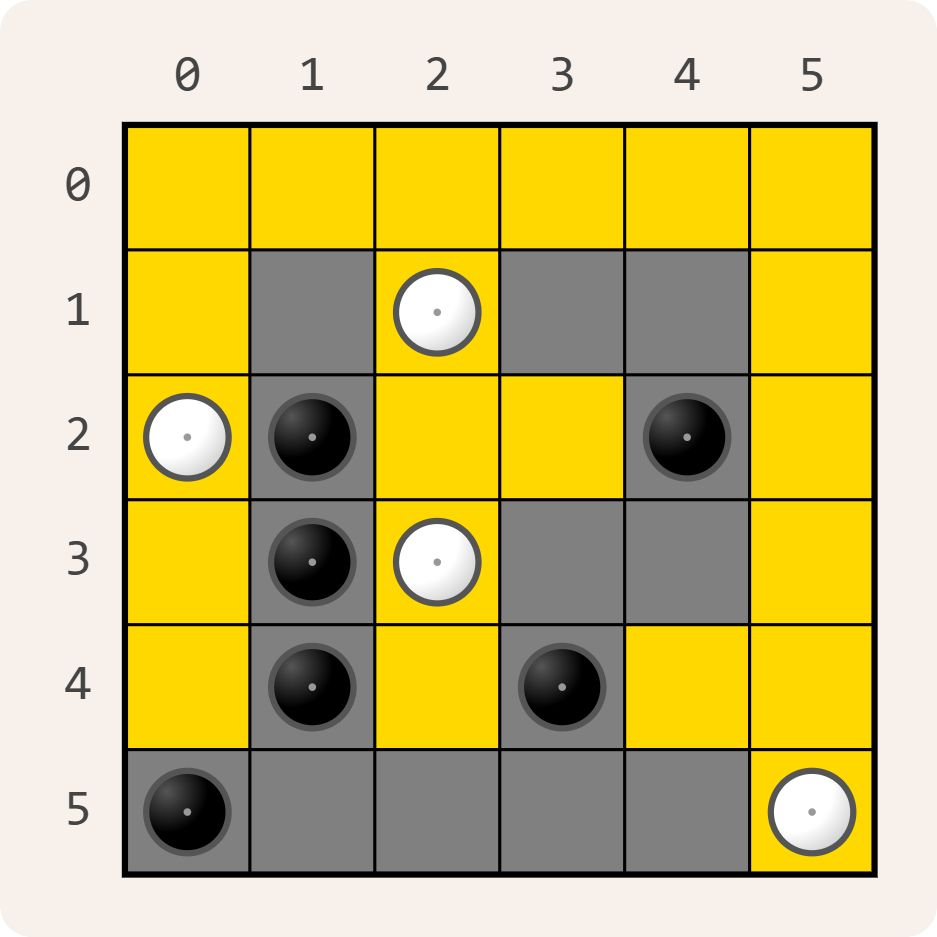
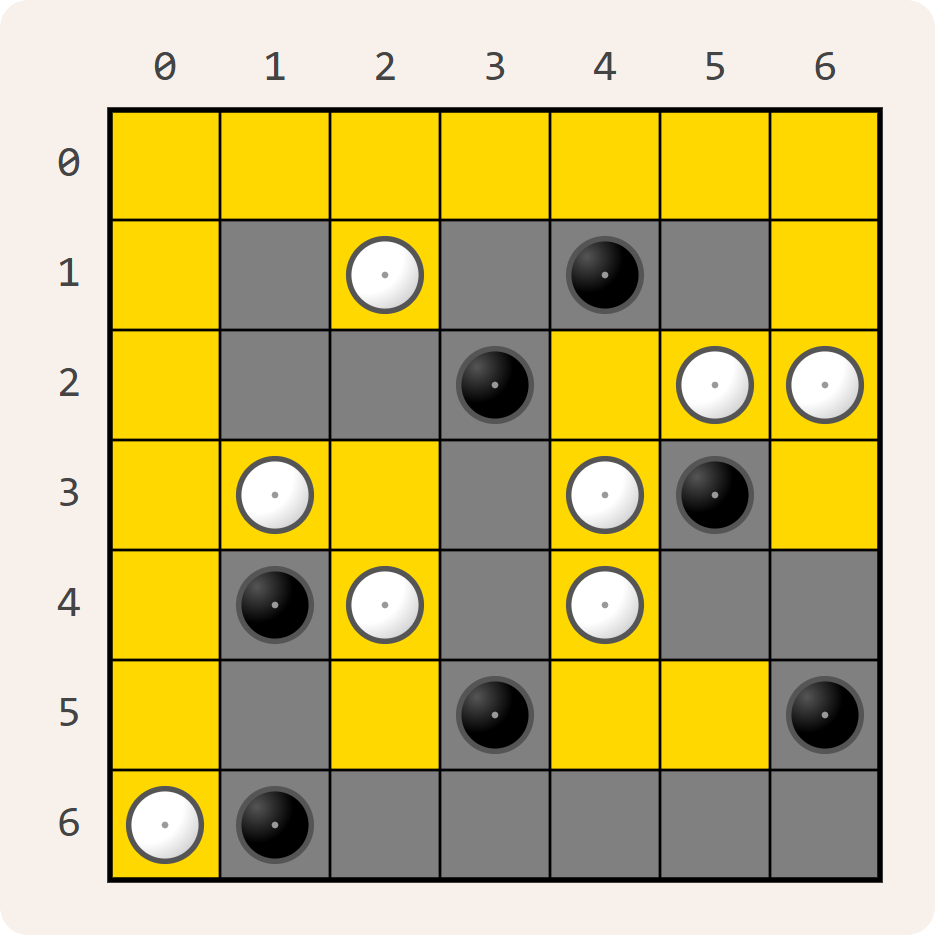
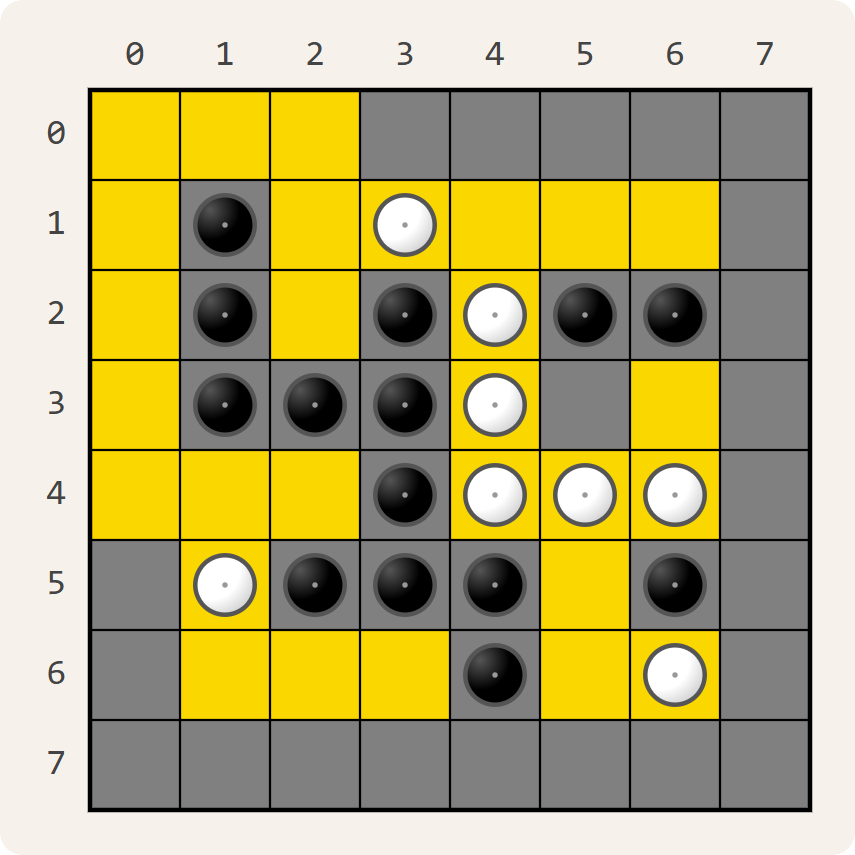
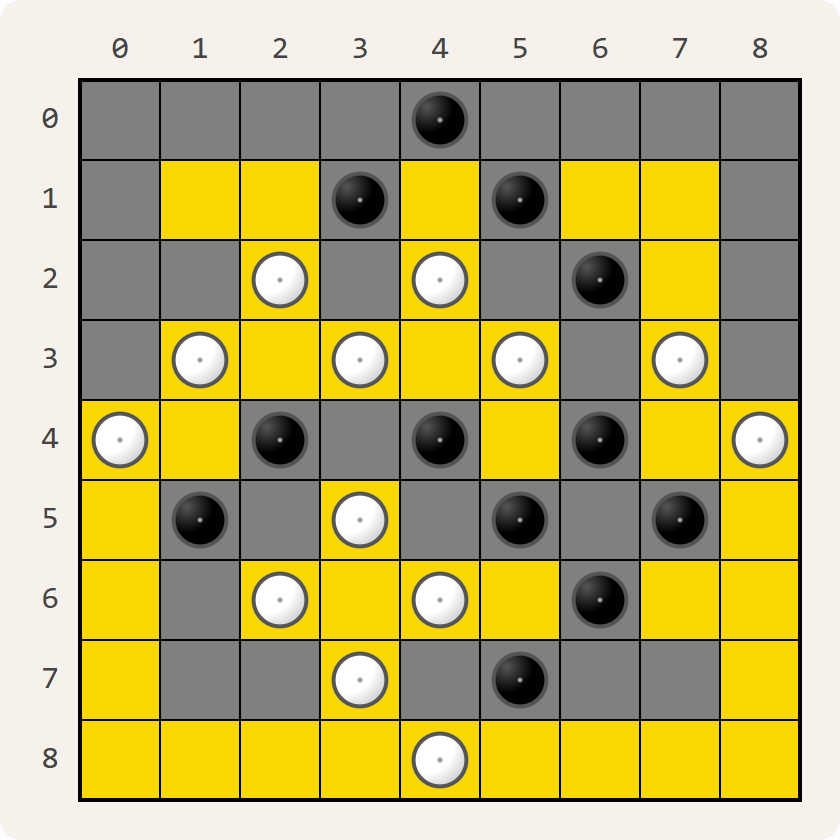
Yin-Yang is een logische puzzel die bestaat uit een vierkant $$n \times n$$ rooster met $$n$$ rijen en $$n$$ kolommen. Bij aanvang zijn sommige vakjes wit of zwart gemarkeerd. Die vakjes kunnen niet van kleur wijzigen. De overige vakjes zijn voorlopig nog leeg.

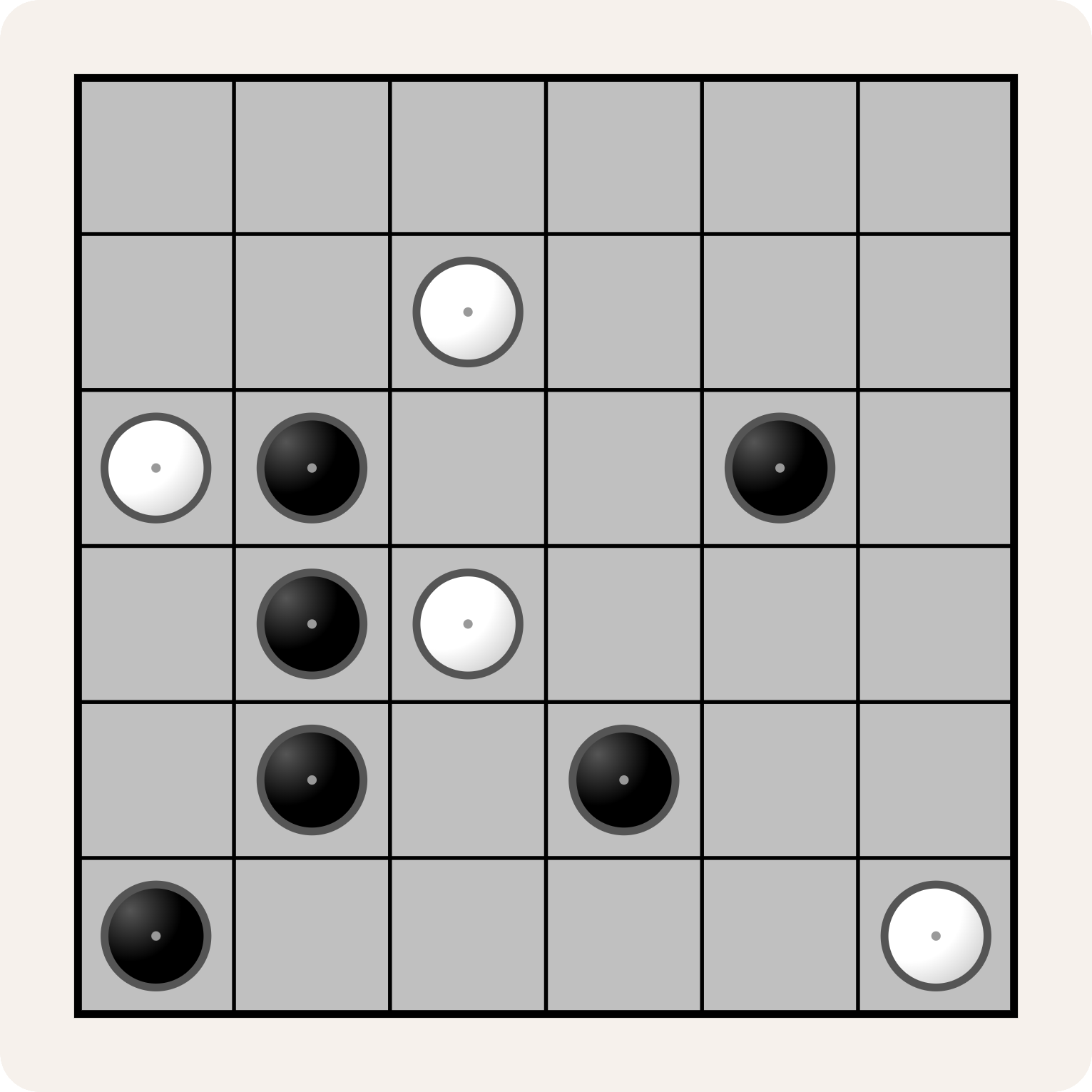
Het doel is om alle lege vakjes wit of zwart te maken zodat

• alle witte vakjes één aaneengesloten gebied vormen

• alle zwarte vakjes één aaneengesloten gebied vormen

• geen enkel $$2 \times 2$$ vierkant bestaat uit vier vakjes met dezelfde kleur

Daarbij worden vakjes van dezelfde kleur door horizontaal en vertikaal aangrenzende zijden verbonden tot aaneengesloten gebieden.

Dit is een oplossing van bovenstaande Yin-Yang puzzel: de witte vakjes vormen één aaneengesloten gebied (aangeduid met een gele achtergrondkleur), de zwarte vakjes vormen één aaneengesloten gebied (aangeduid met een donkergrijze achtergrond), en er is geen enkel $$2 \times 2$$ vierkant dat bestaat uit vier vakjes met dezelfde kleur.

Dit kan geen oplossing zijn van een Yin-Yang puzzel: de witte vakjes vormen wel één aaneengesloten gebied, maar de zwarte vakjes vormen twee aaneengesloten gebieden.

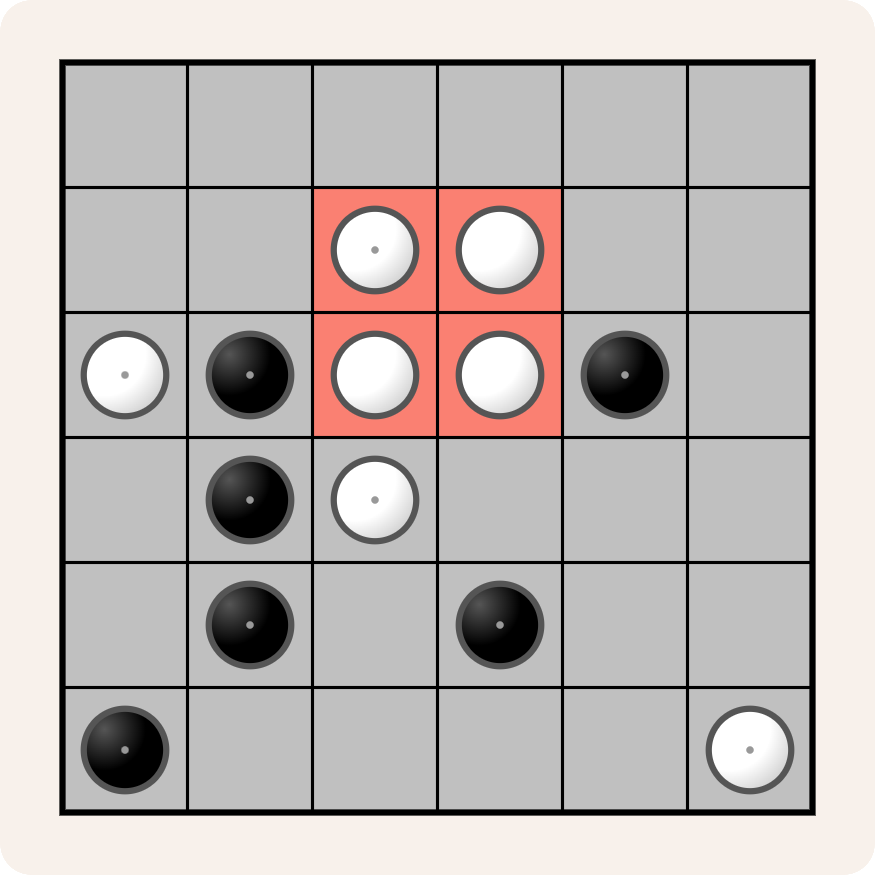
Dit kan ook geen aanzet zijn tot een oplossing van een Yin-Yang puzzel, omdat het $$2 \times 2$$ vierkant aangeduid met een rode achtergrondkleur bestaat uit vier vakjes met dezelfde kleur.

Opgave

We nummeren de rijen in het rooster van een Yin-Yang puzzel van boven naar onder, en de kolommen van links naar rechts, telkens vanaf nul. Zo kunnen we de positie van een vakje in het rooster voorstellen door een tuple $$(r, k)$$, met $$r$$ (int; $$0 \leq r < n$$) het nummer van de rij en $$k$$ (int; $$0 \leq k < n$$) het nummer van de kolom waarop het vakje voorkomt.

Definieer een klasse YinYang waarmee Yin-Yang puzzels met een vierkant $$n \times n$$ rooster kunnen voorgesteld worden. Bij het aanmaken van een nieuwe puzzel $$\mathcal{Y}$$ (YinYang) moeten drie argumenten doorgegeven worden aan deze drie parameters:

1. dimensie (int): de dimensie $$n$$ van het rooster van puzzel $$\mathcal{Y}$$

2. wit (list, tuple of set): een collectie met de posities van vakjes die wit gekleurd zijn in de opgave van puzzel $$\mathcal{Y}$$

3. zwart (list, tuple of set): een collectie met de posities van vakjes die zwart gekleurd zijn in de opgave van puzzel $$\mathcal{Y}$$

Daarbij moeten de volgende voorwaarden voldaan zijn:

• de collecties die worden doorgegeven aan de parameters wit en zwart mogen geen enkele positie gemeenschappelijk hebben (een vakje kan niet tegelijkertijd wit en zwart gekleurd zijn)

• de collecties die worden doorgegeven aan de parameters wit en zwart mogen geen enkele positie bevatten die buiten het rooster van puzzel $$\mathcal{Y}$$ ligt

• de collectie die wordt doorgegeven aan de parameters wit mag geen vier posities bevatten die samen een $$2 \times 2$$ vierkant vormen

• de collectie die wordt doorgegeven aan de parameters zwart mag geen vier posities bevatten die samen een $$2 \times 2$$ vierkant vormen

Als minstens één van deze voorwaarden niet voldaan is, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige puzzel.

Het moet mogelijk zijn om lege vakjes zwart of wit te maken, of vakjes die leeg waren in de opgave van de puzzel terug leeg te maken als die ondertussen zwart of wit gemaakt zijn. Daarom moet je op een puzzel $$\mathcal{Y}$$ (YinYang) minstens de volgende methoden kunnen aanroepen:

• Een methode maak_wit waaraan de positie $$p$$ (tuple) van een vakje moet doorgegeven worden. Als positie $$p$$ buiten het rooster van puzzel $$\mathcal{Y}$$ ligt, als het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$ niet leeg is, of als het wit maken van het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$ een wit $$2 \times 2$$ vierkant zou doen ontstaan, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige actie, en mag het rooster van puzzel $$\mathcal{Y}$$ niet wijzigen. Anders moet het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$ wit gemaakt wordt, en moet een verwijzing naar puzzel $$\mathcal{Y}$$ teruggegeven worden.

• Een methode maak_zwart waaraan de positie $$p$$ (tuple) van een vakje moet doorgegeven worden. Als positie $$p$$ buiten het rooster van puzzel $$\mathcal{Y}$$ ligt, als het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$ niet leeg is, of als het zwart maken van het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$ een zwart $$2 \times 2$$ vierkant zou doen ontstaan, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige actie, en mag het rooster van puzzel $$\mathcal{Y}$$ niet wijzigen. Anders moet het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$ zwart gemaakt wordt, en moet een verwijzing naar puzzel $$\mathcal{Y}$$ teruggegeven worden.

• Een methode maak_leeg waaraan de positie $$p$$ (tuple) van een vakje moet doorgegeven worden. Als positie $$p$$ buiten het rooster van puzzel $$\mathcal{Y}$$ ligt, als het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$ leeg is, of als het vakje op positie $$p$$ wit of zwart was in de opgave van puzzel $$\mathcal{Y}$$, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige actie, en mag het rooster van puzzel $$\mathcal{Y}$$ niet wijzigen. Anders moet het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$ leeg gemaakt wordt, en moet een verwijzing naar puzzel $$\mathcal{Y}$$ teruggegeven worden.

• Een methode aaneengesloten_gebied waaraan de positie $$p$$ (tuple) van een vakje moet doorgegeven worden. Als positie $$p$$ buiten het rooster van puzzel $$\mathcal{Y}$$ ligt of als het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$ leeg is, dan moet de methode een lege verzameling (set) teruggeven. Anders moet de methode een verzameling (set) teruggeven met de posities (tuple) van alle vakjes in het aaneengesloten gebied met vakjes van dezelfde kleur die door horizontaal en vertikaal aangrenzende zijden verbonden zijn met het vakje op positie $$p$$ in het rooster van puzzel $$\mathcal{Y}$$.

  Flood fill

  De methode aaneengesloten_gebied kun je best implementeren met een flood fill algoritme.

  Dit algoritme gebruikt twee verzamelingen: een verzameling $$G$$ met alle posities van het samenhangde gebied en een verzameling $$T$$ met alle posities die nog moeten onderzocht worden. Beide verzamelingen bevatten initieel enkel de positie $$p$$. Daarna blijven we deze procedure herhalen tot verzameling $$T$$ leeg is:

  • kies een willekeurige positie $$t$$ uit $$T$$
  • voor elke naburige positie $$b$$ van positie $$t$$
    • als de vakjes op posities $$b$$ en $$p$$ dezelfde kleur hebben en als positie $$b$$ niet voorkomt in $$G$$
      • voeg positie $$b$$ toe aan $$T$$
      • voeg positie $$b$$ toe aan $$G$$
  • verwijder positie $$t$$ uit $$T$$

  Als verzameling $$T$$ leeg is, dan bevat verzameling $$G$$ alle posities van het aaneengesloten gebied.

• Een methode isopgelost waaraan geen argumenten moeten doorgegeven worden. De methode moet een Booleaanse waarde (bool) teruggeven die aangeeft of de puzzel opgelost werd. We herhalen nog eens dat dat het geval is als er geen lege vakjes meer zijn, als alle witte vakjes één aaneengesloten gebied vormen, als alle zwarte vakjes één aaneengesloten gebied vormen, en als geen enkel $$2 \times 2$$ vierkant bestaat uit vier vakjes met dezelfde kleur.

Als er een puzzel $$\mathcal{Y}$$ (YinYang) wordt doorgegeven aan de ingebouwde functie str, dan moet die een stringvoorstelling (str) van het rooster van puzzel $$\mathcal{Y}$$ teruggeven. Daarin wordt elke rij van het rooster voorgesteld als een afzonderlijke regel, en worden de opeenvolgende vakjes op een rij (van links naar rechts) elk voorgesteld door één karakter:

• W: een vakje dat wit was in de opgave van de puzzel

• w: een vakje dat leeg was in de opgave van de puzzel, en dat wit gemaakt werd

• B: een vakje dat zwart was in de opgave van de puzzel

• b: een vakje dat leeg was in de opgave van de puzzel, en dat zwart gemaakt werd

• -: een vakje dat leeg was in de opgave van de puzzel, en dat nog altijd leeg is of dat terug leeg gemaakt werd

Voorbeeld

In deze interactieve sessie gebruiken we de Yin-Yang puzzel met een $$6 \times 6$$ rooster uit de inleiding als voorbeeld. Daarbij maken we stap voor stap de lege vakjes wit of zwart, tot we de oplossing krijgen die in de inleiding gegeven wordt.

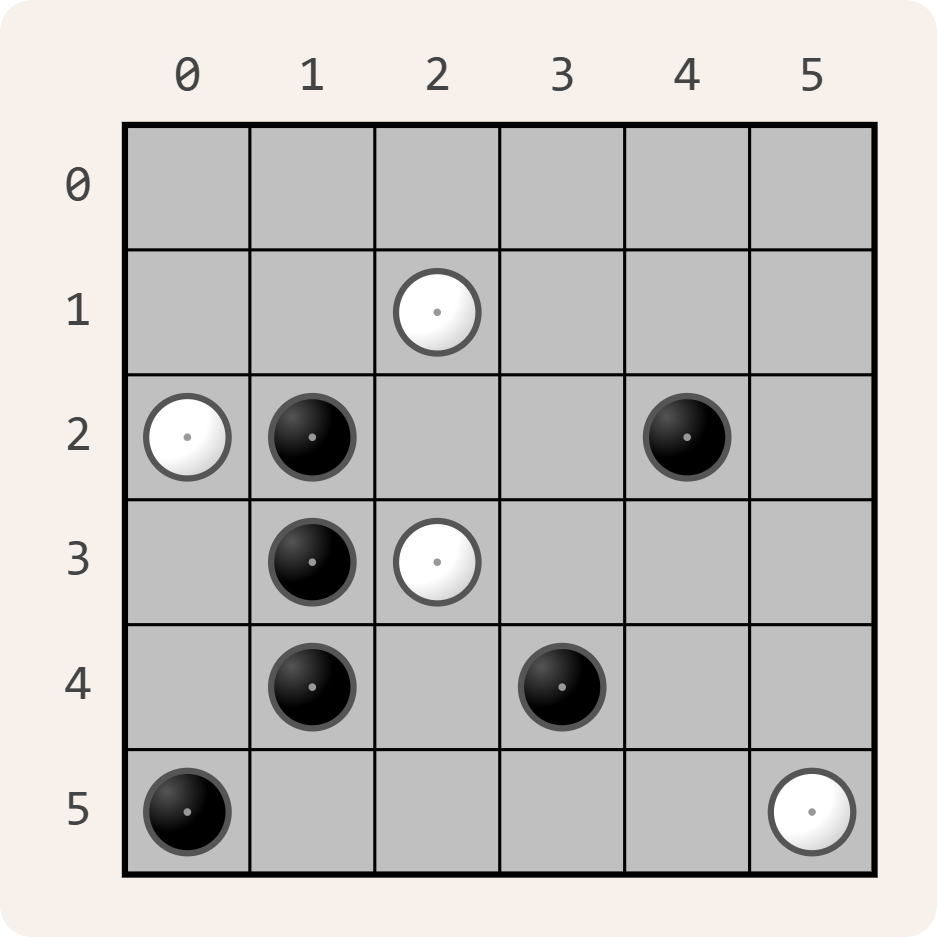
>>> puzzel = YinYang(dimensie=6, wit=[(2, 0), (1, 2), (3, 2), (5, 5)], zwart=[(2, 1), (2, 4), (3, 1), (4, 1), (4, 3), (5, 0)])
>>> print(puzzel)
------
--W---
WB--B-
-BW---
-B-B--
B----W
>>> print(puzzel.maak_wit((0, 0)))
w-----
--W---
WB--B-
-BW---
-B-B--
B----W
>>> puzzel.maak_zwart((3, 2))     # positie is reeds bezet
Traceback (most recent call last):
AssertionError: ongeldige actie
>>> puzzel.maak_zwart((1, 6))     # positie ligt buiten puzzel
Traceback (most recent call last):
AssertionError: ongeldige actie
>>> print(puzzel.maak_zwart((5, 1)))
w-----
--W---
WB--B-
-BW---
-B-B--
Bb---W
>>> puzzel.maak_zwart((4, 0))       # er wordt een vierkant gevormd
Traceback (most recent call last):
AssertionError: ongeldige actie
>>> print(puzzel.maak_wit((0, 1)).maak_wit((0, 2)).maak_wit((0, 3)).maak_wit((0, 4)).maak_zwart((0, 5)))
wwwwwb
--W---
WB--B-
-BW---
-B-B--
Bb---W
>>> print(puzzel.maak_leeg((0, 5)))
wwwww-
--W---
WB--B-
-BW---
-B-B--
Bb---W
>>> print(puzzel.maak_wit((0, 5)))
wwwwww
--W---
WB--B-
-BW---
-B-B--
Bb---W
>>> print(puzzel.maak_wit((1, 0)).maak_zwart((1, 1)).maak_zwart((1, 3)).maak_zwart((1, 4)).maak_wit((1, 5)))
wwwwww
wbWbbw
WB--B-
-BW---
-B-B--
Bb---W
>>> print(puzzel.maak_wit((2, 2)).maak_wit((2, 3)).maak_wit((2, 5)))
wwwwww
wbWbbw
WBwwBw
-BW---
-B-B--
Bb---W
>>> print(puzzel.maak_wit((3, 0)).maak_zwart((3, 3)).maak_zwart((3, 4)).maak_wit((3, 5)))
wwwwww
wbWbbw
WBwwBw
wBWbbw
-B-B--
Bb---W
>>> print(puzzel.maak_wit((4, 0)).maak_wit((4, 2)).maak_wit((4, 4)).maak_wit((4, 5)))
wwwwww
wbWbbw
WBwwBw
wBWbbw
wBwBww
Bb---W
>>> puzzel.isopgelost()
False
>>> print(puzzel.maak_wit((5, 2)).maak_zwart((5, 3)).maak_zwart((5, 4)))
wwwwww
wbWbbw
WBwwBw
wBWbbw
wBwBww
BbwbbW
>>> puzzel.aaneengesloten_gebied((2, 1))
{(2, 1), (3, 1), (1, 1), (5, 1), (5, 0), (4, 1)}
>>> puzzel.aaneengesloten_gebied((3, 2))
{(4, 0), (0, 2), (0, 5), (2, 2), (1, 0), (2, 5), (4, 2), (3, 0), (4, 5), (0, 1), (1, 2), (0, 4), (1, 5), (3, 2), (3, 5), (5, 2), (4, 4), (5, 5), (0, 0), (0, 3), (2, 0), (2, 3)}
>>> puzzel.isopgelost()
False
>>> print(puzzel.maak_leeg((5, 2)).maak_zwart((5, 2)))
wwwwww
wbWbbw
WBwwBw
wBWbbw
wBwBww
BbbbbW
>>> puzzel.aaneengesloten_gebied((2, 1))
{(1, 3), (2, 4), (2, 1), (3, 4), (4, 3), (3, 1), (1, 1), (5, 4), (5, 1), (1, 4), (3, 3), (5, 0), (5, 3), (4, 1), (5, 2)}
>>> puzzel.aaneengesloten_gebied((3, 2))
{(4, 0), (0, 2), (0, 5), (2, 2), (1, 0), (2, 5), (4, 2), (3, 0), (4, 5), (0, 1), (1, 2), (0, 4), (1, 5), (3, 2), (3, 5), (4, 4), (5, 5), (0, 0), (0, 3), (2, 0), (2, 3)}
>>> puzzel.isopgelost()
True

De oplossingen die je indient, worden ook getest aan de hand van deze puzzels.

Bronnen

• Ahmadi A, Khorramian A (2024). Efficient Brute-force state space search for Yin-Yang puzzle. The Journal of Supercomputing 80(3), 3066–3088.

• Demaine ED, Lynch J, Rudoy M, Uno Y (2021). Yin-Yang puzzles are NP-complete.