Een nonogram is een Japanse beeldpuzzel waarbij een verborgen afbeelding moet gevonden worden. Deze afbeelding kan gevormd worden door de vakjes van een rechthoekig rooster zwart of wit te kleuren, rekening houdend met de reeks natuurlijke getallen die voor elke rij en elke kolom van het rooster wordt opgegeven. Deze getallen geven aan hoeveel opeenvolgende zwarte vakjes er op die rij of kolom staan. Als de opgave bijvoorbeeld de getallenreeks 4 8 3 aangeeft, betekent dit dat de rij of kolom bestaat uit reeksen van vier, acht en drie opeenvolgende zwarte vakjes, in die volgorde, en dat er minstens één wit vakje staat tussen elk van deze opeenvolgende reeksen.

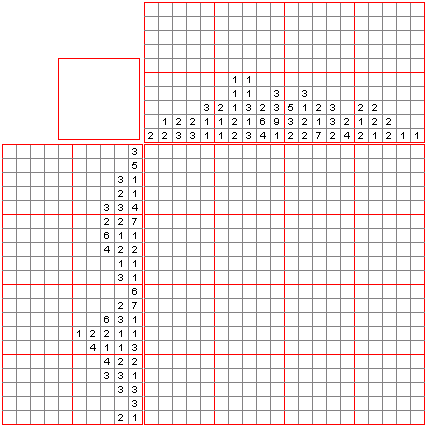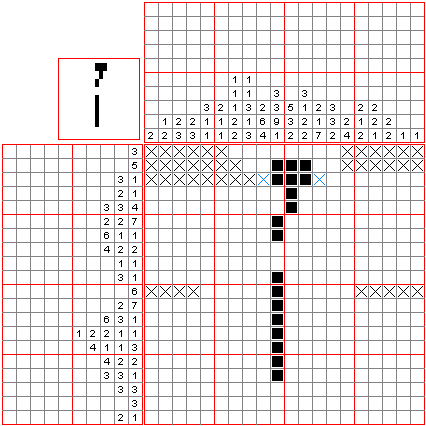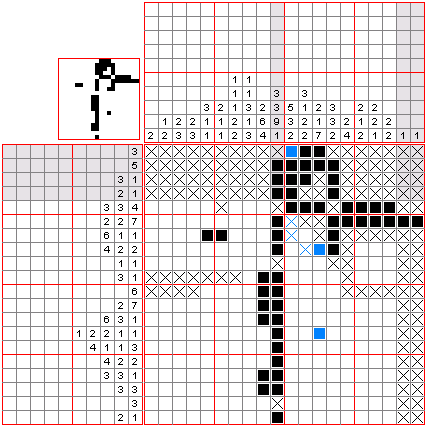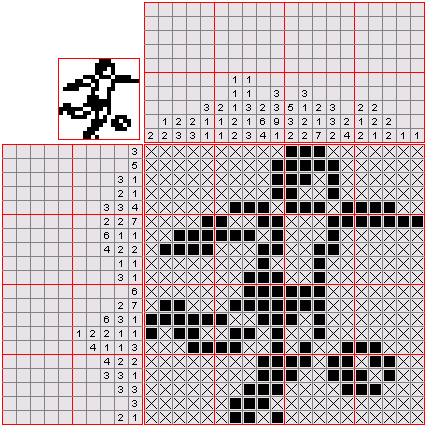
Opgave

Voor deze opgave moet je een vereenvoudigde versie van de nonogrampuzzel oplossen. Zoals bij de originele puzzel worden voor elke rij de reeksen opeenvolgende zwarte vakjes opgegeven. De omschrijving voor de kolommen hebben we echter niet langer nodig. Elke reeks opeenvolgende zwarte vakjes wordt nu immers omschreven door een koppel natuurlijke getallen $$(s, l)$$, waarbij $$s$$ en $$l$$ respectievelijk de startpositie en de lengte van de reeks aangeven. Het meest linkse vakje van een rij staat hierbij op positie nul.

Merk op dat de volgorde waarin de reeksen opeenvolgende zwarte vakjes worden opgegeven nu niet langer een rol speelt. Een rij van een nonogrampuzzel kan dus omschreven worden door een reeks getallenparen die respectievelijk de startpositie en de lengte van de reeks opeenvolgende zwarte vakjes aangeven.

Invoer

De invoer omschrijft de opgave van een vereenvoudigde nonogrampuzzel. De eerste regel van de invoer bevat twee natuurlijke getallen $$h$$ en $$b$$ die respectievelijk de hoogte en de breedte van de afbeelding aangeven. De twee getallen worden van elkaar gescheiden door één enkele spatie. Daarna volgen $$h$$ regels die telkens een volgende regel van de verborgen afbeelding omschrijven. Deze omschrijving bestaat uit koppels natuurlijke getallen: elk koppel bestaat uit twee natuurlijke getallen, van elkaar gescheiden door een komma en ingesloten tussen ronde haakjes. De koppels zelf worden telkens van elkaar gescheiden door een komma. Behalve tussen de cijfers van eenzelfde natuurlijk getal, mogen binnen de omschrijving voorts op elke plaats spaties staan. Het eerste en tweede getal van elk koppel geven respectievelijk de startpositie en de lengte aan van een reeks opeenvolgende zwarte vakjes op de regel van de afbeelding.

Uitvoer

Schrijf de verborgen afbeelding uit die omschreven wordt door de invoer. Deze afbeelding is een rechthoekig $$h \times b$$ rooster waarvan de witte vakjes voorgesteld worden door spaties en de zwartje vakjes door hekjes (#). Het totaal aantal spaties en hekjes van elke regel moet gelijk zijn aan $$b$$.

Voorbeeld

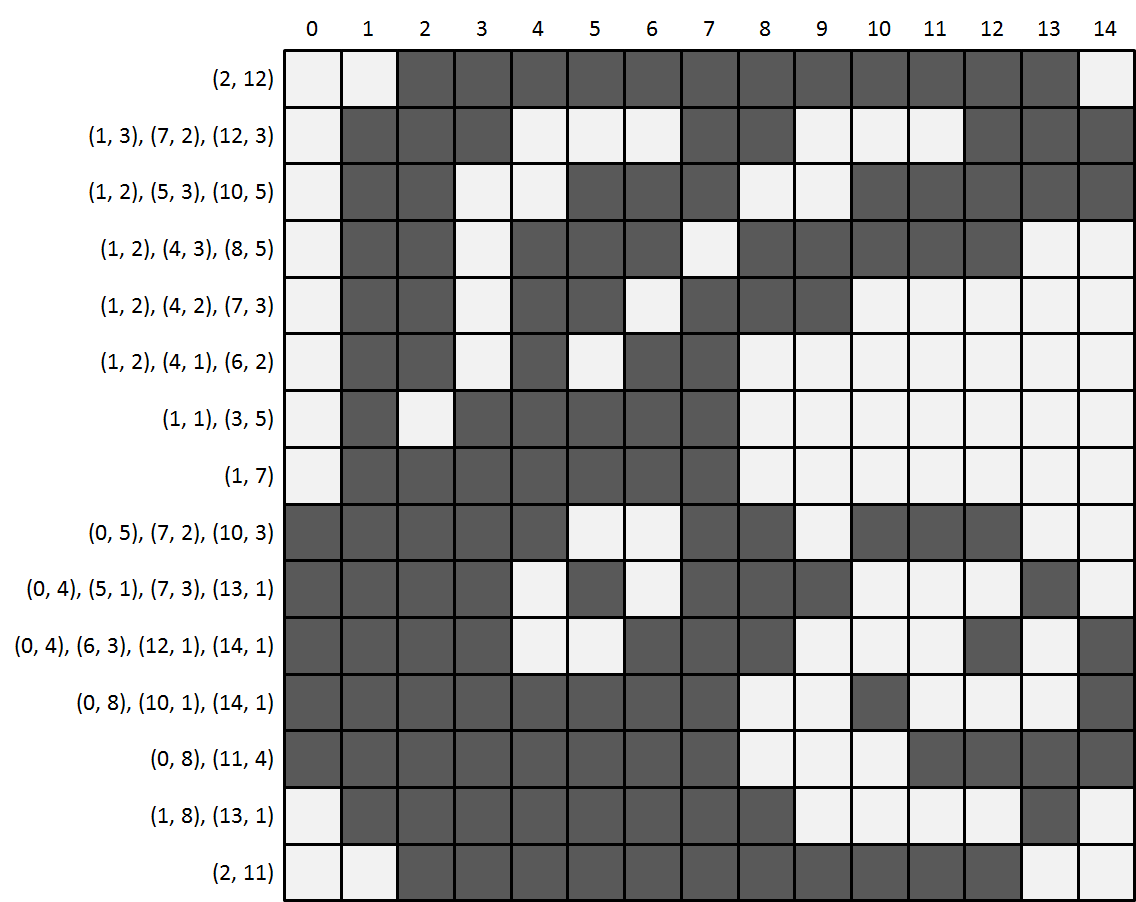
Invoer:

15 15
(2, 12)
(1, 3), (7, 2), (12, 3)
(1, 2), (5, 3), (10, 5)
(1, 2), (4, 3), (8, 5)
(1, 2), (4, 2), (7, 3)
(1, 2), (4, 1), (6, 2)
(1, 1), (3, 5)
(1, 7)
(0, 5), (7, 2), (10, 3)
(0, 4), (5, 1), (7, 3), (13, 1)
(0, 4), (6, 3), (12, 1), (14, 1)
(0, 8), (10, 1), (14, 1)
(0, 8), (11, 4)
(1, 8), (13, 1)
(2, 11)

Uitvoer:

  ############ 
 ###   ##   ###
 ##  ###  #####
 ## ### #####  
 ## ## ###     
 ## # ##       
 # #####       
 #######       
#####  ## ###  
#### # ###   # 
####  ###   # #
########  #   #
########   ####
 ########    # 
  ###########