Deze opgave is een eerbetoon aan de grootste Japanse guru, bedenker en verzamelaar van raadsels Nobuyuki Yoshigahara (芦ヶ原 伸之 ,1936–2004). Dit genie in het oplossen van puzzels — die bij iedereen in Japan bekend staat onder de naam Nob — behaalde een diploma in de toegepaste chemie aan het Tokyo Institute of Technology. Na een korte en ietwat ontgoochelende onderzoekscarrière in de polymeerchemie, stortte hij zich volledig op het lesgeven van chemie en wiskunde in het middelbaar onderwijs.

Het hele oeuvre van grootmeester Nob laat zich ontzettend moeilijk in een notendop vatten, omdat de veelzijdigheid van zijn verwezenlijken en zijn vindingrijkheid nauwelijks hun gelijke kennen. Nob had een grote passie voor getallen, en de volgende vernuftige puzzel wordt algemeen beschouwd als één van zijn meesterwerken.
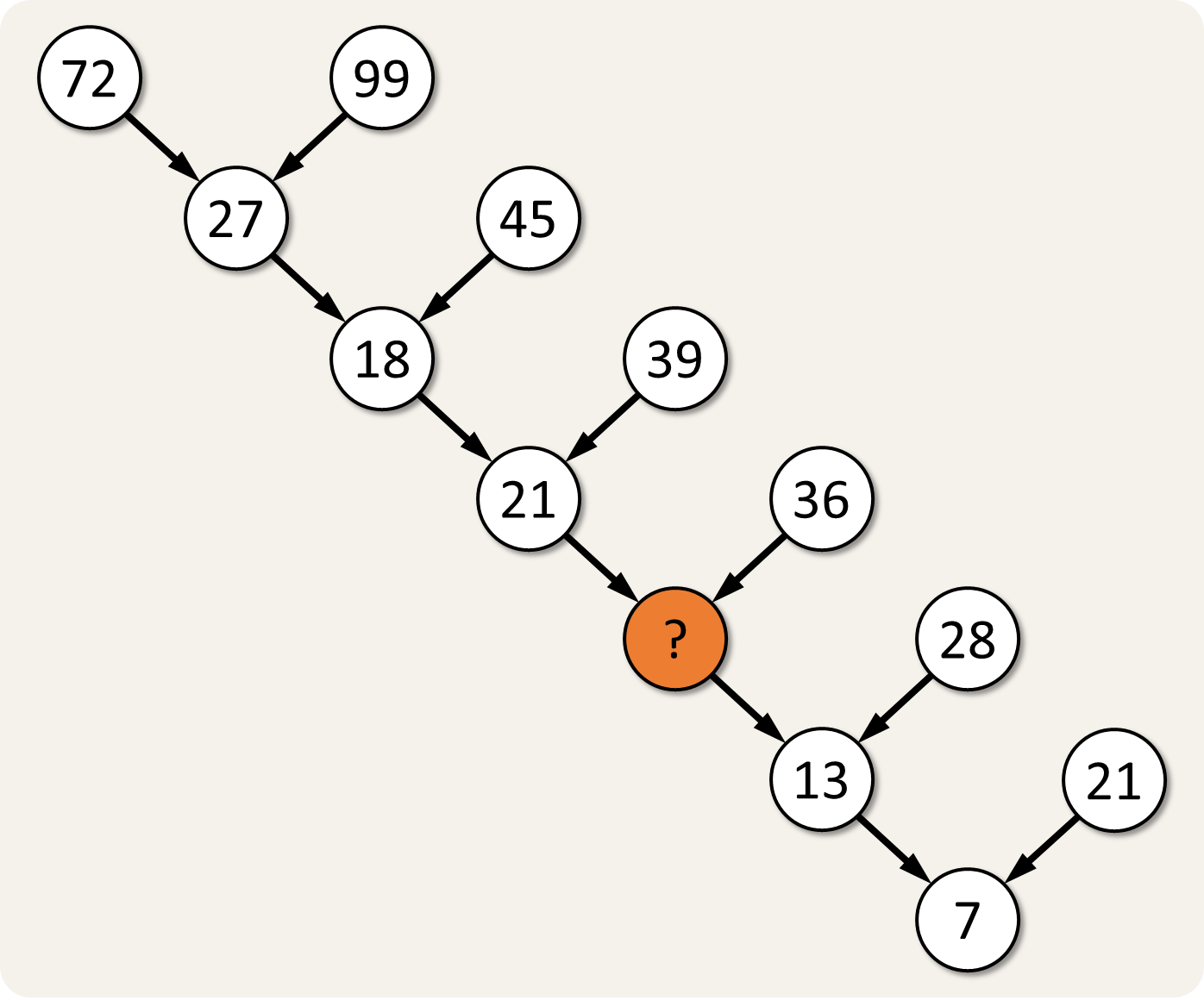
Deze puzzel is briljant in zijn eenvoud: welk getal ontbreekt op de plaats van het vraagteken? Of zoals Lee Sallows1 het omschrijft:
Je moet deze puzzel zelf oplossen, anders zal je er nooit de schoonheid van inzien.
Denk vooral maar niet te snel dat je het antwoord gevonden hebt en dat er een typfout in de opgave geslopen is. De reeds ingevulde getallen zijn wel degelijk correct.
Op het eerste gezicht is het heel verleidelijk om te denken dat het getal 15 moet ingevuld worden op de plaats van het vraagteken. Helaas klopt het patroon dat het onderste getal telkens het verschil is tussen het rechtse getal en het linkse getal erboven niet met het onderste getal 7 in de boom.
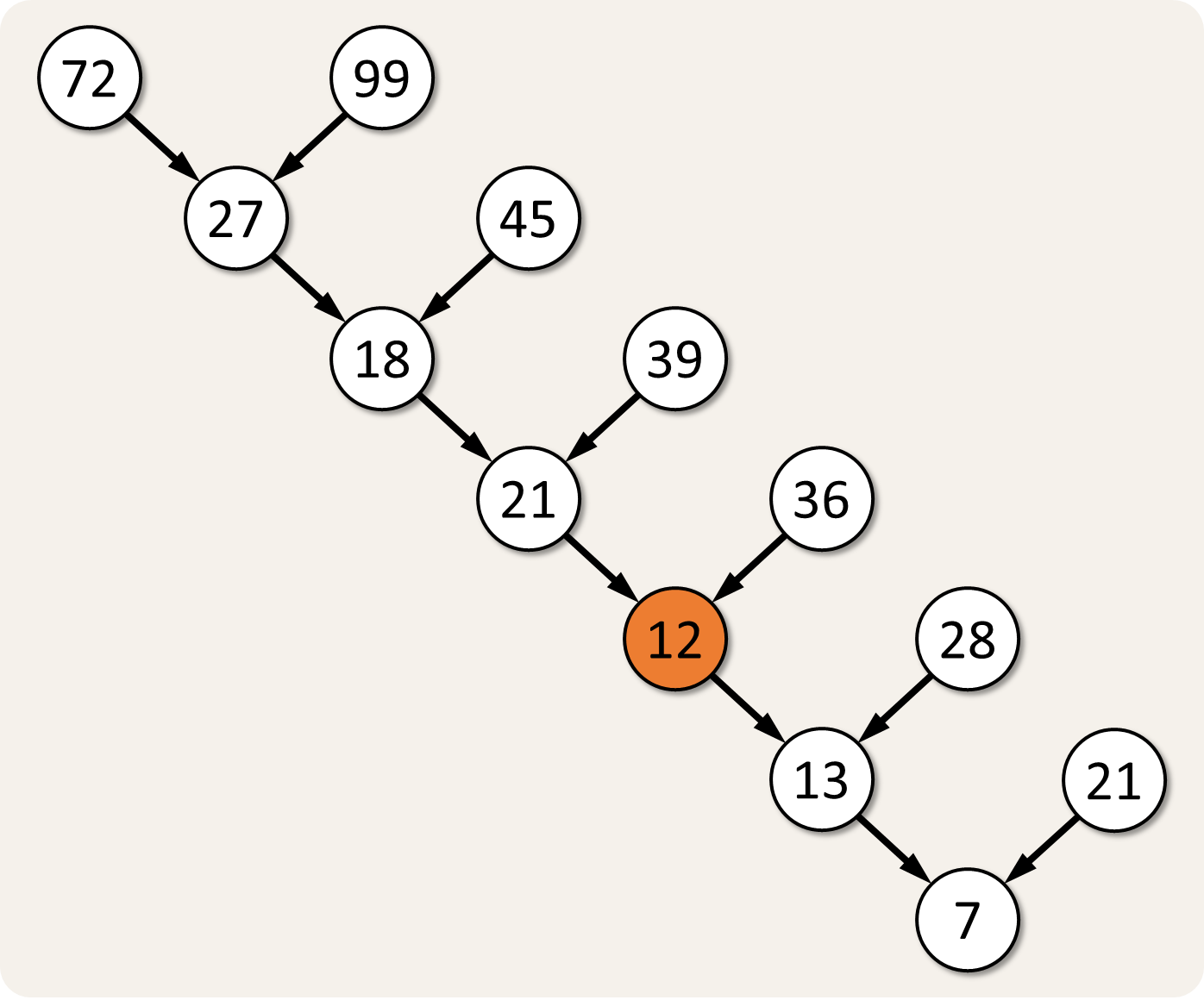
Je moest wel degelijk een ander patroon zien te vinden dat klopt voor alle getallen die reeds in de boom werden ingevuld. Elk onderste getal is namelijk gelijk aan de som van de cijfers van de twee getallen erboven. Zo geven de bovenste twee getallen de som $$7 + 2 + 9 + 9$$ met als resultaat het getal $$27$$ in de cirkel eronder. Op dezelfde manier kunnen we het ontbrekende getal berekenen: $$2 + 1 + 3 + 6 = 12$$.
Invoer
De invoer bestaat uit een reeks natuurlijke getallen, elk op een afzonderlijke regel. Deze reeks bevat minstens één getal en wordt afgesloten door het getal -1, dat zelf geen deel uitmaakt van de reeks.
Uitvoer
De gegeven getallen vormen de bovenste getallen uit een boom zoals die gebruikt wordt in het bovenstaande raadsel van Nob Yoshigahara. Voor onderstaand voorbeeld staat de reeks getallen uit de invoer hieronder ingekleurd in het groen.
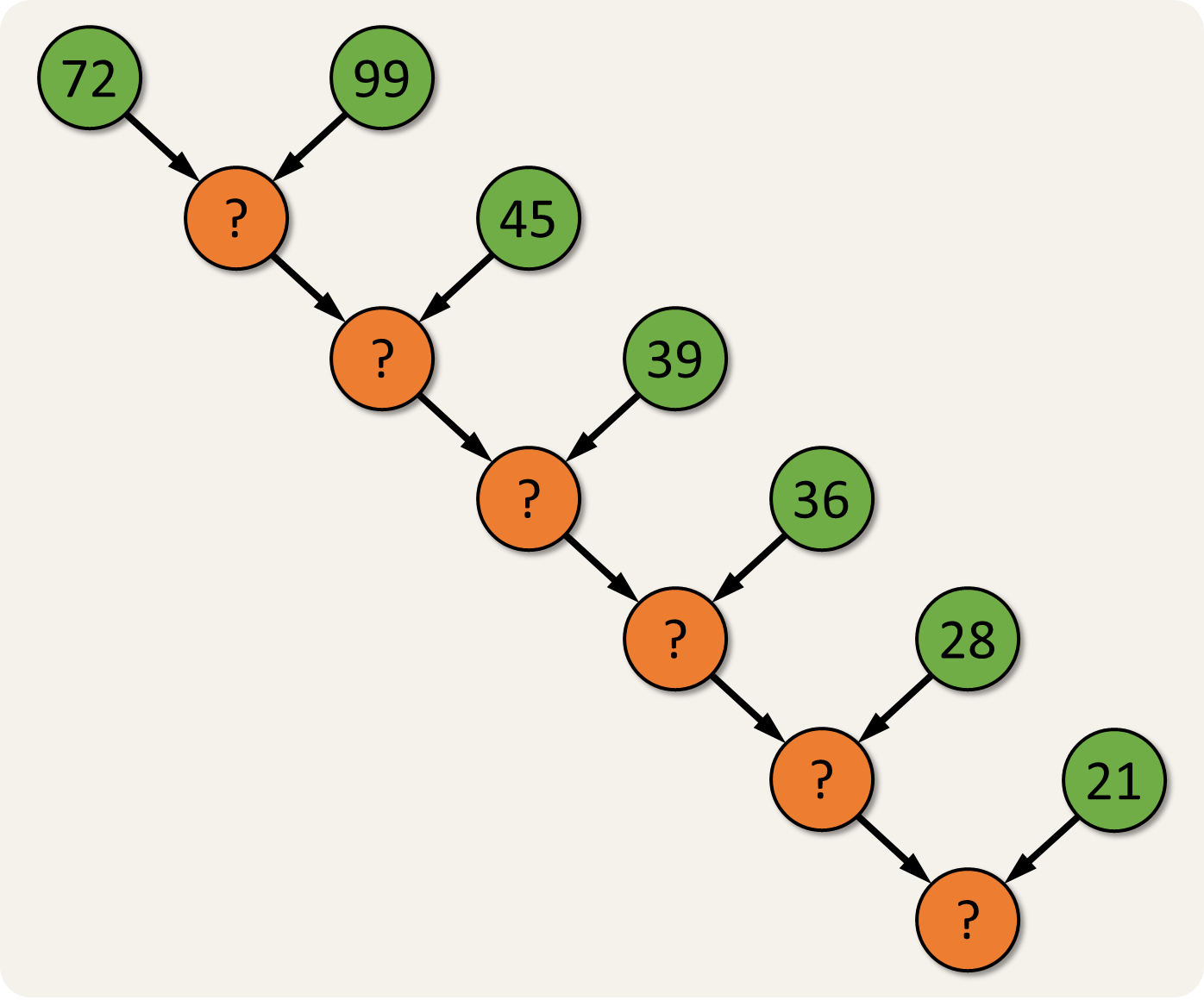
Je opdracht bestaat erin om de boom verder aan te vullen door de getallen te berekenen die op de oranje posities moeten ingevuld worden. Deze getallen kan je vinden door telkens de som van de cijfers te bepalen van de twee getallen die erboven staan.
De uitvoer moet op de volgende manier opgemaakt worden. Op elke regel staan er twee getallen uit de boom. Op de eerste regel is er geen insprong, en elke volgende regel begint met een insprong die telkens twee spaties groter is dan de insprong op de vorige regel. Daarna moeten de twee getallen uitgeschreven worden, waarbij elk getal gecentreerd wordt over vier posities. Aan het einde van een regel mogen er geen spaties staan.
Voorbeeld
Invoer:
72
99
45
39
36
28
21
-1Uitvoer:
72 99
27 45
18 39
21 36
12 28
13 21
7