Het Oog van Horus — het alziende oog — werd in het oude Egypte gebruikt als symbool voor bescherming, goddelijke kracht en goede gezondheid. Het oog wordt verpersoonlijkt in de vrouwelijke zonnegodin Wadjet. De afzonderlijke onderdelen van het oog staan voor ruiken, zien, denken, horen, proeven en voelen. Men gaat ervan uit dat de oude Egyptenaren deze onderdelen gebruikten als voorstelling voor één gedeeld door de eerste zes machten van twee, zoals aangegeven in onderstaande figuur.

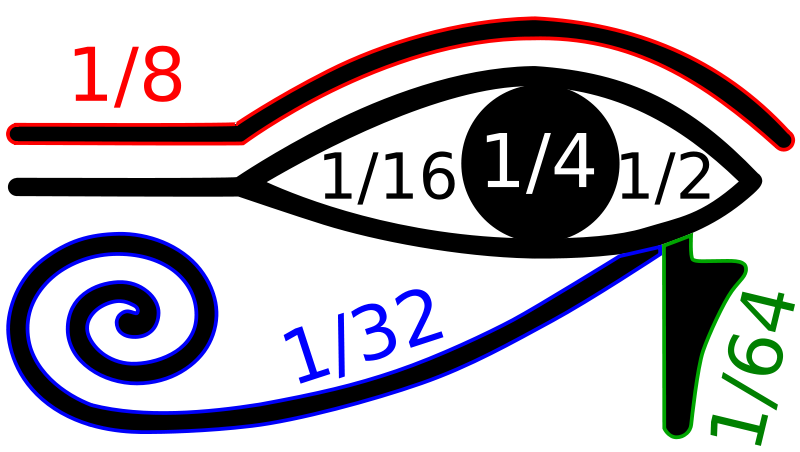
Een Egyptische breuk is een som van verschillende eenheidsbreuken, zoals $$\frac{1}{2} + \frac{1}{3} + \frac{1}{16}$$. Daarbij heeft elke breuk in de uitdrukking een teller die gelijk is aan 1 en een natuurlijk getal als noemer. Alle breuken hebben bovendien een verschillende noemer. De waarde van een dergelijke uitdrukking is een positief rationaal getal $$\frac{a}{b}$$. Zo sommeert bovenstaande Egyptische breuk bijvoorbeeld tot $$\frac{43}{48}$$. Het is bewezen dat elk positief rationaal getal kan geschreven worden als een Egyptische breuk.

De oude Egyptenaren gebruikten sommen van dit type om rationale getallen te noteren, en verschillende andere volkeren bleven ze gebruiken tot laat in de middeleeuwen. De Rhind-papyrus¹ uit 500 voor Christus maakt reeds melding van Egyptische breuken als een "oude methode" en er wordt gedacht dat ze teruggaan tot de tijd van de allereerste piramiden. Het bekende boek Liber Abaci² van Leonardo de Pisa uit 1215 na Christus — dat Europese wiskundigen concepten bijbracht zoals het getal nul, het Hindu-Arabische talstelsel, en de wereldberoemde konijnenrij³ (Fibonacci was het pseudoniem van Leonardo) — beschrijft ook hoe breuken op deze manier kunnen ontbonden worden. In de moderne wiskunde hebben Egyptische breuken plaats moeten ruimen voor gewone breuken en de decimale voorstelling van rationale getallen.

Een eenvoudige manier om een gegeven breuk te schrijven als een Egyptische breuk bestaat erin om telkens de grootste eenheidsbreuk te nemen die nog in de breuk past, deze van de breuk af te trekken om te berekenen wat nog rest, en dit te blijven herhalen totdat de resterende breuk een eenheidsbreuk is. Aangezien bijvoorbeeld 7 gedeeld door 15 kleiner is dan $$\frac{1}{2}$$ maar groter is dan $$\frac{1}{3}$$, is de eerste eenheidsbreuk gelijk aan $$\frac{1}{3}$$ en is de eerste rest gelijk aan $$\frac{2}{15}$$. Daarna volgt dat $$\frac{2}{15}$$ kleiner is dan $$\frac{1}{7}$$ maar groter dan $$\frac{1}{8}$$, waardoor de tweede eenheidbreuk gelijk is aan $$\frac{1}{8}$$ en de tweede rest gelijk aan $$\frac{1}{120}$$. Deze laatste breuk is zelf een eenheidsbreuk, waardoor we klaar zijn met de ontbinding: \[\frac{7}{15} = \frac{1}{3} + \frac{1}{8} + \frac{1}{120}\] Tijdens deze berekeningen maken we steeds gebruik van de meest vereenvoudigde vorm van een breuk $$\frac{a}{b}$$. Een breuk is in zijn meest vereenvoudigde vorm als de teller $$a$$ en noemer $$b$$ geen gemeenschappelijke delers hebben. De meest vereenvoudigde vorm kan dus gevonden worden door teller en noemer te delen door de grootste gemeenschappelijke deler (ggd) van beide getallen.

De ggd van twee natuurlijke getallen kan berekend worden aan de hand van de gcd functie uit de fractions module van de Python Standard Library.

>>> from fractions import gcd
>>> gcd(20, 8)
4

Er bestaan nog andere algoritmen om een gegeven breuk als een Egyptische breuk te ontbinden, maar er bestaat geen algoritme dat altijd een grootste aantal termen of een kleinst mogelijke noemer garandeert. Zo resulteert het gretige algoritme dat hierboven werd beschreven bijvoorbeeld in \[\frac{5}{121} = \frac{1}{25} + \frac{1}{757} + \frac{1}{763309} + \frac{1}{873960180913} + \frac{1}{1527612795642093418846225}\] terwijl er een eenvoudigere ontbinding van dezelfde breuk bestaat onder de vorm \[\frac{5}{121} = \frac{1}{33} + \frac{1}{121} + \frac{1}{363}\]

Opmerking

Zorg ervoor dat je in deze opgave rekent met breukvormen, waarbij de teller en de noemer beide gehele getallen vormen. Als je gaat werken met floating point getallen om te rekenen met een decimale voorstelling van de breuken, dan zal je in de problemen raken omwille van de afrondingsfouten die hierbij optreden.

Invoer

Een breuk $$\frac{a}{b}$$, waarbij de teller $$a \in \mathbb{N_0}$$ en de noemer $$b \in \mathbb{N_0}$$ elk op een afzonderlijke regel staan. Je mag ervan uitgaan dat $$0 < \frac{a}{b} \leq 1$$.

Uitvoer

De lijst van noemers van de ontbinding van de breuk $$\frac{a}{b}$$ als een Egyptische breuk, die resulteert als het gretige algoritme wordt toegepast dat hierboven werd beschreven. De noemers moeten van klein naar groot opgelijst worden, elk op een afzonderlijke regel.

Voorbeeld

Invoer:

47
60

Uitvoer:

2
4
30

Voorbeeld

Invoer:

7
15

Uitvoer:

3
8
120

Voorbeeld

Invoer:

5
41

Uitvoer:

9
93
11439