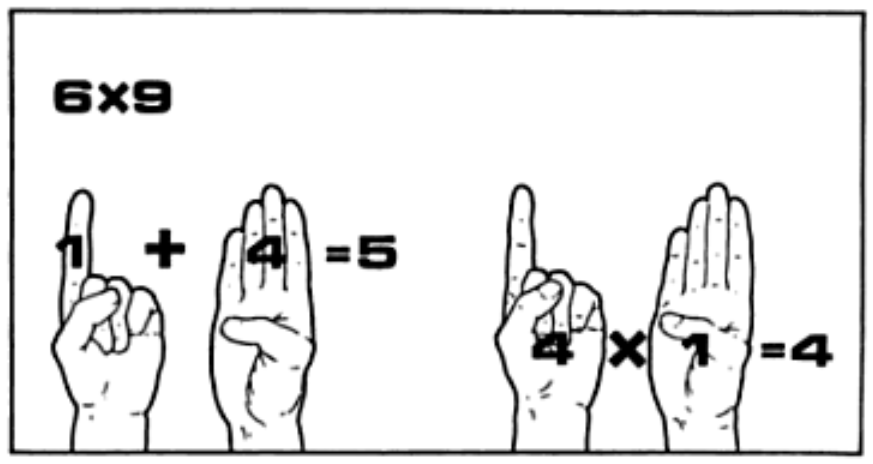
In de Middeleeuwen gebruikte men een handige vingertechniek om snel te kunnen vermenigvuldigen. Om bijvoorbeeld de vermenigvuldiging $$6 \times 9$$ uit te rekenen, steek je één vinger van je linkerhand op om het verschil aan te geven tussen de vijf vingers aan die hand en het eerste getal dat moet vermenigvuldigd worden. Van de rechterhand steek je vier vingers op, namelijk het verschil tussen 9 en 5.
Daarna tel je het aantal opgestoken vingers van beide handen bij elkaar op en vermenigvuldig je het resultaat met 10 \[ 10 \times (1 + 4) = 50 \] Daarbij tel je het product op van de gesloten vingers van de twee handen \[ 50 + 4 \times 1 = 54 \] Dit geeft je het gevraagde resultaat. Deze methode laat toe om het product van twee getallen tussen 6 en 9 te berekenen terwijl je enkel de vermenigvuldigingstabel tot en met $$5 \times 5$$ moet kennen en ook moet kunnen vermenigvuldigen met 10.
Om twee getallen tussen 10 en 15 met elkaar te vermenigvuldigen kan je een gelijkaardige methode gebruiken. Om bijvoorbeeld de vermenigvuldiging $$14 \times 12$$ uit te rekenen steek je vier vingers van de linkerhand en twee vingers van de rechterhand op. Daarna tel je het aantal opgestoken vingers op, vermenigvuldig je het resultaat met 10 en telt er 100 bij op \[ 100 + 10 \times (4 + 2) = 160 \] Daarbij tel je het product op van de opgestoken vingers \[ 160 + (4 \times 2) = 168 \] Ook in dit geval moet je enkel kunnen vermenigvuldigen met tien en de vermenigvuldigingstabel kennen tot en met $$5 \times 5$$.
Beide vingertechnieken zijn een direct gevolg van het feit dat voor de vermenigvuldiging van twee natuurlijke getallen $$x$$ en $$y$$ de volgende algemene formule geldt \[ xy = 100 + 10 [(x - 10) + (y - 10)] + (x - 10)(y - 10) \]
Invoer
Twee getallen $$x, y \in \mathbb{N}$$ ($$0 \leq x, y \leq 20$$) die elk op een afzonderlijke regel staan.
Uitvoer
Een regel die illustreert hoe de twee getallen met elkaar kunnen vermenigvuldigd worden op basis van de vingertechnieken die in de inleiding uitgelegd worden. Hierbij moet onderscheid gemaakt worden tussen de volgende gevallen:
-
als beide getallen kleiner of gelijk zijn aan 5 of als minstens één van beide getallen 10 is dan moet het product rechtstreeks berekend worden (zie eerste voorbeeld)
-
als beide getallen tussen 6 en 9 liggen (inclusief grenzen) dan moet het product berekend worden op basis van de eerste methode die beschreven wordt in de inleiding (zie tweede voorbeeld)
-
als beide getallen tussen 11 en 15 liggen (inclusief grenzen) dan moet het product berekend worden op basis van de tweede methode die beschreven wordt in de inleiding (zie derde voorbeeld)
-
voor alle andere gevallen moet de algemene formule gebruikt worden voor de berekening van het product (zie vierde voorbeeld)
Bekijk onderstaande voorbeelden om te achterhalen hoe de uitvoer precies moet opgemaakt worden.
Voorbeeld
geval: beide getallen zijn kleiner of gelijk aan 5
Invoer:
2
5Uitvoer:
2 x 5 = 10Voorbeeld
geval: beide getallen liggen tussen 6 en 9 (grenzen inbegrepen)
Invoer:
6
9Uitvoer:
6 x 9 = 10 x (1 + 4) + (4 x 1) = 54Voorbeeld
geval: beide getallen liggen tussen 11 en 15 (grenzen inbegrepen)
Invoer:
14
12Uitvoer:
14 x 12 = 100 + 10 x (4 + 2) + (4 x 2) = 168Voorbeeld
geval: algemene formule om het product van twee natuurlijke getallen te berekenen
Invoer:
4
11Uitvoer:
4 x 11 = 100 + 10 x (-6 + 1) + (-6 x 1) = 44