Een ijskern is een cilindervormig monster afkomstig van een ijskap, meestal uit de poolgebieden of van een gletsjer. Aangezien ijskappen zich vormen door de opeenstapeling van jaarlijkse sneeuwlagen, zijn ze opgebouwd uit ijs van verschillende jaren waarbij de onderste lagen ouder zijn dan de bovenste. Door analyse van de eigenschappen van het ijs en de gassamenstelling van gekristalliseerde luchtbelletjes die in het ijs ingesloten zitten, kan een klimatologische reconstructie gemaakt worden van de periode waarin de ijskern gevormd werd. Op basis van de concentraties en de isotopen van koolstofmonoxide en methaan kan men bijvoorbeeld de evolutie van de lokale temperatuur en de atmosferische samenstelling in kaart brengen.

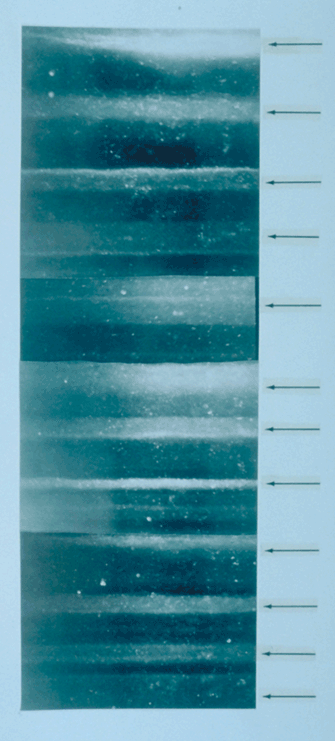
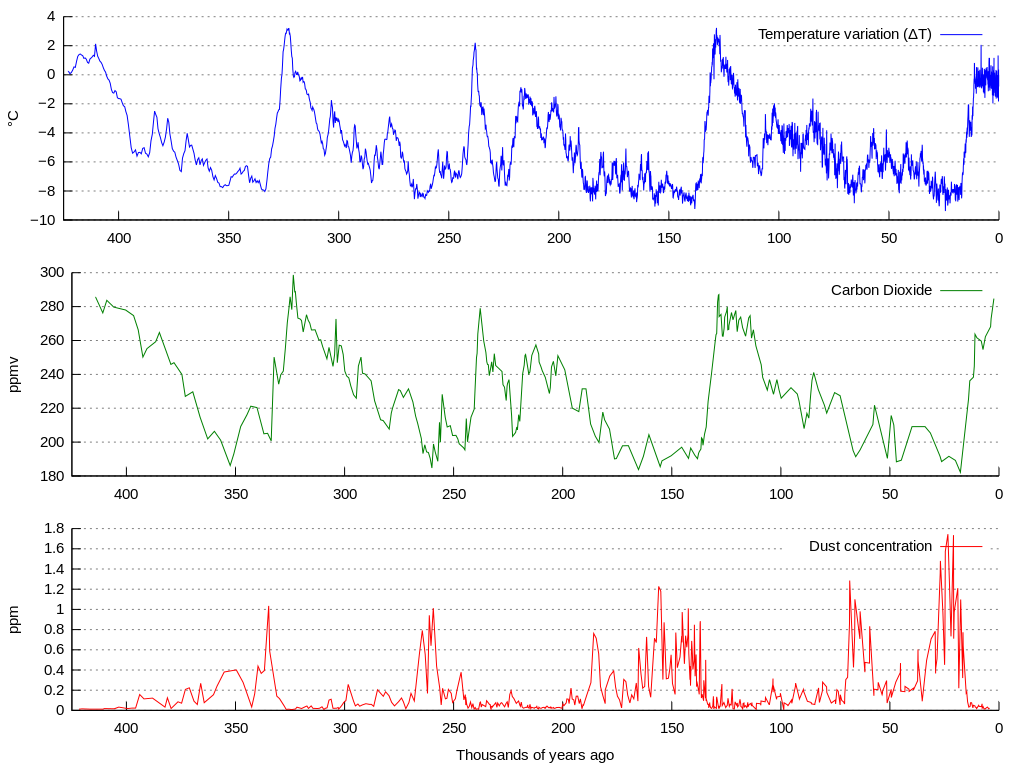
Bovenstaande figuur toont de evolutie van de temperatuur (blauw), de concentratie koolstofdioxide (groen) en de hoeveelheid stofdeeltjes die zich in het ijs hebben vastgezet (rood) in de ijskap van Vostok (Antarctica) over een periode van de laatste 420.000 jaar. Hierin kunnen met het blote oog reeds een aantal klimatologische cycli herkend worden. Het verloop van dergelijke tijdsreeksen bevat echter te veel ruis om ze rechtstreeks door een computer te laten analyseren. Deze ruis kan onderdrukt worden door toepassing van eenvoudige wiskundige technieken om de curves af te vlakken.

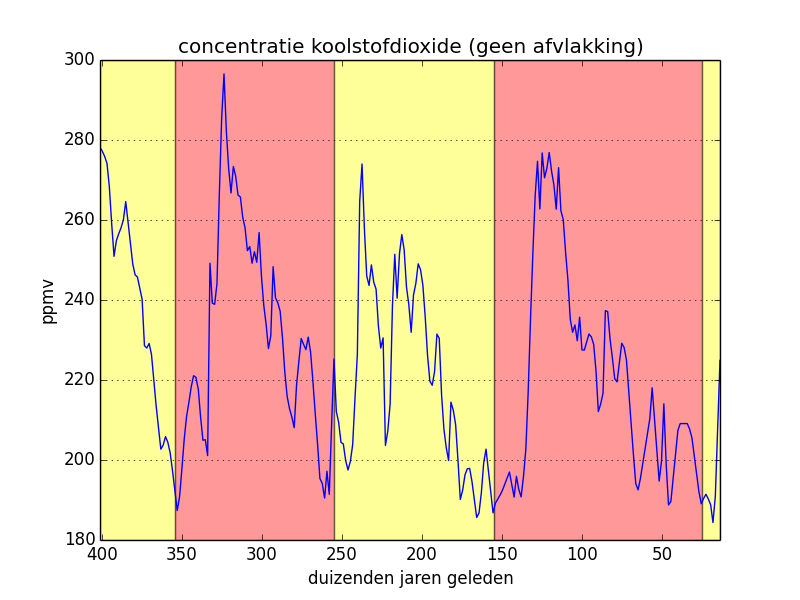
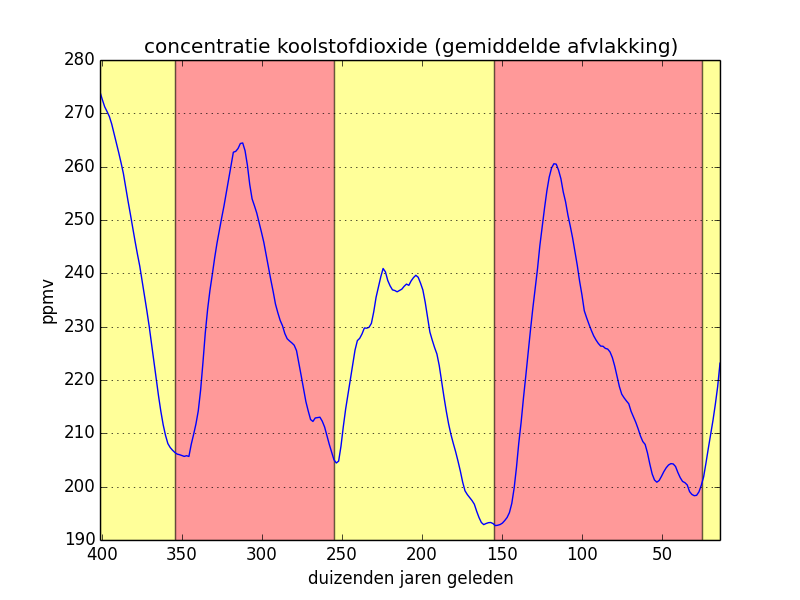
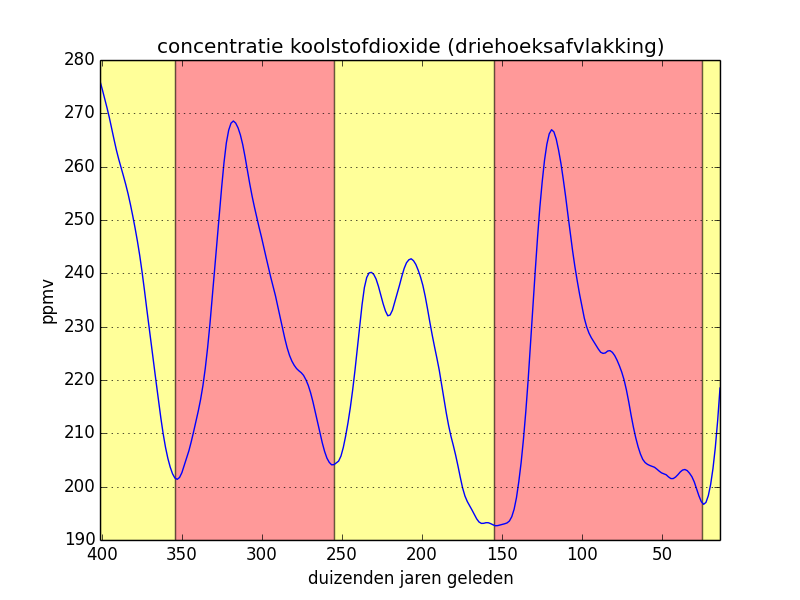
In de linker figuur hieronder hebben de we originele meetwaarden van de concentratie koolstofmonoxide overgenomen, en daarbij hebben we ook de opeenvolgende klimatologische cycli aangeduid. In de middelste figuur hebben we een gemiddelde afvlakking toegepast op de originele meetwaarden en de rechter figuur is het resultaat van een driehoeksafvlakking. In de laatste twee gevallen is het periodieke karakter van de curve nog duidelijker uitgesproken.

Opgave

Langs opeenvolgende punten van een ijskern hebben we de concentratie van een bepaalde eigenschap (bv. de concentratie koolstofdioxide) bepaald. De waarden op deze meetpunten werden gebundeld in een lijst of een tuple. Gevraagd wordt om deze meetwaarden af te vlakken zodat ze makkelijker met de computer kunnen geanalyseerd worden. Hiervoor ga je als volgt te werk:

• Stel dat we beschikken over een reeks van $$m \in \mathbb{N}_0$$ opeenvolgende meetwaarden $$x_i \in \mathbb{R}$$ ($$1 \leq i \leq m$$). Het gewogen gemiddelde $$s$$ van deze meetwaarden wordt bekomen door aan elke meetwaarde een gewicht $$w_i \in \mathbb{R}$$ ($$1 \leq i \leq m$$) te koppelen, en de volgende berekening uit te voeren \[s = \frac{\displaystyle\sum_{i=1}^m w_i x_i}{\displaystyle\sum_{i=1}^m w_i}\] Voor de reeks meetwaarden $$(4, 3, 7)$$ en de reeks gewichten $$(1, 2, 1)$$ is het gewogen gemiddelde dus gelijk aan \[ s = \frac{4 \times 1 + 3 \times 2 + 7 \times 1}{1 + 2 + 1} = 4.25 \] Schrijf een functie gewogenGemiddelde waaraan twee lijsten of tuples moeten doorgegeven worden. Deze argumenten stellen respectievelijk een reeks meetwaarden $$x_i$$ ($$1 \leq i \leq m$$) en een reeks gewichten $$w_i$$ ($$1 \leq i \leq m$$) voor. Indien de gegeven reeksen niet even lang zijn, dan moet de functie een AssertionError opwerpen met de boodschap reeksen moeten even lang zijn. Anders moet de functie het gewogen gemiddelde $$s$$ van de gegeven meetwaarden teruggeven, op basis van de gegeven gewichten.

• Schrijf een functie afvlakken waaraan twee lijsten of tuples moeten doorgegeven worden. Het eerste argument stelt een reeks van $$n \in \mathbb{N}_0$$ opeenvolgende meetwaarden $$x_i \in \mathbb{R}$$ ($$1 \leq i \leq n$$) voor, en het tweede argument een reeks van $$m \in \mathbb{N}_0$$ gewichten $$w_i \in \mathbb{R}$$ ($$1 \leq i \leq m$$). De functie moet als resultaat een nieuwe lijst teruggeven, die de gewogen gemiddelden bevat van alle $$m$$ opeenvolgende meetwaarden met de gegeven gewichten (zie onderstaande figuur). 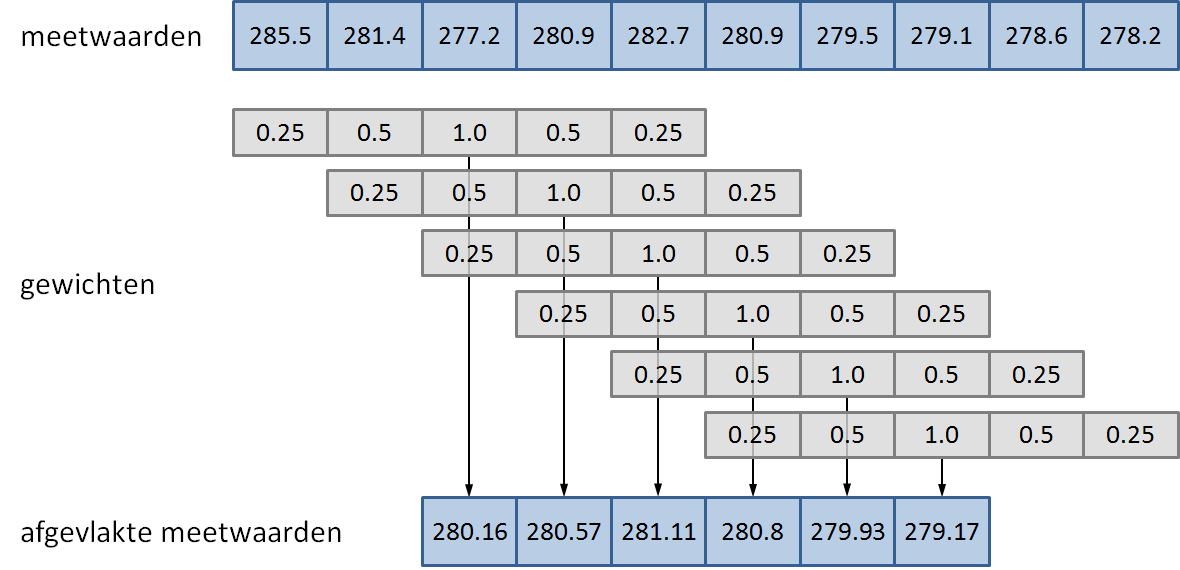Indien geldt dat $$n < m$$, dan moet de lege lijst teruggegeven worden.
  

  

• Als alle gewichten die gebruikt worden bij het afvlakken eenzelfde waarde $$w$$ ($$w \neq 0$$) hebben, dan is het gewogen gemiddelde niets anders dan een gewoon gemiddelde van een meetwaarde en een aantal naburige meetwaarden links en rechts van het meetpunt. Als we bijvoorbeeld de lijst van gewichten [1, 1, 1, 1, 1] gebruiken, dan worden 5 meetwaarden uitgemiddeld (meetpunt en twee punten links en rechts). Dit wordt gemiddelde afvlakking genoemd met vensterbreedte $$v = 5$$. Analoog wordt bij gemiddelde afvlakking met vensterbreedte $$v = 7$$ de lijst gewichten [1, 1, 1, 1, 1, 1, 1] gebruikt. Gebruik de functie afvlakken om een functie afvlakkenGemiddelde te schrijven waaraan verplicht een lijst of tuple van meetwaarden en optioneel een vensterbreedte $$v$$ (argument venster; standaardwaarde 5) moeten doorgegeven worden. De functie moet als resultaat de afgevlakte lijst van meetwaarden teruggeven die resulteert na toepassing van gemiddelde afvlakking met vensterbreedte $$v$$.

• Bij driehoeksafvlakking wordt gebruikgemaakt van een reeks gewichten die in het eerste deel oploopt vanaf 1, en halverwege terug begint af te lopen. Zo maakt driehoeksafvlakking met vensterbreedte $$v=5$$ gebruik van de gewichten [1, 2, 3, 2, 1], gebruikt driehoeksafvlakking met vensterbreedte $$v=7$$ de gewichten [1, 2, 3, 4, 3, 2, 1], enzoverder. Gebruik de functie afvlakken om een functie afvlakkenDriehoek te schrijven waaraan verplicht een lijst of tuple van meetwaarden en optioneel een vensterbreedte $$v$$ (argument venster; standaardwaarde 5) moeten doorgegeven worden. Indien de gegeven vensterbreedte even is, moet de functie een AssertionError opwerpen met boodschap vensterbreedte moet oneven zijn. Anders moet de functie als resultaat de afgevlakte lijst van meetwaarden teruggeven die resulteert na toepassing van driehoeksafvlakking met vensterbreedte $$v$$.

Voorbeeld

In onderstaande interactieve sessie hebben we de floating point getallen afgerond om de voorbeelden beknopt te houden. In de opgave wordt niet gevraagd om een dergelijke afronding uit te voeren.

>>> CO2 = [285.5, 281.4, 277.2, 280.9, 282.7]
>>> gewichten = [0.5, 1.0, 0.5]
>>> gewogenGemiddelde(CO2, gewichten)
Traceback (most recent call last):
AssertionError: reeksen moeten even lang zijn
>>> gewichten = [0.25, 0.5, 1.0, 0.5, 0.25]
>>> gewogenGemiddelde(CO2, gewichten)
280.16
>>> gewogenGemiddelde((4.0, 3.0, 7.0), (1.0, 2.0, 1.0))
4.25

>>> CO2 = [285.5, 281.4, 277.2, 280.9, 282.7, 280.9, 279.5, 279.1, 278.6, 278.2]
>>> afvlakken(CO2, gewichten)
[280.16, 280.57, 281.11, 280.8, 279.93, 279.17]
>>> afvlakkenGemiddelde(CO2)
[281.54, 280.62, 280.24, 280.62, 280.16, 279.26]
>>> afvlakkenGemiddelde(CO2, venster=4)
[281.25, 280.55, 280.425, 281.0, 280.55, 279.525, 278.85]
>>> afvlakkenDriehoek(CO2)
[280.489, 280.533, 280.933, 280.789, 279.978, 279.178]
>>> afvlakkenDriehoek(CO2, venster=4)
Traceback (most recent call last):
AssertionError: vensterbreedte moet oneven zijn
>>> afvlakkenDriehoek(CO2, venster=3)
[281.375, 279.175, 280.425, 281.8, 281.0, 279.75, 279.075, 278.625]

Bronnen

• Petit JR, Jouzel J, Raynaud D, Barkov NI, Barnola JM, Basile I, Bender M, Chappellaz J, Davis M, Delaygue G, Delmotte M, Kotlyakov VM, Legrand M, Lipenkov VY, Lorius C, Pépin L, Ritz C, Saltzman E, Stievenard M (1999). Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 399, 429-436. ¹

• Jouzel J, Petit JR, Souchez R, Barkov NI, Lipenkov VY, Raynaud D, Stievenard M, Vassiliev NI, Verbeke V, Vimeux F (1999). More than 200 meters of lake ice above subglacial Lake Vostok, Antarctica. Science 286(5447), 2138-2141. ²