Beslissingsfouten
Aangezien de beslissing over het al dan niet verwerpen van de nulhypothese bepaald wordt door slechts een steekproef te observeren, kunnen volgende beslissing genomen worden:
| Besluit | H0 | H1 |
|---|---|---|
| Aanvaard H0 | OK | Type II (β) |
| Verwerp H0 | Type I (α) | OK |
Het schema geeft de vier mogelijke situaties:
-
\(H_0\) is in werkelijkheid waar, en dit wordt ook besloten aan de hand van de statistische test (dus geen beslissingsfout)
-
\(H_1\) is in werkelijkheid waar, en dit wordt ook besloten aan de hand van de statistische test (dus geen beslissingsfout)
-
\(H_0\) is in werkelijkheid waar, maar aan de hand van de statistische test wordt besloten om \(H_0\) te verwerpen en \(H_1\) te concluderen. Dus \(H_1\) wordt foutief besloten. Dit is een zogenaamde type I fout.
-
\(H_1\) is in werkelijkheid waar, maar aan de hand van de statistische test wordt besloten om \(H_0\) te aanvaarden. Dit is een zogenaamde type II fout. Dus \(H_0\) wordt foutief aanvaard.
De beslissing is gebaseerd op een teststatistiek \(T\) die een toevalsveranderlijke is. De beslissing is dus ook stochastisch en aan de vier mogelijke situaties uit bovenstaand schema kunnen dus probabiliteiten toegekend worden. Net zoals voor het afleiden van de steekproefdistributie van de teststatistiek, moeten we de distributie van de steekproefobservaties kennen alvorens het stochastisch gedrag van de beslissingen te kunnen beschrijven. Indien we aannemen dat \(H_0\) waar is, dan is de distributie van \(T\) gekend en kunnen ook de kansen op de beslissingen bepaald worden voor de eerste kolom van de tabel.
Type I fout
We starten met de kans op een type I fout (hier uitgewerkt voor het captopril voor beeld):
\[\text{P}\left[\text{type I fout}\right]=\text{P}\left[\text{verwerp }H_0 \mid H_0\right] = \text{P}_0\left[T<t_{n-1;1-\alpha}\right]=\alpha.\]Dit geeft ons meteen een interpretatie van het significantieniveau \(\alpha\): het is de kans op het maken van een type I fout. De constructie van de statistische test garandeert dus dat de kans op het maken van een type I fout gecontroleerd wordt op het significantieniveau \(\alpha\). De kans op het correct aanvaarden van \(H_0\) is dus \(1-\alpha\). Verder kan aangetoond worden dat de p-waarde onder \(H_0\) uniform verdeeld is. Het leidt dus tot een uniforme beslissingsstrategie.
We illustreren dit in een simulatiestudie
- n=15
- \(\mu=0\) mmHg, er is dus geen effect van de behandeling
- \(\sigma =9\) mmHg
- 1000 gesimuleerde steekproeven
nsim <- 10000
n <- 15
sigma <- 9
mu <- 0
mu0 <- 0
alpha <- 0.05
#simulate nsim samples of size n
deltaSim <- matrix(
rnorm(n*nsim,mu,sigma),
nrow=n,
ncol=nsim)
pSim <- apply(
deltaSim,
2,
function(x, mu, alternative)
t.test(x,
mu = mu,
alternative = alternative)$p.value,
mu = mu0,
alternative="less"
)
mean(pSim<alpha)
## [1] 0.0513
pSim %>%
as.data.frame %>%
ggplot(aes(x=.)) +
geom_histogram() +
xlim(0,1)
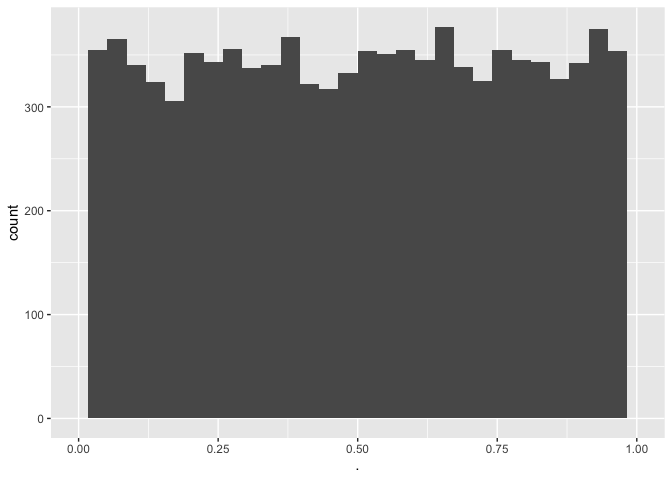
- De type I-fout is inderdaad ongeveer 0,05
- De p-waarden zijn uniform
Opdracht:
Voer de simulatiestudie opnieuw uit verdubbel hierbij het aantal observaties in de steekproef. Wat observeer je?
Type II fout
Het bepalen van de kans op een type II fout is minder evident omdat de alternatieve hypothese minder éénduidig is als de nulhypothese. In het captopril voorbeeld is \(H_1: \mu<0\); met deze informatie wordt de distributie van de steekproefobservaties niet volledig gespecifieerd en dus ook niet de distributie van de teststatistiek. Dit impliceert dat we eigenlijk de kans op een type II fout niet kunnen berekenen. De klassieke work-around bestaat erin om één specifieke distributie te kiezen die voldoet aan \(H_1\).
\[H_1(\delta): \mu=0-\delta \text{ voor een }\delta>0.\]De parameter \(\delta\) kwantificeert de afwijking van de nulhypothese.
De kracht van een test (Engels: power) is een kans die meer frequent gebruikt wordt dan de kans op een type II fout \(\beta\). De kracht wordt gedefinieerd als
\[\pi(\delta) = 1-\beta(\delta) = \text{P}_\delta\left[T>t_{n-1;1-\alpha}\right]=\text{P}_\delta\left[P<\alpha\right].\]De kracht van een niveau-\(\alpha\) test voor het detecteren van een afwijking \(\delta\) van het gemiddelde onder de nulhypothese \(\mu_0=0\) is dus de kans dat de niveau-\(\alpha\) test dit detecteert wanneer de afwijking in werkelijkheid \(\delta\) is.
Merk op dat \(\pi(0)=\alpha\) en de kracht van een test toeneemt als de afwijking van de nulhypothese toeneemt.
De kracht van de test (d.i. de kans om Type II fouten te vermijden) wordt typisch niet gecontroleerd, tenzij d.m.v. studiedesign en steekproefgrootte.
Interpretatie
Stel dat we voor een gegeven dataset bekomen dat \(p<\alpha\), m.a.w. \(H_0\) wordt verworpen. Volgens het schema van de beslissingsfouten zijn er dan slechts twee mogelijkheden (zie onderste rij van schema): ofwel is de beslissing correct, ofwel hebben we een type I fout gemaakt. Over de type I fout weten we echter dat ze slechts voorkomt met een kleine kans. Anderzijds, indien \(p\geq \alpha\) en we \(H_0\) niet verwerpen, dan zijn er ook twee mogelijkheden: ofwel is de beslissing correct, ofwel hebben we een type II fout gemaakt. De kans op een type II fout (\(\beta\)) is echter niet gecontroleerd op een gespecifieerde waarde. De statistische test is zodanig geconstrueerd dat ze enkel de kans op een type I fout controleert (op \(\alpha\)). Om wetenschappelijk eerlijk te zijn, moeten we een pessimistische houding aannemen en er rekening mee houden dat \(\beta\) groot zou kunnen zijn (i.e. een kleine kracht).
Bij \(p < \alpha\) wordt de nulhypothese verworpen en we mogen hieruit concluderen dat \(H_1\) waarschijnlijk juist is. Dit noemen we een sterke conclusie. Bij \(p\geq \alpha\) wordt de nulhypothese aanvaard, maar dat impliceert niet dat we concluderen dat \(H_0\) juist is. We kunnen enkel besluiten dat de data onvoldoende bewijskracht tegen \(H_0\) ten gunste van \(H_1\) bevatten. Dit noemen we een daarom zwakke conclusie.
We illustreren dit opnieuw in een simulatiestudie:
- n=15
- \(\mu=-2\) mmHg, er is dus een bloeddrukdaling van 2 mmHg door de behandeling.
- \(\sigma =9\) mmHg
- 1000 gesimuleerde steekproeven
nsim <- 10000
n <- 15
sigma <- 9
mu <- -2
mu0 <- 0
alpha <- 0.05
#simulate nsim samples of size n
deltaSim <- matrix(
rnorm(n*nsim, mu, sigma),
nrow=n,
ncol=nsim)
pSim <- apply(
deltaSim,
2,
function(x,mu,alternative)
t.test(x,
mu = mu,
alternative = alternative)$p.value,
mu = mu0,
alternative = "less"
)
mean(pSim<alpha)
## [1] 0.2055
pSim %>%
as.data.frame %>%
ggplot(aes(x=.)) +
geom_histogram() +
xlim(0,1)
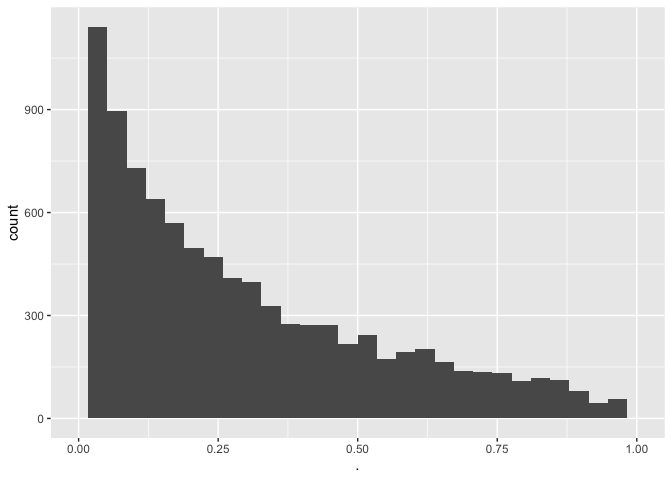
- We observeren dat een power van 0.2055 of een type II error van 0.7945.
Opdracht:
Voer de simulatiestudie opnieuw uit verdubbel hierbij het aantal observaties in de steekproef. Wat observeer je?