Controle van beslissingsfouten

Hoe controleert statistiek de kans op het trekken van foute conclusies?

In onderstaande code trekken we 10000 herhaalde steekproeven van 5 vrouwen en 5 mannen uit de NHANES studie.

Code

Deze code is vrij complex. Het kan nuttig zijn om deze pas na de twee modules Introductie tot R, en, data visualisatie opnieuw te bekijken.

set.seed(15152)
# Aantal simulaties en steekproefgrootte per groep
nSim <- 10000
nSamp <- 5

# We filteren de data vooraf zodat we dit niet telkens opnieuw hoeven te doen
fem <- nhanesSub %>%
  filter(Gender == "female")

mal <- nhanesSub %>%
  filter(Gender == "male")

# Simulatie studie
# Om snelle functies te kunnen gebruiken nemen we eerst nSim steekproeven en berekenen we daarna alles.

femSamps <- malSamps <-matrix(NA, nrow=nSamp, ncol=nSim)
for (i in 1:nSim)
{
  femSamps[,i] <- sample(fem$Height, nSamp)
  malSamps[,i] <- sample(mal$Height, nSamp)
}

res <- data.frame(
  verschil=colMeans(femSamps) - colMeans(malSamps),
  Rfast::ttests(femSamps, malSamps)
  )

sum(res$pvalue < 0.05 & res$verschil < 0)

## [1] 7234

sum(res$pvalue >= 0.05)

## [1] 2766

sum(res$pvalue < 0.05 & res$verschil>0)

## [1] 0

res %>%
  ggplot(aes(x=verschil,y=-log10(pvalue),color=pvalue < 0.05)) +
  geom_point() +
  xlab("Gemiddeld Verschil (cm)") +
  ylab("Statistische Significantie (-log10 p)")

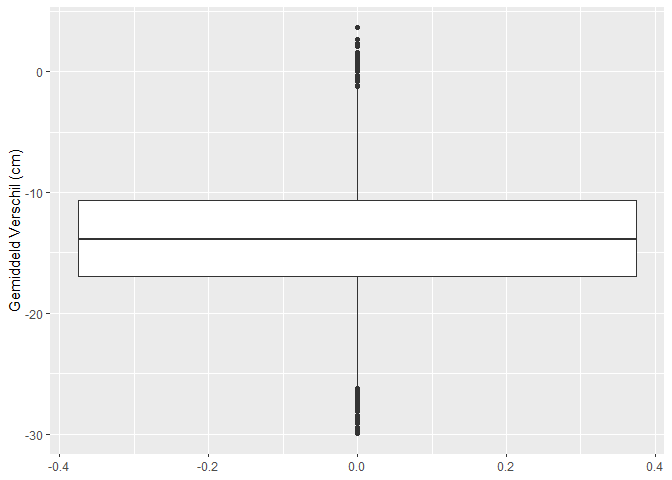
res %>%
  ggplot(aes(y = verschil)) +
  geom_boxplot() +
  ylab("Gemiddeld Verschil (cm)")

  xlab("")

## $x
## [1] ""
## 
## attr(,"class")
## [1] "labels"

Op basis van 10000 steekproeven van 5 mannen en 5 vrouwen zagen we dat in 7234 steekproeven vrouwen gemiddeld significant kleiner zijn dan mannen. In 2766 steekproeven besluiten we dat vrouwen en mannen gemiddeld niet significant verschillen in lengte. En in 0 besluiten we dat vrouwen gemiddeld significant groter zijn dan mannen.

De steekproef die we toonden waaruit we zouden besluiten dat vrouwen significant groter zijn dan mannen is heel onwaarschijnlijk. Er moesten 88605 steekproeven worden getrokken om deze extreme steekproef te vinden.
Het feit dat we in veel steekproeven resultaten vinden die statistisch niet significant zijn komt omdat de statistische toets een te lage kracht heeft om het verschil te detecteren wanneer er maar 5 observaties zijn per groep.

Grotere steekproef?

Wat gebeurt er als we de steekproef verhogen naar 50 observaties per groep?

set.seed(11145)
# Aantal simulaties en steekproefgrootte per groep
nSim <- 10000
nSamp <- 50

# We filteren de data vooraf zodat we dit niet telkens opnieuw hoeven te doen
fem <- nhanesSub %>%
  filter(Gender == "female")

mal <- nhanesSub %>%
  filter(Gender == "male")

# Simulatie studie
# Om snelle functies te kunnen gebruiken nemen we eerst nSim steekproeven en berekenen we daarna alles.

femSamps <- malSamps <- matrix(NA, nrow = nSamp, ncol = nSim)
for (i in 1:nSim)
{
  femSamps[,i] <- sample(fem$Height, nSamp)
  malSamps[,i] <- sample(mal$Height, nSamp)
}

res <- data.frame(
  verschil = colMeans(femSamps) - colMeans(malSamps),
  Rfast::ttests(femSamps, malSamps)
  )

sum(res$pvalue < 0.05 & res$verschil < 0)

## [1] 10000

sum(res$pvalue >= 0.05)

## [1] 0

sum(res$pvalue < 0.05 & res$verschil > 0)

## [1] 0

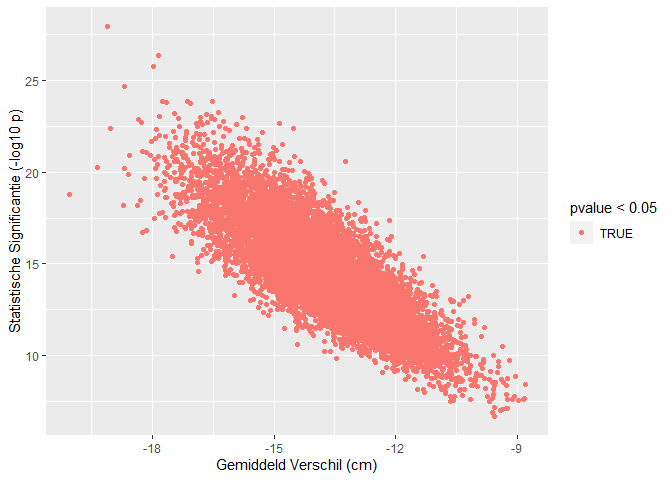
res %>%
  ggplot(aes(x=verschil,y=-log10(pvalue),color=pvalue<0.05)) +
  geom_point() +
  xlab("Gemiddeld Verschil (cm)") +
  ylab("Statistische Significantie (-log10 p)")

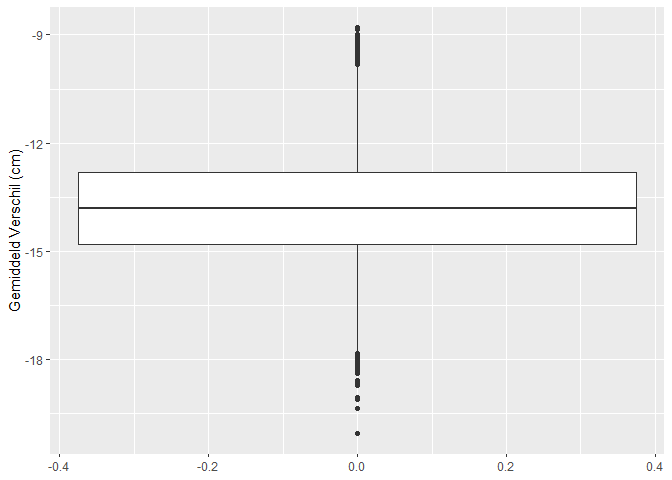
res %>%
  ggplot(aes(y=verschil)) +
  geom_boxplot() +
  ylab("Gemiddeld Verschil (cm)")

  xlab("")

## $x
## [1] ""
## 
## attr(,"class")
## [1] "labels"

We zien dus dat we de kans om een verschil te vinden als er in werkelijkheid een verschil is in de populatie kunnen beïnvloeden in de design fase: aan de hand van de steekproefgrootte.
Hoe meer gegevens hoe makkelijker we het werkelijk verschil oppikken in de steekproef.
Dat wordt ook geïllustreerd in het gemiddelde verschil in lengte tussen mannen en vrouwen: daar zit in de grote studie veel minder variabiliteit op van steekproef tot steekproef omdat ze veel nauwkeuriger kunnen worden geschat omdat er meer gegevens zijn in de steekproef.

Controle van vals positieven

Wat gebeurt er als er geen verschil is tussen beide groepen?

We moeten hiervoor experimenten simuleren waarbij de groepen gelijk zijn.
Hiervoor zullen we twee groepen vergelijken waarvoor de lengte gemiddeld niet verschillend is.
Dat kunnen we doen door een steekproef te trekken waarbij we voor beide groepen at random subjecten trekken uit de subset van vrouwen in de NHANES studie. Dan weten we dat er on de populatie geen verschil is in lengte tussen beide groepen die we zullen vergelijken.
Als we toch een verschil vinden in een steekproef dan weten we dat dit een vals positief resultaat is!
We doen de simulatiestudie opnieuw voor steekproeven met 5 subjecten per groep

set.seed(13245)
# Aantal simulaties en steekproefgrootte per groep
nSim <- 10000
nSamp <- 5

# We filteren de data vooraf zodat we dit niet telkens opnieuw hoeven te doen
fem <- nhanesSub %>%
  filter(Gender == "female")

# Simulatie studie
# Om snelle functies te kunnen gebruiken nemen we eerst nSim steekproeven en berekenen we daarna alles.

femSamps <- femSamps2 <-matrix(NA, nrow=nSamp, ncol=nSim)
for (i in 1:nSim)
{
  femSamps[,i] <- sample(fem$Height, nSamp)
  femSamps2[,i] <- sample(fem$Height, nSamp)
}

res <- data.frame(
  verschil=colMeans(femSamps) - colMeans(femSamps2),
  Rfast::ttests(femSamps, femSamps2)
  )

sum(res$pvalue < 0.05 & res$verschil < 0)

## [1] 213

sum(res$pvalue >= 0.05)

## [1] 9558

sum(res$pvalue < 0.05 & res$verschil>0)

## [1] 229

res %>%
  ggplot(aes(x=verschil,y=-log10(pvalue),color=pvalue < 0.05)) +
  geom_point() +
  xlab("Gemiddeld Verschil (cm)") +
  ylab("Statistische Significantie (-log10 p)")

res %>%
  ggplot(aes(y = verschil)) +
  geom_boxplot() +
  ylab("Gemiddeld Verschil (cm)")

  xlab("")

## $x
## [1] ""
## 
## attr(,"class")
## [1] "labels"

Op basis van 10000 steekproeven zien we dat we in 442 steekproeven ten onrechte besluiten dat er een verschil is in gemiddelde lengte tussen twee groepen vrouwen.

Met de statistische analyse controleren we dus het aantal vals positieve resultaten correct op 5%.

Wat gebeurt er als we het aantal observaties verhogen?

We simuleren opnieuw experimenten met 50 subjecten per groep maar we trekken de subjecten opnieuw telkens uit de populatie van vrouwen.

set.seed(1345)
# Aantal simulaties en steekproefgrootte per groep
nSim <- 10000
nSamp <- 50

# We filteren de data vooraf zodat we dit niet telkens opnieuw hoeven te doen
fem <- nhanesSub %>%
  filter(Gender == "female")

# Simulatie studie
# Om snelle functies te kunnen gebruiken nemen we eerst nSim steekproeven en berekenen we daarna alles.

femSamps <- femSamps2 <-matrix(NA, nrow=nSamp, ncol=nSim)
for (i in 1:nSim)
{
  femSamps[,i] <- sample(fem$Height, nSamp)
  femSamps2[,i] <- sample(fem$Height, nSamp)
}

res <- data.frame(
  verschil=colMeans(femSamps) - colMeans(femSamps2),
  Rfast::ttests(femSamps, femSamps2)
  )

sum(res$pvalue < 0.05 & res$verschil < 0)

## [1] 271

sum(res$pvalue >= 0.05)

## [1] 9501

sum(res$pvalue < 0.05 & res$verschil>0)

## [1] 228

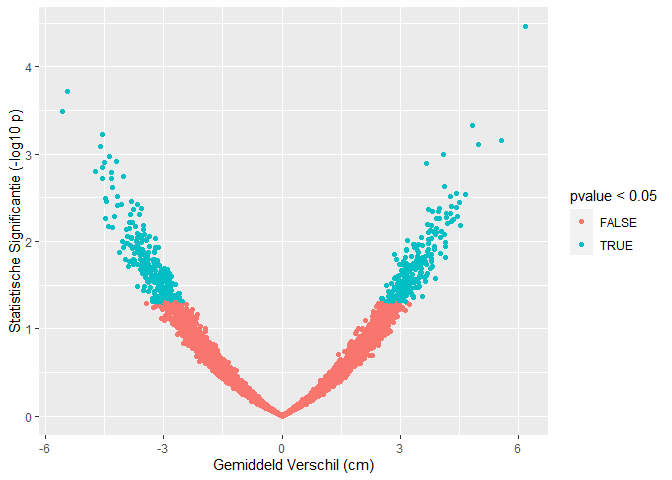
res %>%
  ggplot(aes(x=verschil,y=-log10(pvalue),color=pvalue < 0.05)) +
  geom_point() +
  xlab("Gemiddeld Verschil (cm)") +
  ylab("Statistische Significantie (-log10 p)")

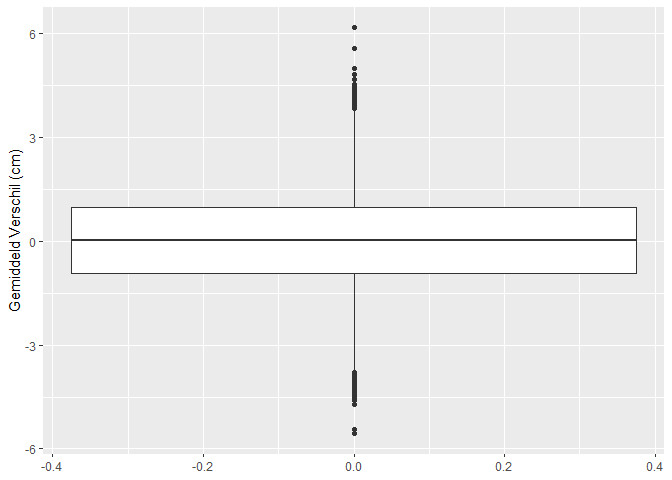
res %>%
  ggplot(aes(y = verschil)) +
  geom_boxplot() +
  ylab("Gemiddeld Verschil (cm)")

  xlab("")

## $x
## [1] ""
## 
## attr(,"class")
## [1] "labels"

Op basis van 10000 steekproeven zien we dat we in 499 steekproeven ten onrechte besluiten dat er een verschil is in gemiddelde lengte tussen twee groepen vrouwen.

Met de statistische analyse controleren we dus ook bij het nemen van een grote steekproef het aantal vals positieve resultaten correct op 5%. (Vals positief: Op basis van de steekproef besluiten dat er gemiddeld een verschil is in lengte tussen beide groepen terwijl er in werkelijkheid geen verschil is in de populatie.)