De normale conforme projectie of mercatorprojectie is een kaartprojectie — vernoemd naar de Vlaamse cartograaf Gerardus Mercator¹ die de projectie in 1569 introduceerde. De projectie is een belangrijk speciaal geval van hoekgetrouwe cilinderprojectie² waarbij de hoeken tussen verschillende richtingen op de kaart gelijk zijn aan de hoeken tussen die richtingen op het aardoppervlak. Hierdoor staan onder andere alle meridianen³ loodrecht op alle parallellen⁴.

Indicatrix van Tissot van de mercatorprojectie. Bij deze projectie is de schaal niet afhankelijk van de richting, wat tot uiting komt in de cirkelvorm van de ellipsen. De schaal is wel afhankelijk van de breedte, wat tot uiting komt in het groter worden van de cirkels op hogere breedte. In afwijking van de theorie van Tissot zijn de cirkels niet infinitesimaal klein vanwege de zichtbaarheid.

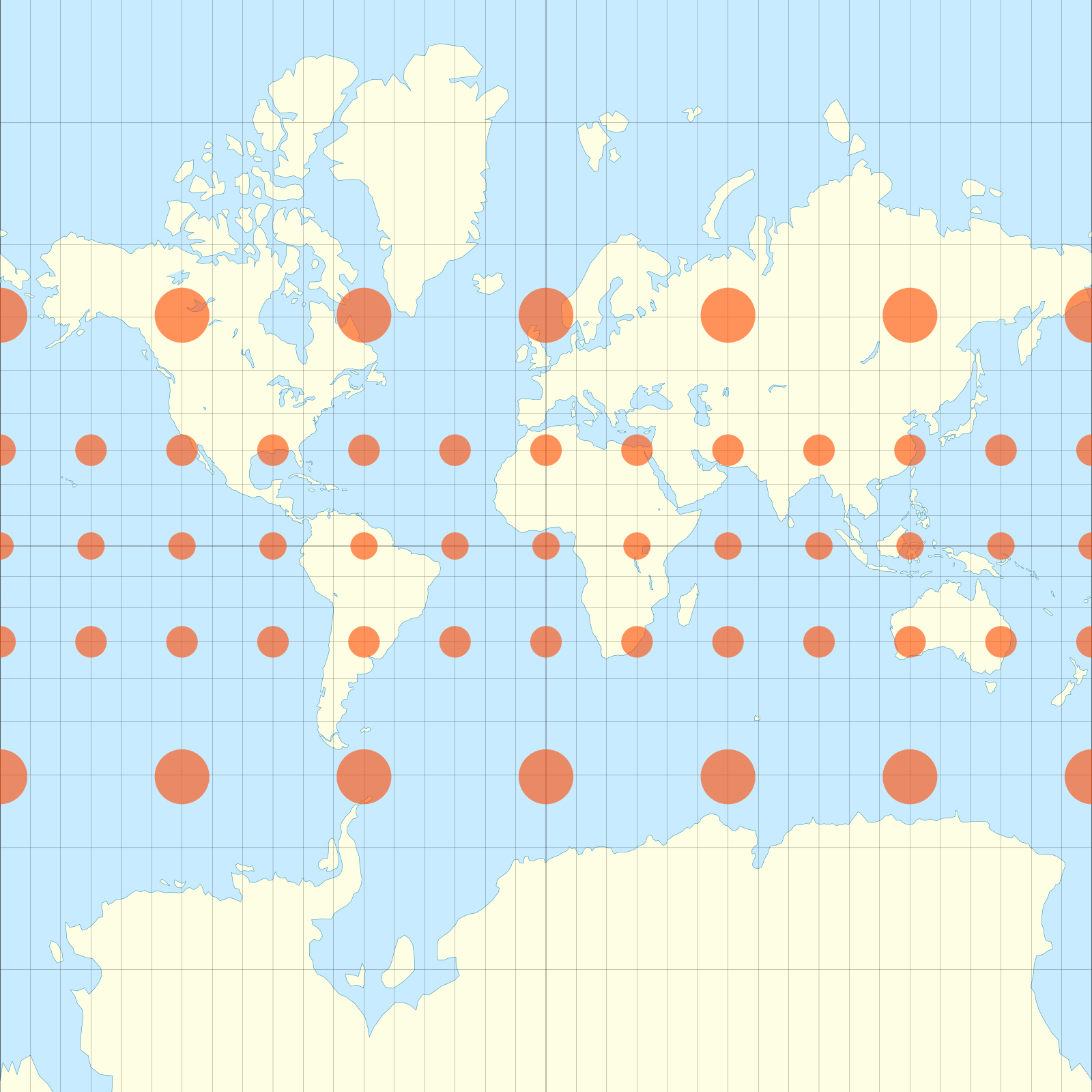
Mercatorprojectie heeft de bijzondere eigenschap dat kompaskoersen getrouw weergegeven worden. Dit is van groot belang voor de scheepvaart omdat lijnen met constante kompaskoers (loxodromen⁵) op een mercatorkaart ook rechte lijnen vormen. Hoewel de projectie daarom veelvuldig gebruikt wordt, wordt ze tegenwoordig minder geschikt geacht voor meer algemeen gebruik van wereldkaarten in atlassen en dergelijke.

Geen enkele projectie kan de Aarde zonder vervormingen weergeven op een plat vlak. Bij mercatorprojectie treden oppervlaktevervormingen op, waarbij gebieden groter worden weergegeven naarmate ze verder van de evenaar liggen. Op de polen is de vergroting zelfs oneindig groot. Bij mercatorprojectie wordt Groenland bijvoorbeeld ongeveer even groot weergegeven als het continent Afrika, terwijl het in werkelijkheid zo'n 17 maal kleiner is. Politici maakten daar tijdens de Koude Oorlog dankbaar gebruik van: de Sovjet-Unie leek door zijn noordelijke ligging immers nog groter en vormde daardoor als het ware een grotere bedreiging voor Europa. Een ander nadeel is dat de kortste route tussen twee punten — de orthodroom⁶ — bij deze kaartprojectie geen rechte lijn is. De kortste route van Amsterdam naar San Francisco lijkt op een mercatorprojectie over Engeland, de Atlantische Oceaan en de continentale VS te lopen. In werkelijkheid vliegen vliegtuigen vrijwel over de Noordpool en Canada.

Een punt op Aarde met lengtegraad $$\lambda$$ en breedtegraad $$\varphi$$ wordt bij mercatorprojectie als volgt omgezet naar een $$(x, y)$$-coördinaat op een rechthoek met afmetingen $$360 \times 180$$: \[ \begin{align} x &= (\lambda - \lambda_0 + 180)\!\!\!\!\mod{360} - 180 \\ \\ y &= 15 \cdot \ln\left(\frac{1 + \sin(\varphi)}{1 - \sin(\varphi)}\right) \end{align} \] Hierbij correspondeert het middelpunt van de rechthoek (met coördinaat $$(0,0)$$) met het punt op Aarde met lengtegraad $$\lambda_0$$ en breedtegraad 0. De rest na deling van $$x$$ door 360 wordt voorgesteld als $$x\!\!\!\!\mod{360}$$ en de functie $$\ln$$ stelt de natuurlijke logaritme voor.

Invoer

Drie getallen $$\lambda_0, \lambda, \varphi \in \mathbb{R}$$ die hoeken (in graden) voorstellen. Elk getal staat op een afzonderlijke regel.

Uitvoer

De mercatorprojectie $$(x, y)$$ van een punt op Aarde met lengtegraad $$\lambda$$ en breedtegraad $$\varphi$$ op een rechthoek met afmetingen $$360 \times 180$$. Het middelpunt van de rechthoek (met coördinaat $$(0,0)$$) correspondeert met lengtegraad $$\lambda_0$$ en breedtegraad 0.

De $$x$$- en $$y$$-coördinaat worden uitgeschreven op afzonderlijke regels, voorafgegaan door de letter x (resp. de letter y), een dubbelpunt (:) en een spatie.

Voorbeeld

Invoer:

0.0
10.0
45.0

Uitvoer:

x: 10.0
y: 26.441207610586293