Nim is een strategisch spelletje voor twee spelers. De speler die als eerste aan de beurt is, mag bepalen hoeveel stapels lucifers ($$n \geq 2$$) er gemaakt worden en hoeveel lucifers er in elke stapel liggen. Het aantal lucifers mag verschillen per stapel en stapels mogen ook leeg zijn. Om naar de stapels te kunnen verwijzen, worden ze oplopend genummerd van 1 tot en met $$n$$. Hieronder zie je bijvoorbeeld een startconfiguratie met vijf stapels, waarvan de vierde leeg is.

Mogelijke startconfiguratie van het spelletje Nim.

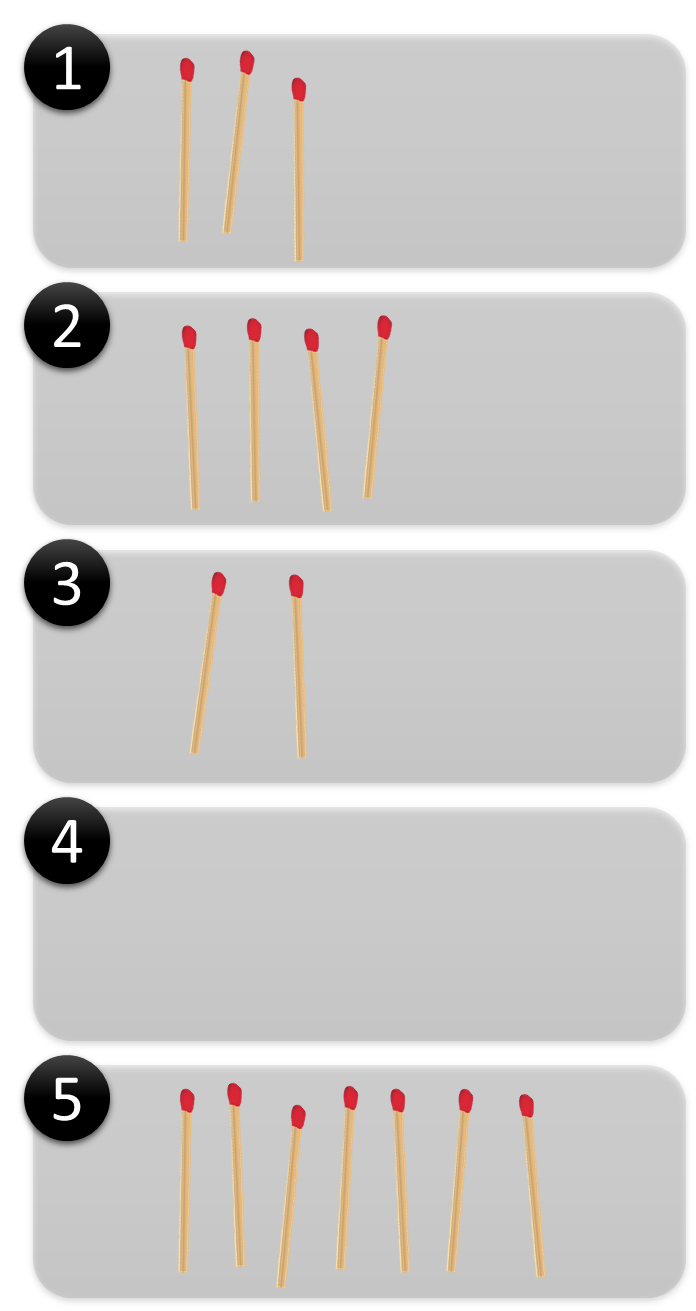
Daarna doen de spelers om de beurt een zet, die erin bestaat dat ze minimaal één en maximaal alle lucifers van één stapel wegnemen. De speler die de laatste lucifer wegneemt, wint het spel.

Opgave

Definieer een klasse Nim die toelaat om het verloop van een spelletje Nim te simuleren. Bij het aanmaken van een nieuw spelletje (Nim) moeten er twee of meer natuurlijke getallen (int) doorgegeven worden. Deze getallen beschrijven de startconfiguratie van een spelletje: het aantal getallen correspondeert met het aantal stapels en de getallen zelf geven aan hoeveel lucifers er bij aanvang van het spelletje in elke stapel liggen. Als er niet twee of meer natuurlijke getallen aan de initalisatiemethode doorgegeven worden, dan moet er een AssertionError opgeworpen worden met de boodschap ongeldige stapels.

Als er een spelletje $$s$$ (Nim) wordt doorgegeven aan de ingebouwde functie repr, dan moet die een stringvoorstelling (str) teruggeven die leest als een Python expressie om een nieuw spelletje (Nim) aan te maken met een startconfiguratie die correspondeert met het huidige aantal lucifers per stapel in $$s$$. Bekijk onderstaand voorbeeld om te zien hoe deze stringvoorstelling er precies moet uitzien.

Als er een spelletje $$s$$ (Nim) wordt doorgegeven aan de ingebouwde functie str, dan moet die een overzicht (str) teruggeven van het huidige aantal lucifers per stapel. Daarbij worden de stapels van $$s$$ in oplopende volgorde opgelijst, elk op een afzonderlijke regel. Elke stapel wordt voorgesteld door het nummer van de stapel, een dubbelpunt (:), een spatie en evenveel verticale strepen (|) als er lucifers in de stapel liggen. Bekijk onderstaand voorbeeld om te zien hoe dit overzicht er precies moet uitzien.

Voorts moet je op een spelletje $$s$$ (Nim) minstens de volgende methoden kunnen aanroepen:

Een methode wegnemen waaraan twee getallen $$i, j \in \mathbb{N}$$ (int) moeten doorgegeven worden. Als het niet mogelijk is om $$j$$ lucifers weg te nemen uit stapel $$i$$ omdat i) de stapel niet bestaat of ii) er niet minstens één en maximaal alle lucifers uit die stapel weggenomen worden, dan moet er een AssertionError opgeworpen worden met de boodschap ongeldige zet en mag de methode ook geen lucifers wegnemen. Anders moet de methode $$j$$ lucifers wegnemen uit stapel $$i$$ en een referentie naar spelletje $$s$$ teruggeven.
Een methode isafgelopen waaraan geen argumenten moeten doorgegeven worden. De methode moet een Booleaanse waarde (bool) teruggeven, die aangeeft of spelletje $$s$$ afgelopen is. Dat is het geval als er geen enkele lucifer meer overblijft.

Zorg dat voor twee spelletjes $$s$$ (Nim) en $$s'$$ (Nim) de bewerking $$s + s'$$ resulteert in een nieuw spelletje $$s''$$ (Nim) met evenveel stapels als het maximum aantal stapels van $$s$$ en $$s'$$. Het aantal lucifers in elke stapel van $$s''$$ moet gelijk zijn aan de som van het aantal lucifers in de overeenkomstige stapels van $$s$$ en $$s'$$, waarbij onbestaande stapels per definitie geen lucifers bevatten. De bewerking mag de spelletjes $$s$$ en $$s'$$ niet wijzigen.

Voorbeeld

        >>> nim = Nim(3, 4, 2, 0, 7)
>>> nim
Nim(3, 4, 2, 0, 7)
>>> print(nim)
1: |||
2: ||||
3: ||
4:
5: |||||||
>>> nim.wegnemen(2, 3)
Nim(3, 1, 2, 0, 7)
>>> print(nim)
1: |||
2: |
3: ||
4:
5: |||||||
>>> nim.wegnemen(5, 2).wegnemen(5, 1)
Nim(3, 1, 2, 0, 4)
>>> nim.wegnemen(1, 4)            # te weinig lucifers in stapel
Traceback (most recent call last):
AssertionError: ongeldige zet
>>> nim.wegnemen(7, 1)            # onbestaande stapel
Traceback (most recent call last):
AssertionError: ongeldige zet
>>> nim.wegnemen(3, 0)            # er moet minstens één lucifer weggenomen worden
Traceback (most recent call last):
AssertionError: ongeldige zet
>>> print(nim)
1: |||
2: |
3: ||
4:
5: ||||
>>> nim.isafgelopen()
False
>>> nim.wegnemen(1, 3).wegnemen(2, 1).wegnemen(3, 2).wegnemen(5, 4)
Nim(0, 0, 0, 0, 0)
>>> nim.isafgelopen()
True

>>> Nim(4, 3, 0, 5) + Nim(3, 0, 2, 1, 6, 2)
Nim(7, 3, 2, 6, 6, 2)

>>> Nim(1.0, 2.0, 3.0, 4.0, 5.0)     # alle argumenten moeten integers zijn
Traceback (most recent call last):
AssertionError: ongeldige stapels
>>> Nim('drie', 'zeven', 'twee')     # alle argumenten moeten integers zijn
Traceback (most recent call last):
AssertionError: ongeldige stapels
>>> Nim(7)                           # er moeten minstens twee argumenten zijn
Traceback (most recent call last):
AssertionError: ongeldige stapels