Beschouw een populatie bacteriën, elk met een plasmide van een welbepaald type: $$m$$ met een plasmide van type I, $$n$$ met een plasmide van type II en $$k$$ met een plasmide van type III. Telkens wanneer twee bacteriën met een verschillend type plasmide elkaar ontmoeten, muteert hun plasmide naar dat van het overblijvende type. Wanneer bijvoorbeeld een type I bacterie en een type III bacterie elkaar ontmoeten, dan muteert het plasmide van beide bacteriën naar type II. We willen nu de evolutie van een gegeven populatie bacteriën doorheen de tijd simuleren.

Opgave

Ontwikkel een klasse Populatie waarvan elk object een populatie van bacteriën voorstelt. Elk met een plasmide van een welbepaald type. Alle objecten van deze klasse moeten een attribuut populatie hebben: een lijst van getallen met waarde 1, 2 of 3, waarbij elk element van de lijst een bacterie uit de populatie voorstelt en de bijhorende waarde aangeeft welk type plasmide die bacterie heeft (op een bepaald tijdstip). Voorts moeten alle objecten ook een attribuut ontmoetingen hebben, waarin wordt bijgehouden hoeveel ontmoetingen tussen bacteriën er reeds hebben plaatsgevonden. De klasse Populatie moet daarnaast ook ondersteuning bieden aan de volgende methoden:

De initialisatiemethode __init__ moet ervoor zorgen dat het attribuut populatie een initiële populatie voorstelt met $$m$$ bacteriën met een plasmide van type I, $$n$$ met een plasmide van type II en $$k$$ met een plasmide van type III. De waarden $$m$$, $$n$$ en $$k$$ zijn optionele argumenten van de methode __init__ met standaardwaarde 0. Nadat deze methode is uitgevoerd, moet het attribuut ontmoetingen van het nieuw aangemaakte object de waarde nul hebben, en moeten het attribuut populatie een waarde hebben zoals hieronder schematisch wordt weergegeven.
De methode plasmiden moet als resultaat een tuple ($$m$$, $$n$$, $$k$$) teruggeven, waarbij de waarden $$m$$, $$n$$ en $$k$$ het aantal bacteriën in de populatie met plasmiden van resp. type I, type II en type III aangeven.
De methode __str__ moet als resultaat een string teruggeven van de vorm "type I: m, type II: n, type III: k (na x ontmoetingen)", waarbij de waarden $$m$$, $$n$$, $$k$$ en $$x$$ moeten ingevuld worden overeenkomstig de huidige toestand van het object.
De methode __repr__ moet als resultaat een string teruggeven van de vorm "Populatie(m, n, k)", waarbij de waarden $$m$$, $$n$$ en $$k$$ moeten ingevuld worden overeenkomstig de huidige toestand van het object.
De methode grootte moet als resultaat de grootte van de populatie (het totaal aantal bacteriën) teruggeven.
De methode ontmoeting moet een ontmoeting tussen twee bacteriën uit de populatie simuleren, zoals in de inleiding werd beschreven. Aan deze methode moeten twee parameters $$0 \leq i,j < m+n+k$$ doorgegeven worden. Als de bacteriën $$i$$ en $$j$$ uit de populatie een verschillende type plasmide hebben, dan moet het plasmide van beide bacteriën muteren naar het derde type. Dit wordt schematisch voorgesteld in onderstaande afbeelding.

Zorg er bij je implementatie van de klasse Populatie voor dat de verschillende methoden optimaal hergebruikt worden. Onderstaande interactieve Python sessie illustreert het gebruik van de klasse Populatie.

>>> populatie = Populatie(m=998, n=1, k=1)
>>> print(populatie)
type I: 998, type II: 1, type III: 1 (na 0 ontmoetingen)
>>> print(repr(populatie))
Populatie(998, 1, 1)
>>> print(populatie.plasmiden())
(998, 1, 1)
>>> for i in range(populatie.grootte()-1):
...   populatie.ontmoeting(i, i+1)
>>> print(populatie)
type I: 997, type II: 0, type III: 3 (na 999 ontmoetingen)
>>> for i in range(populatie.grootte()-1):
...   populatie.ontmoeting(i, i+1)
>>> print(populatie)
type I: 997, type II: 3, type III: 0 (na 1998 ontmoetingen)

Schrijf daarenboven nu ook nog een functie

simulatie(populatie[, aantal][, weergave])

waaraan als verplicht argument populatie een object van de klasse Populatie moet doorgegeven worden. Deze functie moet een gegeven aantal ontmoetingen simuleren (optioneel argument aantal met standaarwaarde 1), waarbij de twee bacteriën die elkaar ontmoeten telkens willekeurig in de gegeven populatie moeten gekozen worden. Om de evolutie van de populatie doorheen deze ontmoetingen te kunnen opvolgen, moet de functie zowel de initiële toestand van de populatie als de toestand van de populatie om de zoveel ontmoetingen (gegeven door het optioneel argument weergave met standaardwaarde 1) uitschrijven. Het uitschrijven van de toestand van de populatie moet gebeuren conform het formaat van de methode __str__ van de klasse Populatie. Op die manier genereert de programmacode

populatie = Populatie(m=998, n=1, k=1)
simulatie(populatie, 10000, 250)

bijvoorbeeld de volgende uitvoer (ingekort)

type I: 998, type II: 1, type III: 1 (na 0 ontmoetingen)
type I: 998, type II: 1, type III: 1 (na 250 ontmoetingen)
type I: 995, type II: 4, type III: 1 (na 500 ontmoetingen)
type I: 990, type II: 8, type III: 2 (na 750 ontmoetingen)
...
type I: 337, type II: 357, type III: 306 (na 9500 ontmoetingen)
type I: 328, type II: 348, type III: 324 (na 9750 ontmoetingen)
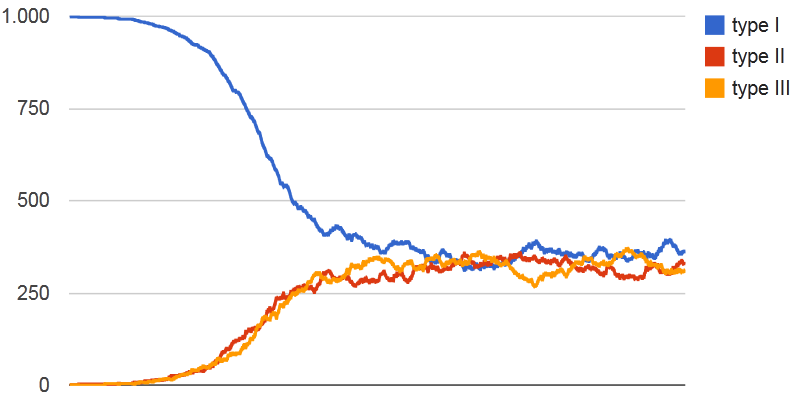
type I: 337, type II: 324, type III: 339 (na 10000 ontmoetingen)

Opmerking: Gezien het niet-deterministisch karakter van de uitvoer van de functie simulatie, wordt de correctheid van je implementatie van deze functie niet beoordeeld door Pythia. In de feedback die door Pythia gegeven wordt, kun je wel zelf nagaan of de evolutie van de populatie die je programmacode genereert, dezelfde trend vertoont als deze in onderstaande figuur.