Een wiskundige constante is een getal waarvan de waarde op een ondubbelzinnige manier wordt vastgelegd door een definitie. De constante wordt vaak aangeduid met een vast symbool (bijvoorbeeld een letter uit een alfabet) of vernoemd naar een wiskundige om het gebruik ervan te vergemakkelijken.
Zo wordt de constante van Archimedes bijvoorbeeld aangeduid door de Griekse letter $$\pi$$ en gedefinieerd als de verhouding tussen de omtrek en de diameter van een cirkel.
Onderstaande tabel bevat de decimale voorstelling van enkele wiskundige constanten, gesorteerd op jaar van ontdekking.
| naam | symbool | decimale voorstelling | jaar |
|---|---|---|---|
| constante van Archimedes | $$\pi$$ | 3.14159265358979323846 | 1900–1600 v.Chr. |
| gulden snede | $$\phi$$ | 1.61803398874989484820 | ~300 v.Chr. |
| constante van Champernowne | $$\text{C}_{10}$$ | 0.12345678910111213141 | 1933 |
| constante van Feigenbaum | $$\delta$$ | 4.66920160910299067185 | 1975 |
Opgave
De piramidale voorstelling van een wiskundige constante $$\alpha$$ bestaat uit $$n \in \mathbb{N}_0$$ verdiepingen, die van boven naar onder genummerd worden vanaf 1. Op de $$i$$-de verdieping ($$i = 1, 2, \ldots, n$$) staan $$i$$ getallen, die telkens de som zijn van de volgende $$i$$ cijfers van $$\alpha$$. Dit zijn bijvoorbeeld de piramidale voorstellingen met 5 verdiepingen van de vier constanten $$\pi$$, $$\phi$$, $$\text{C}_{10}$$ en $$\delta$$.
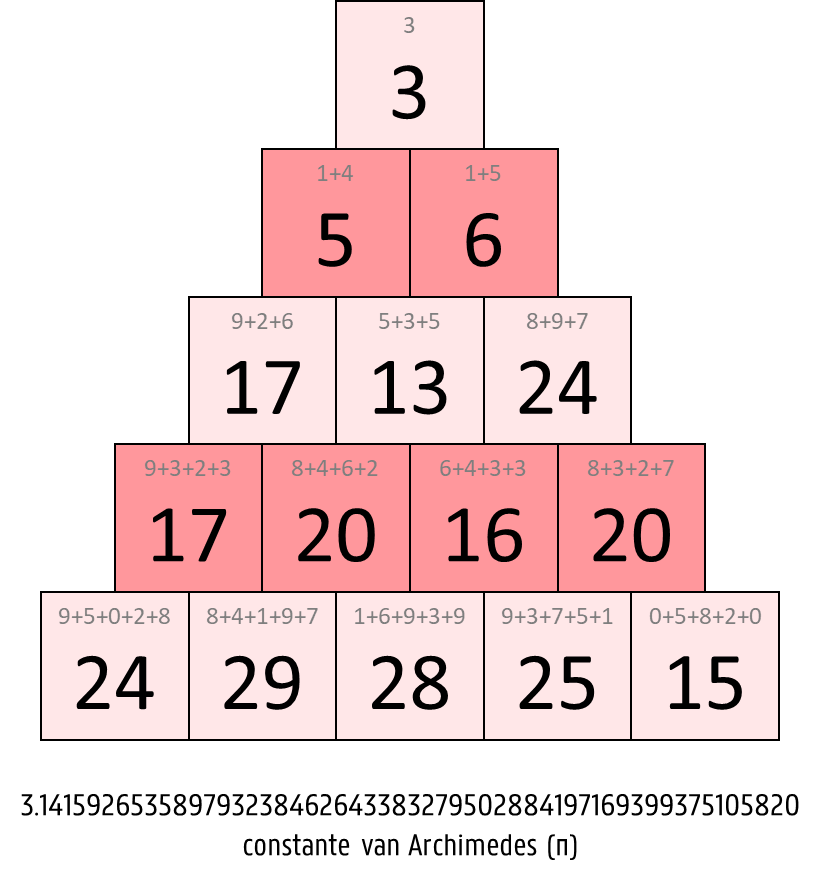
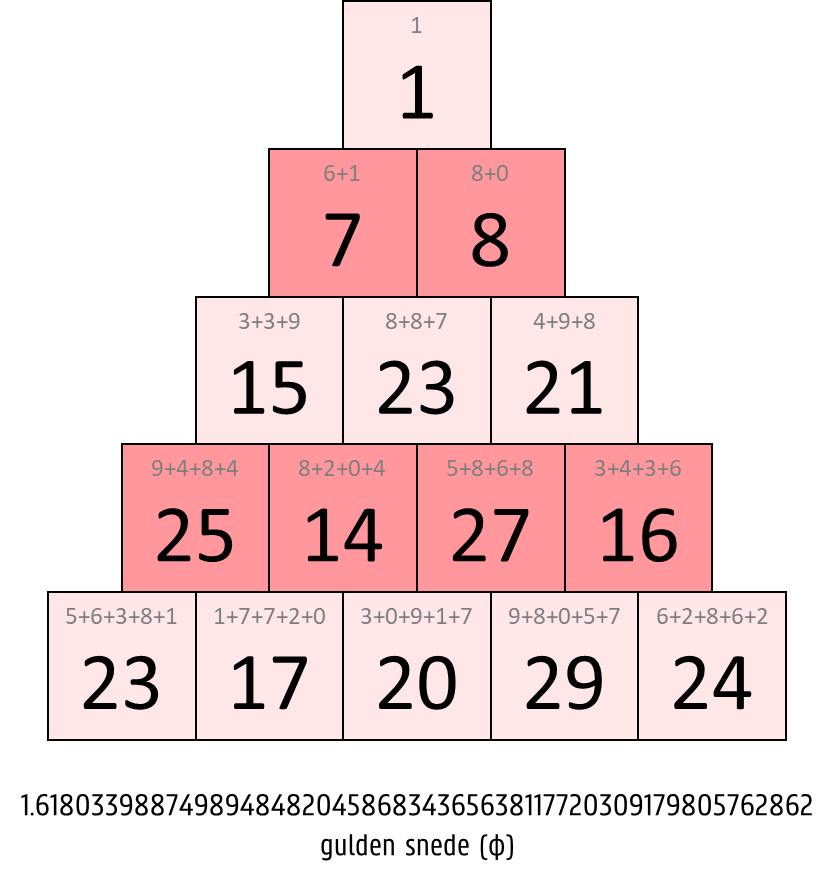
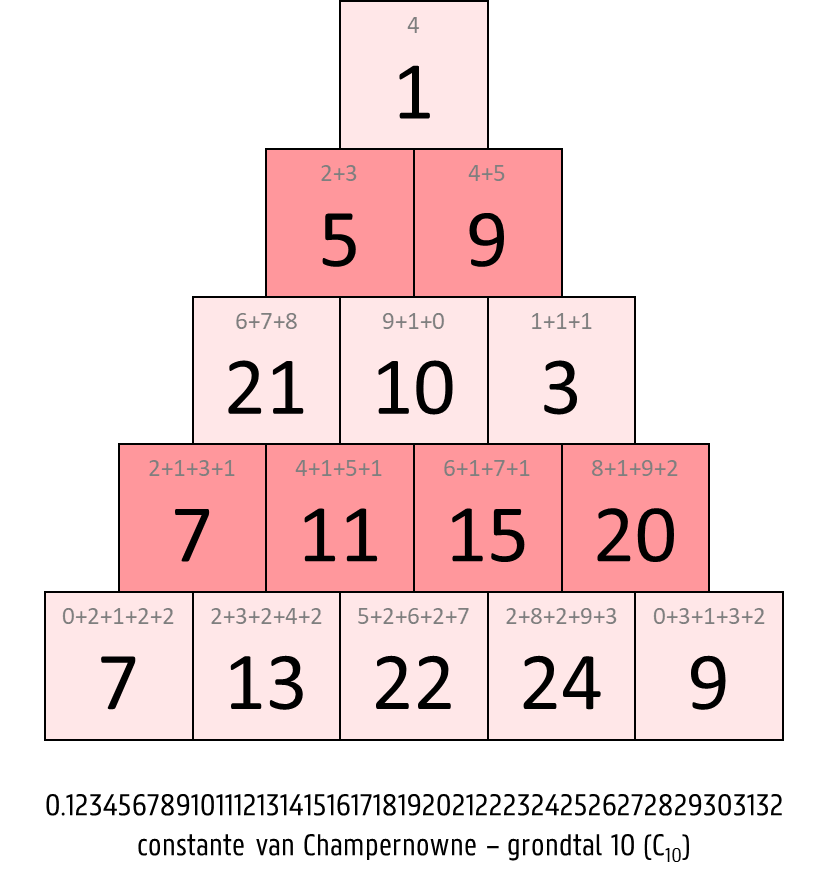
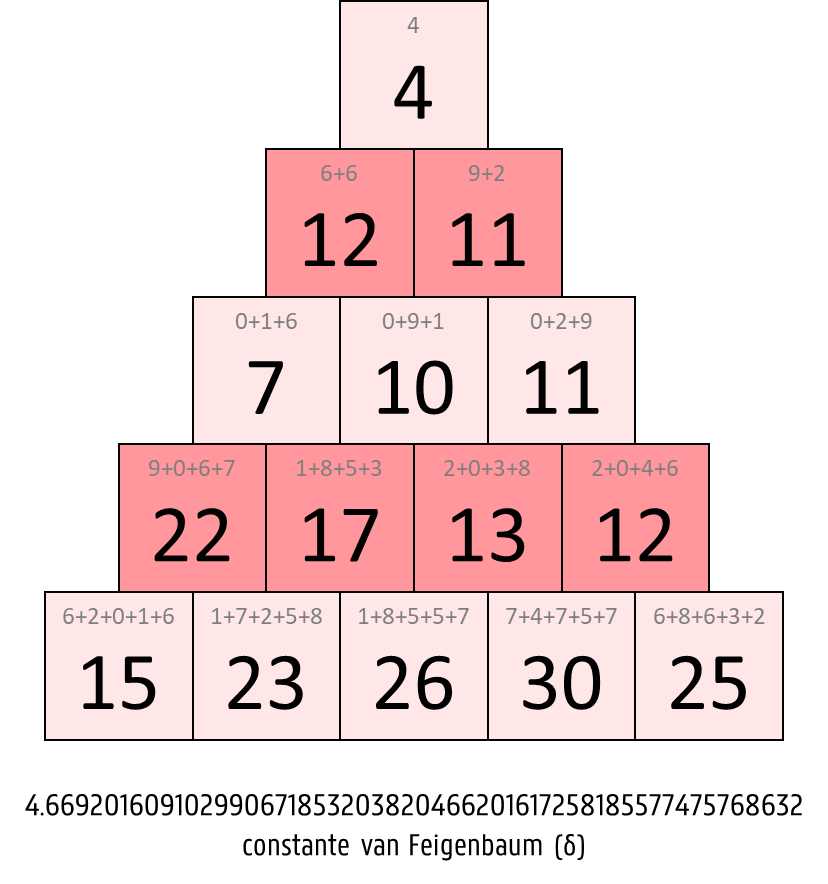
Om de opeenvolgende cijfers van $$\alpha$$ te bepalen, wordt de wiskundige constante eerst op de volgende manier opgekuist. Als $$\alpha$$ een reëel getal is dan verwijderen we het decimale punt. Als $$\alpha$$ negatief is dan verwijderen we het minteken. Van het getal dat we op de manier bekomen, verwijderen we ook alle voorloopnullen. We gebruiken met andere woorden enkel de significante cijfers van $$\alpha$$.
Invoer
De eerste regel bevat de decimale voorstelling van een wiskundige constante $$\alpha$$. De tweede regel bevat een getal $$n \in \mathbb{N}_0$$.
Uitvoer
De piramidale voorstelling van $$\alpha$$ met $$n$$ verdiepingen. Elke verdieping staat op een afzonderlijke regel. De getallen die op dezelfde verdieping staan, worden telkens van elkaar gescheiden door één enkele spatie.
Opmerking
Je mag ervan uitgaan dat er voldoende cijfers van $$\alpha$$ gegeven worden om de piramidale voorstelling met $$n$$ verdiepingen te bepalen.
Voorbeeld ($$\pi$$, constante van Archimedes)
Invoer:
3.141592653589793238462643383279502884197169399375105820
5Uitvoer:
3
5 6
17 13 24
17 20 16 20
24 29 28 25 15Epiloog
NASA1 gebruikt slechts 15 cijfers van $$\pi$$ om interplanetaire reizen te berekenen. Met 40 cijfers kan je de omtrek van een cirkel ter grootte van het zichtbare heelal berekenen, met een foutenmarge die kleiner is dan de diameter van een waterstofatoom.
