Interactie tussen twee continue variabelen
Het zou ook kunnen dat de associatie tussen lpsa en lcavol afhangt van het prostaatgewicht. De gemiddelde toename in lpsa tussen patiënten die één eenheid van log-tumorvolume verschillen zou bijvoorbeeld lager kunnen zijn voor patiënten met een hoog prostaatgewicht dan bij patiënten met een laag prostaatgewicht. Het effect van het tumorvolume op de prostaat antigeen concentratie hangt in dit geval af van het prostaatgewicht.
Om een dergelijke of tussen 2 variabelen \(X_v\) en \(X_w\) statistisch te modelleren, kan men het product van beide variabelen in kwestie aan het model toevoegen:
\[Y_i = \beta_0 + \beta_v x_{iv} + \beta_w x_{iw} +\beta_s x_{is} + \beta_{vw} x_{iv}x_{iw} +\epsilon_i\]Het ‘effect’ van een verschil in 1 eenheid in \(X_v\) op de gemiddelde uitkomst bedraagt nu:
\[\begin{array}{l} E(Y|X_v=x_v+1,X_w=x_w,X_s=x_s) − E(X_v=x_v,X_w=x_w,X_s=x_s) \\ \quad = \beta_0 + \beta_v (x_{v}+1) + \beta_w x_w +\beta_s x_{s} + \beta_{vw} (x_{v}+1) x_w - \beta_0 - \beta_v x_{v} - \beta_w x_w -\beta_s x_{s} - \beta_{vw} (x_{v}) x_w \\ \quad = \beta_v + \beta_{vw} x_w \end{array}\]wanneer het log-prostaatgewicht \(X_w=c\) en de \(X_s=x_s\) status ongewijzigd blijven. Merk op dat het ‘effect’ van een wijzing in het tumorvolume bij constant log-prostaat gewicht nu inderdaad afhankelijk is van de hoogte van het log-prostaatgewicht \(x_w\).
We schatten nu opnieuw de parameters van het model in R.
lmVWS_IntVW <- lm(lpsa~lcavol + lweight + svi + lcavol:lweight ,prostate)
summary(lmVWS_IntVW)
##
## Call:
## lm(formula = lpsa ~ lcavol + lweight + svi + lcavol:lweight,
## data = prostate)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.65886 -0.44673 0.02082 0.50244 1.57457
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.6430 0.7030 -0.915 0.36278
## lcavol 1.0046 0.5427 1.851 0.06734 .
## lweight 0.6146 0.1961 3.134 0.00232 **
## sviinvasion 0.6859 0.2114 3.244 0.00164 **
## lcavol:lweight -0.1246 0.1478 -0.843 0.40156
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7179 on 92 degrees of freedom
## Multiple R-squared: 0.6293, Adjusted R-squared: 0.6132
## F-statistic: 39.05 on 4 and 92 DF, p-value: < 2.2e-16
De output van het model geeft een schatting van -0.125 voor de interactie \(\beta_{vw}\) tussen het log-tumorvolume en het log-prostaatgewicht. Dat betekent dat de gemiddelde toename in lpsa tussen patiënten met een verschil in het log-tumorvolume maar met eenzelfde prostaatgewicht afhankelijk zal zijn van het prostaatgewicht. In het bijzonder suggereert de output dat patiënten die 1% verschillen in het tumorvolume maar hetzelfde log prostaat gewicht hebben gemiddeld (\(1.004-0.125 \times x_w\))% verschillen in prostaat antigeen concentratie (interpretatie volgt uit log transformatie van de response en tumorvolume). Patiënten die 1% verschillen in tumorvolume en die een log-prostaatgewicht hebben van 3 zullen gemiddeld 0.631% in prostaat antigeen concentratie verschillen. Terwijl patiënten die 1% verschillen in tumorvolume en die een log-prostaatgewicht hebben van 4 gemiddeld een verschil van 0.506% in prostaat antigeen concentratie hebben. De associatie van het log-tumorvolume en de log prostaat antigeen concentratie neemt dus af met toenemend prostaatgewicht.
Grafische interpretatie wordt weergegeven in Figuur 64. Hier worden het additieve model en het model met de lcavol:lweight interactie vergeleken. De fit toont duidelijk aan dat de associate tussen lpsa en lcavol gelijk is ongeacht de grootte van het prostaatgewicht voor het additieve model (parallele lijnen in het regressieoppervlak). Voor het model met interactie is dat niet het geval, de associate (helling) neemt af met toenemend prostaatgewicht. We zien een analoog effect wanneer we focussen op de associatie tussen lpsa en lweight. De lpsa \(\leftrightarrow\) lweight associatie neemt af met toenemend log-tumorvolume.
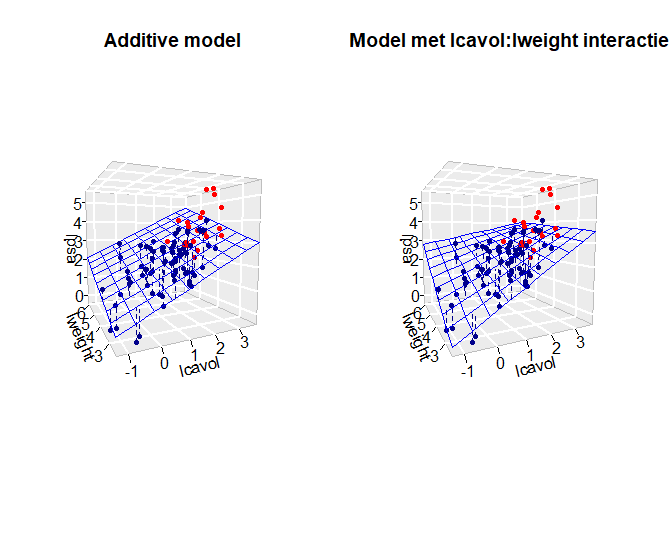
Figuur 64: Fit van het additieve model met de termen lcavol, lweight, svi (links) en het model met interactie lcavol, lweight, svi en lcavol:lweight (rechts). Merk op dat we enkel het regressieoppervlak weergeven voor patiënten zouder invasie van de zaadblaasjes. Dat voor patiënten met invasie van de zaadblaasjes is parallel met het getoonde oppervlak, maar ligt iets hoger. De rechtse figuur toont duidelijk dat de interactie ervoor zorgt dat de associatie tussen de response en het tumorvolume afhankelijk is van de hoogte van het prostaatgewicht en vice versa, dat zorgt voor een torsie in het regressievlak.
Merk op, dat het interactie effect dat geobserveerd wordt in de steekproef echter statistisch niet significant is (p=0.4). Gezien de hoofdeffecten die betrokken zijn in een interactie term niet los van elkaar kunnen worden geïnterpreteerd is de conventie om een interactieterm uit het model te verwijderen wanneer die niet significant is. Na verwijdering van de niet-significante interactieterm kunnen de hoofdeffecten worden geïnterpreteerd.