Welke geheime boodschap zit verborgen in onderstaand rooster?

 Antwoord weergeven

De boodschap is "East, west, home's best.". Voor de ontcijfering ervan wordt een zogenaamde grille gebruikt: een blad papier of een stuk karton met daarop een vierkant $$n \times n$$ rooster waarin enkele openingen uitgeknipt werden. In dit geval een $$5 \times 5$$ rooster waarin zes openingen uitgeknipt worden volgens onderstaand patroon.

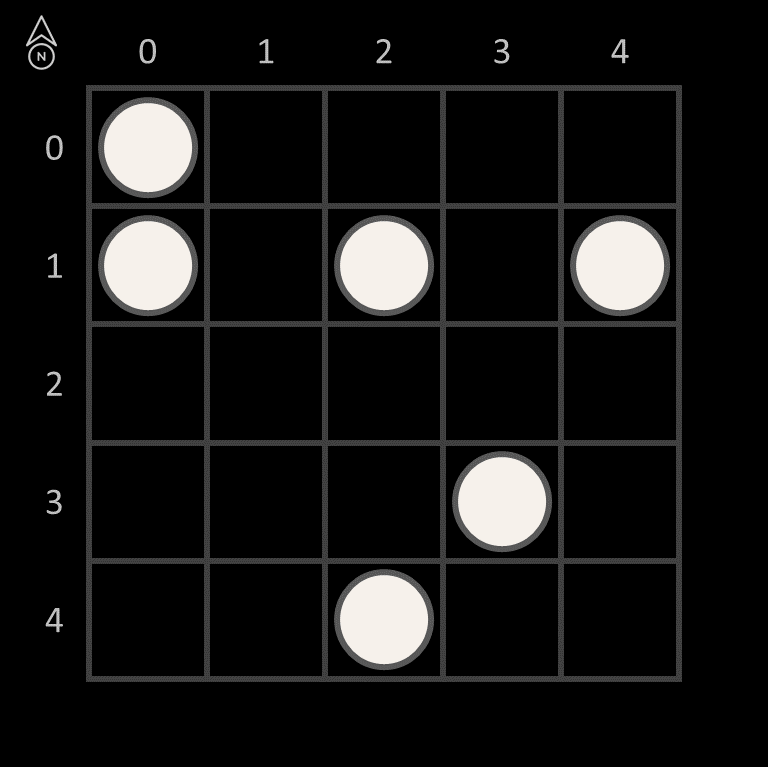
Als de grille op het vierkant rooster gelegd wordt, dan kan doorheen de openingen de tekst "East, " uitgelezen worden (in de leesrichting van links naar rechts, en van boven naar onder). Dit is het eerste deel van de boodschap.

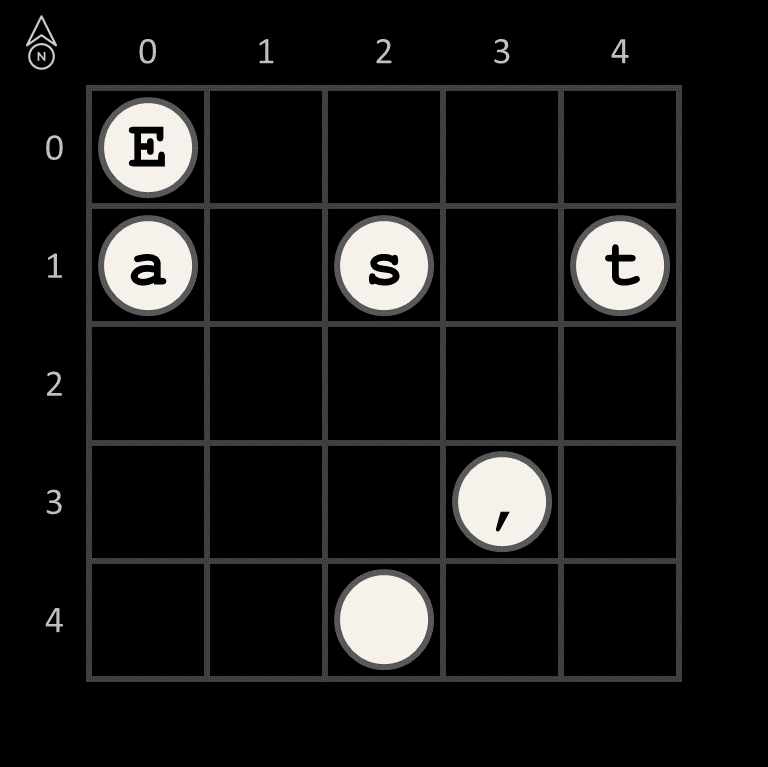
Door de grille 90° in wijzerzin te draaien, kan het tweede deel van de boodschap uitgelezen worden: "West, ". Daarna kan de grille nog tweemaal 90° in wijzerzin gedraaid worden om de twee laatste delen van de boodschap te kunnen uitlezen: "home's" en " best."

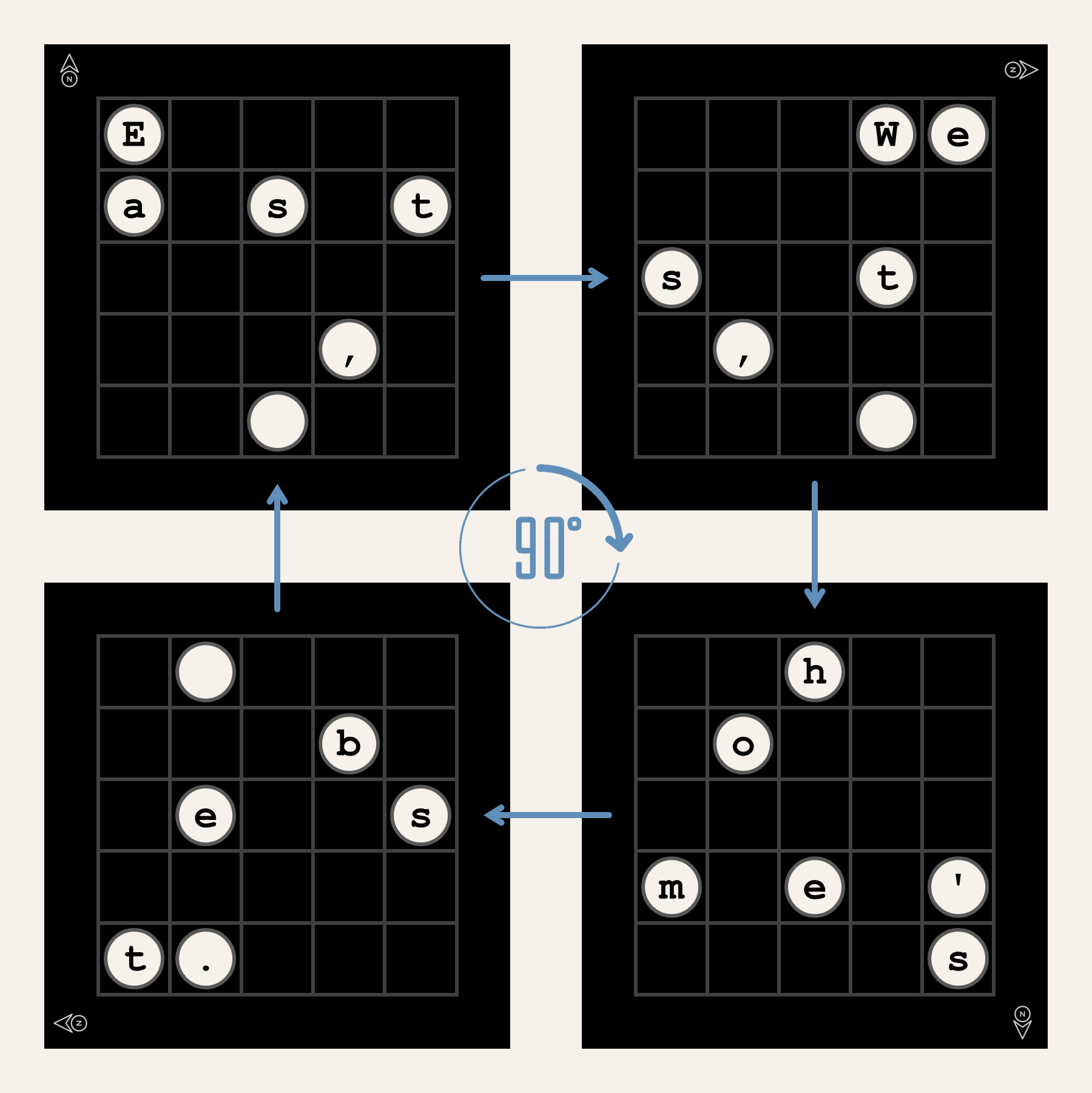
De oudste gekende beschrijving van deze techniek dateert van 1550 en is van de hand van de Italiaanse geleerde Girolamo Cardano¹. Om die reden wordt een grille soms ook een Cardanrooster genoemd.

Opgave

Om te kunnen verwijzen naar de cellen van een rooster (zowel voor een rooster met karakters waarin een geheime boodschap verborgen zit als voor een rooster met de openingen van een grille) worden de rijen van boven naar onder genummerd, en de kolommen van links naar rechts, telkens vanaf nul. Hierdoor kan de positie van een cel voorgesteld worden als een tuple $$(r, k)$$, waarbij $$r \in \mathbb{N}$$ (int) het rijnummer en $$k \in \mathbb{N}$$ (int) het kolomnummer aanduidt.

Een $$n \times n$$ ($$n \in \mathbb{N}_0$$) rooster waarin een geheime boodschap verborgen zit, wordt opgeslaan in een tekstbestand. Daarbij staat elke rij van het rooster op een afzonderlijke regel, en geldt dus dat het bestand uit $$n$$ regels bestaat die elk $$n$$ karakters bevatten. Zo ziet het bestand met het $$5 \times 5$$ rooster waarin de geheime boodschap uit de inleiding verborgen zit er bijvoorbeeld als volgt uit:

E hWe
aosbt
seVts
m,e,'
t.  s

Definieer een klasse Grille om grilles voor te stellen waarmee geheime boodschappen kunnen ontcijferd worden. Bij het aanmaken van een grille (Grille) moeten twee argumenten doorgegeven worden: i) het aantal rijen/kolommen (int) van het vierkant rooster op de grille en ii) een collectie (list, tuple of set) met de posities van de openingen in de grille. Een grille $$g$$ (Grille) moet minstens de volgende eigenschappen hebben:

• dimensie: aantal rijen/kolommen (int) van het vierkant rooster op grille $$g$$

• openingen: verzameling (set) met de posities van de openingen in grille $$g$$

Daarnaast moet je op een grille $$g$$ (Grille) minstens de volgende methoden kunnen aanroepen:

• Een methode decodeer waaraan de locatie (str) moet doorgegeven worden van een tekstbestand met een vierkant rooster waarin een geheime boodschap verborgen zit. De methode moet het deel van de geheime boodschap (str) teruggeven dat kan uitgelezen worden door grille $$g$$ op het rooster te leggen (in de leesrichting van links naar rechts en van boven naar onder).

• Een methode roteer met een optionele parameter wijzerzin waaraan een Booleaanse waarde (bool) kan doorgegeven worden. Op basis van de waarde van de parameter wijzerzin moet de methode ervoor zorgen dat grille $$g$$ 90° in wijzerzin (True, standaardwaarde) of in tegenwijzerzin (False) gedraaid wordt. De methode moet een verwijzing naar grille $$g$$ teruggeven.

  Tip: 90° roteren

  Als een $$n \times n$$ rooster 90° in wijzerzin geroteerd wordt, dan komt een cel met positie $$(r, k)$$ op positie $$(k, n - r - 1)$$ terecht (zie oranje cel in onderstaande figuur).

  

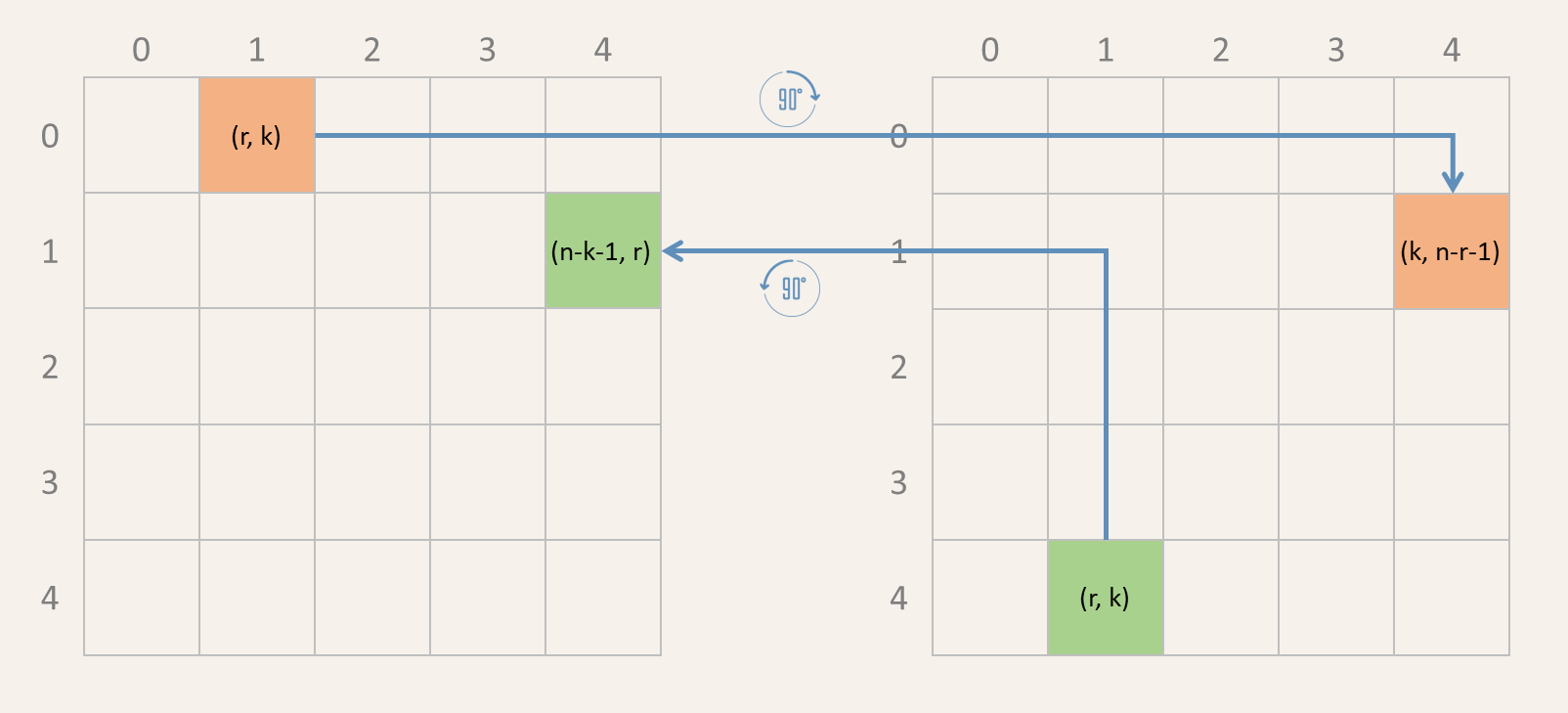
  Als een $$n \times n$$ rooster 90° in tegenwijzerzin geroteerd wordt, dan komt een cel met positie $$(r, k)$$ op positie $$(n - k - 1, r)$$ terecht (zie groene cel in bovenstaande figuur).

Als een grille (Grille) wordt doorgegeven aan de ingebouwde functie str, dan moet een stringvoorstelling (str) van het rooster met openingen teruggegeven worden. Daarin vormt elke rij een afzonderlijke regel, worden cellen met openingen voorgesteld door de hoofdletter O, en worden cellen zonder openingen voorgesteld door een hekje (#).

Twee grilles $$r$$ en $$s$$ (Grille) zijn gelijk (r == s) als ze hetzelfde aantal rijen/kolommen hebben en als ze kunnen gedraaid worden (veelvouden van 90°) zodat ze al hun openingen op dezelfde posities hebben.

Twee grilles $$r$$ en $$s$$ (Grille) optellen (r + s) moet een nieuwe grille $$t$$ (Grille) opleveren die eruit ziet alsof de grilles $$r$$ en $$s$$ bovenop elkaar gelegd worden. Er zitten met andere woorden in $$t$$ enkel openingen op posities waar in beide grilles $$r$$ en $$s$$ openingen zitten. De optelling is enkel gedefinieerd als de grilles $$r$$ en $$s$$ hetzelfde aantal rijen/kolommen hebben. Als dat niet het geval is, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige bewerking.

Voorbeeld

In onderstaande voorbeeldsessie gaan we ervan uit dat het tekstbestand boodschap.txt² zich in de huidige directory bevindt.

>>> grille = Grille(5, [(0, 0), (1, 0), (1, 2), (1, 4), (3, 3), (4, 2)])
>>> grille.dimensie
5
>>> grille.openingen
{(1, 2), (0, 0), (3, 3), (1, 4), (4, 2), (1, 0)}
>>> print(grille)
O####
O#O#O
#####
###O#
##O##
>>> grille.decodeer('boodschap.txt3')
'East, '
>>> grille.roteer().openingen
{(3, 1), (2, 0), (2, 3), (4, 3), (0, 4), (0, 3)}
>>> print(grille)
###OO
#####
O##O#
#O###
###O#
>>> grille.decodeer('boodschap.txt4')
'West, '
>>> grille.roteer().openingen
{(3, 2), (3, 0), (4, 4), (1, 1), (3, 4), (0, 2)}
>>> print(grille)
##O##
#O###
#####
O#O#O
####O
>>> grille.decodeer('boodschap.txt5')
"home's"
>>> grille.roteer().openingen
{(0, 1), (1, 3), (2, 1), (4, 1), (2, 4), (4, 0)}
>>> print(grille)
#O###
###O#
#O##O
#####
OO###
>>> grille.decodeer('boodschap.txt6')
' best.'
>>> grille.roteer(wijzerzin=False).openingen
{(3, 2), (3, 0), (4, 4), (1, 1), (3, 4), (0, 2)}
>>> print(grille)
##O##
#O###
#####
O#O#O
####O
>>> grille.decodeer('boodschap.txt7')
"home's"

>>> grille1 = Grille(4, ((1, 3), (0, 0), (2, 3), (1, 1)))
>>> grille2 = Grille(4, {(2, 0), (1, 0), (3, 3), (2, 2)})
>>> grille3 = Grille(4, [(3, 0), (2, 3), (2, 0), (1, 1)])
>>> grille4 = Grille(5, ((1, 3), (0, 0), (2, 3), (1, 1)))
>>> grille1 == grille2
True
>>> grille1 == grille3
False
>>> grille1 == grille4
False

>>> grille5 = grille1 + grille3
>>> grille5.dimensie
4
>>> grille5.openingen
{(2, 3), (1, 1)}
>>> print(grille5)
####
#O##
###O
####
>>> grille1 + grille4
Traceback (most recent call last):
AssertionError: ongeldige bewerking