Goochelaar Bob Hummer bedacht een magische kaartentruc die bestaat uit de volgende handelingen:
-
kies willekeurig tien kaarten uit een kaartspel en leg ze allemaal op een stapel met de beeldzijde naar onder
-
neem de bovenste twee kaarten af van de stapel, draai ze samen om en leg ze terug bovenaan de stapel
-
coupeer de stapel kaarten op een willekeurige plaats; bij het couperen van een stapel kaarten wordt de stapel in twee gesplitst, en wordt het bovenste deel van de stapel onder het onderste deel van de stapel geschoven
-
herhaal stappen (2) en (3) zo vaak je wil
-
draai alle kaarten op de even posities om: de tweede, de vierde, de zesde, de achtste en de tiende kaart, waarbij we beginnen tellen vanaf de bovenste kaart
Dit resulteert altijd in een stapel waarvan er vijf kaarten met de beeldzijde naar boven liggen.
Onderstaande figuur toont een uitgewerkt voorbeeld van de kaartentruc, waarbij we de posities van de kaarten in de stapel van boven naar onder genummerd hebben van 1 tot en met 10. Elke kaart wordt voorgesteld met een unieke kleur, en de uitstulping geeft aan of de kaart met de beeldzijde naar boven of naar onder ligt. Stappen (2) en (3) worden in dit voorbeeld drie keer herhaald, waarbij we achtereenvolgens in stap (3) couperen na 4, 5 en 3 kaarten. Uiteindelijk liggen na stap (5) de tweede, de derde, de zesde, de achtste en de negende kaart met de beeldzijde naar boven.

Later bewezen Persi Daconis en Ron Graham dat deze truc algemeen werkt voor een stapel van $$2n$$ kaarten, waarbij er finaal $$n$$ kaarten met de beeldzijde naar boven liggen.
Opgave
Een standaard kaartspel bestaat uit 52 verschillende kaarten die onderverdeeld worden in vier kleuren van elk 13 kaarten: 13 klaveren (♣), 13 ruiten (♦), 13 harten (♥) en 13 schoppen (♠). Klaveren en schoppen zijn zwart, ruiten en harten zijn rood, maar het zijn niet deze fysieke kleuren, maar de soorten die met de term kleur aangeduid worden. Van elke kleur zijn er telkens kaarten met een rang van 2 tot en met 10, een boer, een vrouw, een heer en een aas. Daarnaast bevat een spel soms twee of drie jokers, maar die laten we hier even buiten beschouwing.
We stellen elk van de 52 kaarten van een standaard kaartspel voor als een string (String) die bestaat uit de rang van de kaart, gevolgd door de kleur van de kaart:
-
rangen: 2, 3, 4, 5, 6, 7, 8, 9, 10, J (boer), Q (vrouw), K (heer) en A (aas)
-
kleuren: C (klaveren; ♣), D (ruiten; ♦), H (harten; ♥) en S (schoppen; ♠)
Zo stelt AS bijvoorbeeld schoppenaas voor, 10H hartentien en KC klaverenheer. Bovendien leggen we vast dat de voorstelling van een kaart die met zijn beeldzijde naar boven ligt gebruikmaakt van hoofdletters (bijvoorbeeld AS of 10H), en dat de voorstelling van een kaart die met zijn beeldzijde naar onder ligt gebruikmaakt van kleine letters (bijvoorbeeld as of 10h). Merk op dat het laatste karakter van de voorstelling altijd een hoofdletter of een kleine letter is (geen cijfer) die de kleur van de kaart aanduidt.
De reeksvoorstelling van een stapel kaarten bestaat uit een reeks (Array) met de voorstellingen (String) van de opeenvolgende kaarten uit de stapel, waarbij de bovenste kaart van de stapel het eerste element van de reeks is. Een stapel hoeft niet noodzakelijk alle 52 kaarten van een kaartspel te bevatten, maar mag nooit meerdere keren dezelfde kaart bevatten.
Definieer een klasse Stapel die kan gebruikt worden om stapel kaarten voor te stellen, waarbij sommige kaarten met hun beeldzijde naar boven en de andere met hun beeldzijde naar onder liggen. Bij het aanmaken van een nieuwe stapel kaarten (Stapel) moet de reeksvoorstelling van een stapel met $$n \in \mathbb{N}$$ kaarten doorgegeven worden. Als geen geldige reeksvoorstelling wordt doorgegeven, dan moet een Error opgeworpen worden met de boodschap ongeldige kaarten. Voorts moet je op een stapel kaarten $$s$$ (Stapel) minstens de volgende methoden kunnen aanroepen:
-
Een methode toString waaraan geen argumenten moeten doorgegeven worden. De methode moet een stringvoorstelling (String) van de stapel kaarten $$s$$ teruggeven, die bestaat uit de voorstellingen van de opeenvolgende kaarten van stapel $$s$$ (van boven naar onder), telkens van elkaar gescheiden door een spatie. Hierbij wordt een kaart die met zijn beeldzijde naar boven ligt op de standaard manier voorgesteld. Een kaart die met zijn beeldzijde naar onder ligt wordt voorgesteld door twee sterretjes (**).
-
Een methode selectieOmdraaien waaraan optioneel een reeks (Array) van posities (Number) in stapel $$s$$ moet doorgegeven worden. Hierbij worden de posities van de kaarten van boven naar onder genummerd vanaf 1. De methode mag ervan uitgaan dat alle posities in de gegeven reeks geldig zijn, en dat elke positie hoogstens één keer voorkomt. De methode moet alle kaarten op de aangegeven posities in stapel $$s$$ individueel omdraaien, waarbij de kaarten niet van positie veranderen. Als er geen argument wordt doorgegeven aan de methode, dan moeten alle kaarten in stapel $$s$$ individueel omgedraaid worden, zonder dat de kaarten daarbij van positie veranderen.
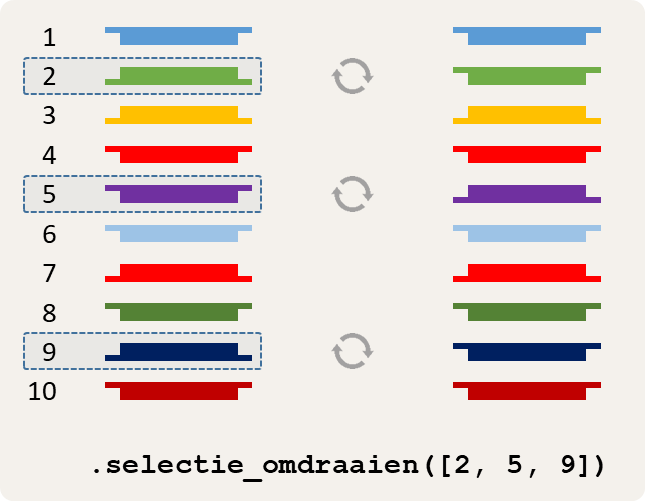
De tweede, de vijfde en de negende kaart individueel omdraaien, zonder dat ze van plaats verwisselen. -
Een methode bovensteOmdraaien waaraan een aantal kaarten $$a \in \mathbb{N}$$ ($$0 \leq a \leq n$$) moet doorgegeven worden. De methode moet de bovenste $$a$$ kaarten afnemen van stapel $$s$$, deze kaarten samen omdraaien en daarna terug bovenaan stapel $$s$$ leggen. Dit is de handeling die uitgevoerd wordt in stap (2) van de kaartentruc met $$a = 2$$.
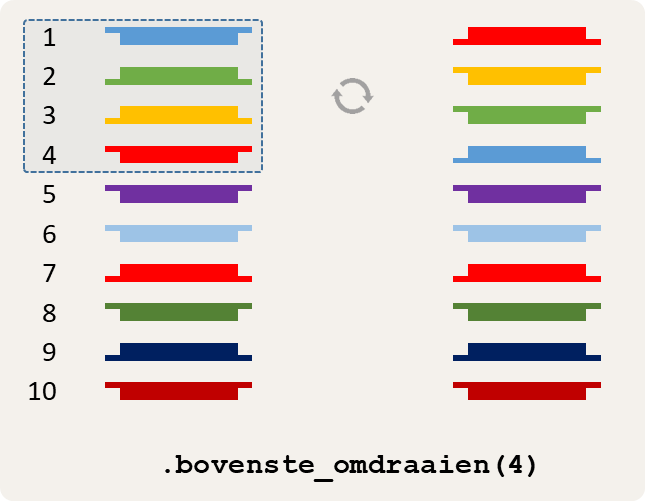
Bovenste vier kaarten omdraaien. -
Een methode couperen waaraan een aantal kaarten $$a \in \mathbb{N}$$ ($$0 \leq a \leq n$$) moet doorgegeven worden. De methode moet de bovenste $$a$$ kaarten afnemen van stapel $$s$$, en deze kaarten onder de resterende kaarten van stapel $$s$$ schuiven. Dit is de handeling die uitgevoerd wordt in stap (3) van de kaartentruc.
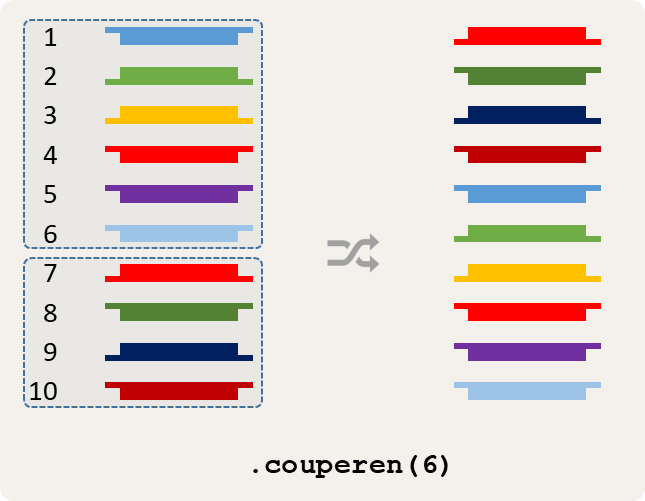
Couperen na zes kaarten.
De methoden selectieOmdraaien, bovensteOmdraaien en couperen moeten allemaal een verwijzing naar stapel $$s$$ teruggeven.
Voorbeeld
Onderstaande code simuleert de opeenvolgende handelingen die in de inleiding werden uitgevoerd bij het voorbeeld van de kaartentruc (zie figuur).
> const kaarten = new Stapel(["AH", "3S", "KC", "4H", "3D", "10H", "8D", "5D", "7C", "QS"])
> kaarten.toString()
"AH 3S KC 4H 3D 10H 8D 5D 7C QS"
> kaarten.selectieOmdraaien().toString()
"** ** ** ** ** ** ** ** ** **"
> kaarten.bovensteOmdraaien(2).toString()
"3S AH ** ** ** ** ** ** ** **"
> kaarten.couperen(4).toString()
"** ** ** ** ** ** 3S AH ** **"
> kaarten.bovensteOmdraaien(2).toString()
"10H 3D ** ** ** ** 3S AH ** **"
> kaarten.couperen(5).toString()
"** 3S AH ** ** 10H 3D ** ** **"
> kaarten.bovensteOmdraaien(2).toString()
"** QS AH ** ** 10H 3D ** ** **"
> kaarten.couperen(3).toString()
"** ** 10H 3D ** ** ** ** QS AH"
> kaarten.selectieOmdraaien([2, 4, 6, 8, 10]).toString()
"** 4H 10H ** ** 5D ** 3S QS **"