De afgeleide in een punt heb je in de lessen wiskunde als volgt gedefinieerd:
Afgeleide in een punt
Indien een functie \(\mathsf{f}\) afleidbaar is in een punt \(\mathsf{a}\), dan wordt de afgeleide in dat punt \(\mathsf{f'(a)}\) gedefinieerd als volgt:
\[\mathsf{f'(a) = \lim_{h\to 0} \dfrac{f(a+h)-f(a)}{h}}\]
Opgave
Schrijf een functie afgeleide(a, f) dat van een functie f de afgeleide in het punt met x-coördinaat a bepaalt.
Een eerste implementatie van het algoritme werkt iteratief en herhaalt de definitie 20 keer. De eerste keer stel je h=1, daarna 0.5, daarna 0.25, enz…
Je geeft de benaderende waarde telkens weer op het scherm, afgerond op 15 cijfers na de komma. Uiteindelijk return je de laatste waarde. Bij probleempunten return je de tekst Niet afleidbaar in dit punt.
Voorbeeld 1
Stel bijvoorbeeld dat f(x) de volgende functie is:
def f(x):
return x**3 - 2
Het uitvoeren van afgeleide( 1, f ) leidt tot:
In iteratie 1 is de benadering: 7.0
In iteratie 2 is de benadering: 4.75
In iteratie 3 is de benadering: 3.8125
In iteratie 4 is de benadering: 3.390625
In iteratie 5 is de benadering: 3.19140625
In iteratie 6 is de benadering: 3.0947265625
In iteratie 7 is de benadering: 3.047119140625
In iteratie 8 is de benadering: 3.02349853515625
In iteratie 9 is de benadering: 3.011734008789062
In iteratie 10 is de benadering: 3.005863189697266
In iteratie 11 is de benadering: 3.002930641174316
In iteratie 12 is de benadering: 3.001465082168579
In iteratie 13 is de benadering: 3.000732481479645
In iteratie 14 is de benadering: 3.000366225838661
In iteratie 15 is de benadering: 3.00018310919404
In iteratie 16 is de benadering: 3.000091553665698
In iteratie 17 is de benadering: 3.000045776600018
In iteratie 18 is de benadering: 3.000022888241801
In iteratie 19 is de benadering: 3.000011444091797
In iteratie 20 is de benadering: 3.000005722045898
De uiteindelijke return waarde bedraagt:
>>> afgeleide( 1, f )
3.000005722045898
Voorbeeld 2
Stel bijvoorbeeld dat f(x) de volgende functie is:
def f(x):
return x**(1/3)
Bij deze functie onstaat duidelijk een probleem…
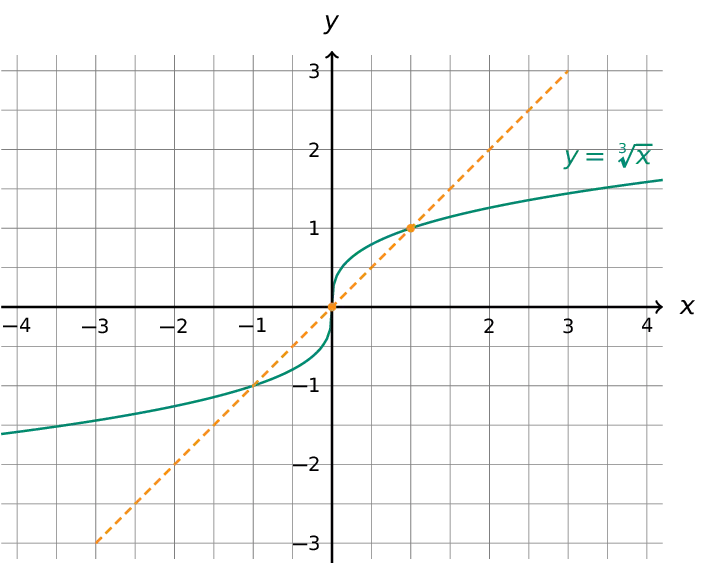
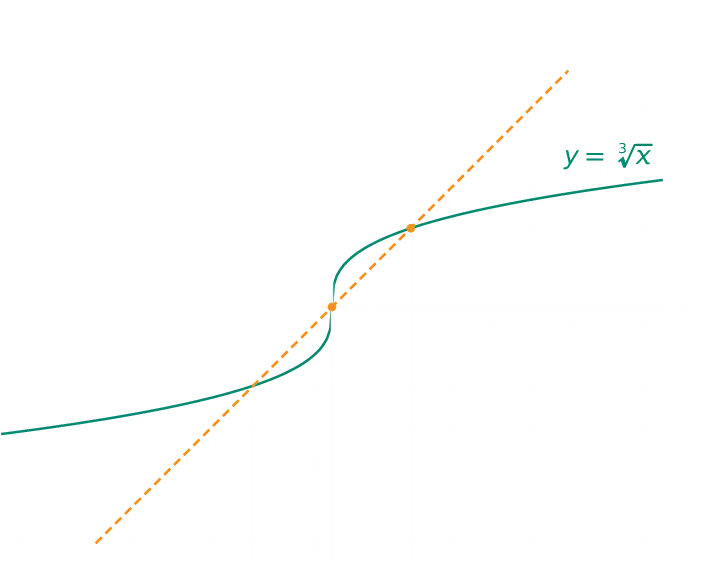
Het uitvoeren van afgeleide( 0, f ) leidt tot:
In iteratie 1 is de benadering: 1.0
In iteratie 2 is de benadering: 1.5874010519682
In iteratie 3 is de benadering: 2.519842099789746
In iteratie 4 is de benadering: 4.0
In iteratie 5 is de benadering: 6.349604207872798
In iteratie 6 is de benadering: 10.079368399158986
In iteratie 7 is de benadering: 16.0
In iteratie 8 is de benadering: 25.398416831491193
In iteratie 9 is de benadering: 40.31747359663594
In iteratie 10 is de benadering: 64.00000000000001
In iteratie 11 is de benadering: 101.59366732596477
In iteratie 12 is de benadering: 161.2698943865438
In iteratie 13 is de benadering: 256.00000000000006
In iteratie 14 is de benadering: 406.37466930385915
In iteratie 15 is de benadering: 645.0795775461752
In iteratie 16 is de benadering: 1024.0000000000002
In iteratie 17 is de benadering: 1625.4986772154366
In iteratie 18 is de benadering: 2580.3183101847007
In iteratie 19 is de benadering: 4096.000000000001
In iteratie 20 is de benadering: 6501.994708861746
De uiteindelijke return waarde bedraagt:
>>> afgeleide( 0, f )
Niet afleidbaar in dit punt