Geohash is een techniek waarmee geografische locaties kunnen gecodeerd worden als een korte reeks letters en cijfers. Zo duidt geohash ezs42 bijvoorbeeld een gebied aan rond de coördinaat (-5.6, 42.6). Geohashes hebben de eigenschap dat je hun nauwkeurigheid kunt variëren en dat je op het einde tekens kunt verwijderen om de code korter te maken (waardoor er geleidelijk ook nauwkeurigheid verloren gaat). Door het gradueel inboeten aan nauwkeurigheid zullen locaties die bij elkaar in de buurt liggen vaak (maar niet altijd) met dezelfde tekens beginnen. Hoe meer gemeenschappelijk tekens vooraan, hoe dichter twee locaties bij elkaar in de buurt liggen.
Stel bijvoorbeeld dat we een gebied rond coördinaat (-5.6, 42.6) — in onderstaande kaart aangeduid met een rode markering — willen voorstellen door een geohash. Daarvoor verdelen we eerst de wereldkaart met een verticale lijn in twee helften die we elk aanduiden met een binaire waarde: 0 (linkerhelft) of 1 (rechterhelft). Omdat de locatie in de linkerhelft ligt, is het eerste bit van de geohash gelijk aan 0.
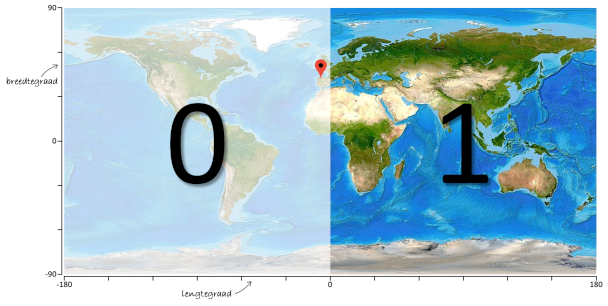
Om de locatie nauwkeuriger aan te duiden, delen we de helft waarin de locatie ligt verder op in twee helften. Nu doen we de verdeling echter met een horizontale lijn en duiden we elke helft opnieuw aan met een binaire waarde: 0 (onderste helft) en 1 (bovenste helft). Omdat de locatie in de bovenste helft ligt, is het tweede bit van de geohash gelijk aan 1.

Daarna delen we de helft waarin de locatie ligt verder op in twee helften, maar dan nu terug met een verticale lijn. Omdat de locatie in de rechterhelft ligt, is het derde bit van de geohash gelijk aan 1.

Door het resterende gebied telkens in twee te verdelen — afwisselend met een verticale en een horizontale lijn — verdubbelen we in elke stap de nauwkeurigheid van de geohash, maar wordt de geohash ook telkens één bit langer.
Opgave
Zet een gegeven geohash om naar coördinaat $$(\lambda, \varphi)$$ met $$\lambda, \varphi \in \mathbb{R}$$. Hierbij geldt dat lengtegraad $$\lambda \in [-180, 180]$$ en breedtegraad $$\varphi \in [-90, 90]$$. We illustreren het algoritme dat je hiervoor moet gebruiken aan de hand van geohash ezs42 die we ook in de inleiding gebruikt hebben.
Eerst zetten we de geohash om naar zijn decimale waarde. Een geohash gebruikt 32 verschillende tekens: de cijfers 0–9 en de letters a–z, behalve de letters a, i, l en o (er wordt geen onderscheid gemaakt tussen hoofdletters en kleine letters). Daardoor kan de geohash geïnterpreteerd worden als een getal in een talstelsel met grondtal 32 (base-32). Een getal $$\left(c_{n}c_{n-1}\ldots c_{2}c_{1}c_{0}\right)_b$$ in een talstelsel met grondtal $$b \in \mathbb{N}_0$$ kan als volgt omgezet worden naar zijn decimale waarde: \[ \sum_{i=0}^{n} \left(c_i\right)_{10} \times b^i \] waarbij de notatie $$\left(c_i\right)_{10}$$ gebruikt wordt voor de decimale waarde van het cijfer $$c_i$$ uit het talstelsel met grondtal $$b$$. De tekens $$\texttt{t}$$ van een geohash krijgen de volgende decimale waarde:
| $$\texttt{t}$$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | b | c | d | e | f | g |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $$\texttt{t}_{10}$$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| $$\texttt{t}$$ | h | j | k | m | n | p | q | r | s | t | u | v | w | x | y | z |
| $$\texttt{t}_{10}$$ | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Zo wordt de decimale waarde van geohash ezs42 met $$b = 32$$ berekend als \[ \left(2 \times 32^{0}\right) + \left(4 \times 32^{1}\right) + \left(24 \times 32^{2}\right) + \left(31 \times 32^{3}\right) + \left(13 \times 32^{4}\right) = 14672002 \] Deze decimale waarde zetten we vervolgens om naar een bitstring met de binaire waarde van de geohash. In Python kan je de ingebouwde functie bin gebruiken om een decimale waarde om te zetten naar zijn binaire waarde.
>>> bin(14672002)
'0b110111111110000010000010'
Bij de omzetting van de decimale waarde naar de bitstring moeten we eventueel voorloopnullen toevoegen aan de binaire waarde, omdat elk teken van een geohash 5 bits codeert ($$2^5 = 32$$). Voor geohash ezs42 krijgen we dan de bitstring 0110111111110000010000010 met 25 bits (één voorloopnul).
Als we nu de bits van de bitstring van links naar rechts nummeren vanaf 0, dan coderen de even bits de lengtegraad (0111110000000) en de oneven bits de breedtegraad (101111001001). Elk van deze bitstrings kan dus gebruikt worden als instructie voor een reeks opeenvolgende opdelingen, waarbij de bits één per één worden afgelopen van links naar rechts. Voor de breedtegraad wordt het interval [-90, 90] in twee gelijke delen verdeeld, waardoor we twee intervallen krijgen: [-90, 0] en [0, 90]. Omdat het eerste bit 1 is, wordt het hogere interval gekozen als het nieuwe interval. Deze procedure wordt herhaald voor alle bits in de bitstring. De uiteindelijk breedtegraad ligt in het midden van het interval dat finaal bekomen wordt. Voor de lengtegraad gebruiken we exact dezelfde procedure, maar vertrekken we van het interval [-180, 180].
Zo is het eerste bit in de bitstring voor de breedtegraad (101111001001) gelijk aan 1, waardoor we weten dat de breedtegraad ergens tussen 0° en 90° ligt. Zonder bijkomende bits zouden we schatten dat de breedtegraad 45° was, wat ons een fout van ±45° oplevert. Omdat er nog meer bits zijn, kunnen we doorgaan met het volgende bit, waarbij elke volgende bit de fout halveert. Onderstaande tabel toont het effect van elke bit. In elke stap wordt de gekozen helft van het interval groen gemarkeerd: bit 0 kiest de onderste helft en bit 1 kiest de bovenste helft. De kolom "breedtegraad" toont de schatting van de breedtegraad als middelpunt van het gekozen interval. Elke volgende bit maakt deze schatting nauwkeuriger.
| positie | bit | ondergrens | midden | bovengrens | breedtegraad | maximale fout |
|---|---|---|---|---|---|---|
| 0 | 1 | -90.000 | 0.000 | 90.000 | 45.000 | 45.000 |
| 1 | 0 | 0.000 | 45.000 | 90.000 | 22.500 | 22.500 |
| 2 | 1 | 0.000 | 22.500 | 45.000 | 33.750 | 11.250 |
| 3 | 1 | 22.500 | 33.750 | 45.000 | 39.375 | 5.625 |
| 4 | 1 | 33.750 | 39.375 | 45.000 | 42.188 | 2.813 |
| 5 | 1 | 39.375 | 42.188 | 45.000 | 43.594 | 1.406 |
| 6 | 0 | 42.188 | 43.594 | 45.000 | 42.891 | 0.703 |
| 7 | 0 | 42.188 | 42.891 | 43.594 | 42.539 | 0.352 |
| 8 | 1 | 42.188 | 42.539 | 42.891 | 42.715 | 0.176 |
| 9 | 0 | 42.539 | 42.715 | 42.891 | 42.627 | 0.088 |
| 10 | 0 | 42.539 | 42.627 | 42.715 | 42.583 | 0.044 |
| 11 | 1 | 42.539 | 42.583 | 42.627 | 42.605 | 0.022 |
Op dezelfde manier kunnen we ook een schatting maken van de lengtegraad (bitstring 0111110000000).
| positie | bit | ondergrens | midden | bovengrens | lengtegraad | maximale fout |
|---|---|---|---|---|---|---|
| 0 | 0 | -180.000 | 0.000 | 180.000 | -90.000 | 90.000 |
| 1 | 1 | -180.000 | -90.000 | 0.000 | -45.000 | 45.000 |
| 2 | 1 | -90.000 | -45.000 | 0.000 | -22.500 | 22.500 |
| 3 | 1 | -45.000 | -22.500 | 0.000 | -11.250 | 11.250 |
| 4 | 1 | -22.5000 | -11.250 | 0.000 | -5.625 | 5.625 |
| 5 | 1 | -11.250 | -5.625 | 0.000 | -2.813 | 2.813 |
| 6 | 0 | -5.625 | -2.813 | 0.00 | -4.219 | 1.406 |
| 7 | 0 | -5.625 | -4.219 | -2.813 | -4.922 | 0.703 |
| 8 | 0 | -5.625 | -4.922 | -4.219 | -5.273 | 0.352 |
| 9 | 0 | -5.625 | -5.273 | -4.922 | -5.449 | 0.176 |
| 10 | 0 | -5.625 | -5.449 | -5.273 | -5.537 | 0.088 |
| 11 | 0 | -5.625 | -5.537 | -5.449 | -5.581 | 0.044 |
| 12 | 0 | -5.625 | -5.581 | -5.537 | -5.603 | 0.022 |
Gevraagd wordt:
-
Schrijf een functie geo2dec waaraan een geohash (str) moet doorgegeven worden. De functie moet de decimale waarde (int) van de gegeven geohash teruggeven.
-
Schrijf een functie geo2bin waaraan een geohash (str) moet doorgegeven worden. De functie moet de bitstring (str) voor de gegeven geohash teruggeven.
-
Schrijf een functie unravel waaraan een string (str) moet doorgegeven worden. Als we de posities van de karakters in de gegeven string van links naar rechts nummeren vanaf 0, dan moet de functie een tuple (tuple) met twee strings (str) teruggeven, waarbij de eerste string gevormd wordt door de karakters op de even posities en de tweede door de karakters op de oneven posities.
-
Schrijf een functie bin2coord waaraan drie argumenten moeten doorgegeven worden: i) een bitstring (str), ii) de ondergrens $$l$$ (float) van een interval en iii) de bovengrens $$u$$ (float) van het interval. De functie moet een tuple (tuple) met twee getallen $$l', u' \in \mathbb{R}$$ (float) teruggeven dat het interval $$[l', u']$$ beschrijft dat bekomen wordt door telkens de helft van het gegeven interval $$[l, u]$$ te kiezen volgens de instructies van de gegeven bitstring.
-
Schrijf een functie geo2coord waaraan een geohash (str) moet doorgegeven worden. De functie moet de cöordinaat $$(\lambda, \varphi)$$ teruggeven die correspondeert met de gegeven geohash als een tuple (tuple) met twee getallen $$\lambda, \varphi \in \mathbb{R}$$ (float).
Voorbeeld
>>> geo2dec('ezs42')
14672002
>>> geo2dec('DRUGGED')
13684424108
>>> geo2dec('ZUR1CH')
1068205424
>>> geo2bin('ezs42')
'0110111111110000010000010'
>>> geo2bin('DRUGGED')
'01100101111101001111011110110101100'
>>> geo2bin('ZUR1CH')
'111111101010111000010101110000'
>>> unravel('0110111111110000010000010')
('0111110000000', '101111001001')
>>> unravel('01100101111101001111011110110101100')
('010011001101110010', '10111110111101110')
>>> unravel('111111101010111000010101110000')
('111111110000100', '111000100111100')
>>> bin2coord('0111110000000', -180, 180)
(-5.625, -5.5810546875)
>>> bin2coord('101111001001', -90, 90)
(42.5830078125, 42.626953125)
>>> bin2coord('010011001101110010', -180, 180)
(-71.91375732421875, -71.91238403320312)
>>> bin2coord('10111110111101110', -90, 90)
(44.27215576171875, 44.273529052734375)
>>> bin2coord('111111110000100', -180, 180)
(178.6376953125, 178.648681640625)
>>> bin2coord('111000100111100', -90, 90)
(69.23583984375, 69.2413330078125)
>>> geo2coord('ezs42')
(-5.60302734375, 42.60498046875)
>>> geo2coord('DRUGGED')
(-71.91307067871094, 44.27284240722656)
>>> geo2coord('ZUR1CH')
(178.6431884765625, 69.23858642578125)