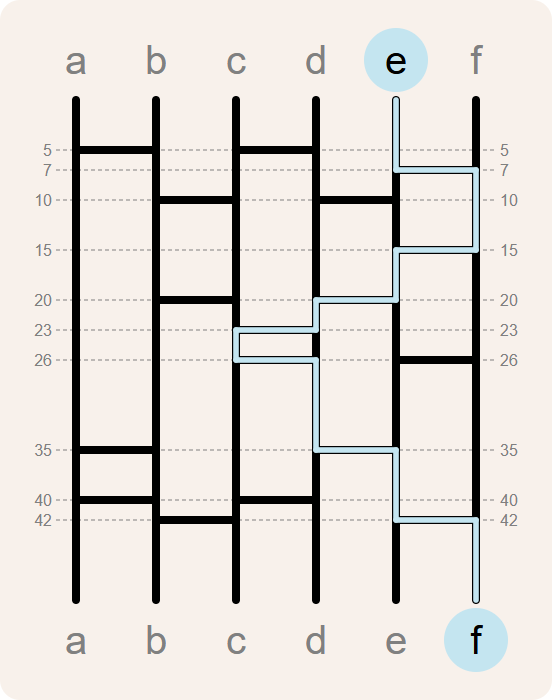
Spookbeen is een methode om de items uit twee groepen van gelijke grootte op een willekeurige manier aan elkaar te koppelen. Ze kan bijvoorbeeld gebruikt worden om $$n$$ taken willekeurig toe te wijzen aan $$n$$ personen. In Japan staat de methode bekend als amidakuji.

Eerst wordt er een diagram getekend dat bestaat uit $$n$$ verticale lijnen. Zo'n verticale lijn wordt een stam genoemd. Daarna wordt een willekeurig aantal "benen" toegevoegd aan het diagram. Een been is een horizontale lijn die twee aangrenzende stammen met elkaar verbindt. Het is niet toegelaten dat een stam op dezelfde hoogte zowel een been naar links als een been naar rechts heeft.

Voorbeelddiagram van een amidakuji waarmee de items van twee groepen van $$n=6$$ items aan elkaar gekoppeld kunnen worden. De $$n=6$$ stammen (verticale lijnen) worden van links naar rechts gelabeld met de letters a–f. Er zijn 17 benen die telkens twee aangrenzende stammen met elkaar verbinden.

Daarna wordt het middelste deel van het diagram afgedekt om de benen te verbergen. Enkel de boven- en onderkant van elke stam is zichtbaar, maar het valt niet te zeggen welke bovenkant met welke onderkant verbonden wordt. Elke taak wordt aan de onderkant van een stam toegekend, en de personen mogen elk aan de bovenkant van een stam gaan staan (geen twee personen aan dezelfde stam).

Het middelste deel van het diagram wordt afgedekt om de benen te verbergen. Enkel de boven- en onderkant van elke stam is zichtbaar, maar het valt niet te zeggen welke bovenkant met welke onderkant verbonden wordt.

Nu worden de spookbenen onthuld en kan elke persoon vanaf de bovenkant van het diagram een route volgen naar de onderkant van het diagram. Daarbij moeten ze afslaan bij elk been dat ze tegenkomen, naar de aangrenzende stam springen en verder naar beneden gaan. Wanneer een persoon de onderkant van het diagram bereikt, wordt zo een link gelegd tussen die persoon en de taak die daar te vinden is.

Een route doorheen een amidakuji start bij een stam aan de bovenkant van het diagram en loopt naar de onderkant van het diagram. Daarbij moet de route afslaan bij elk been dat wordt tegenkomen, naar de aangrenzende stam springen en verder naar beneden gaan. Wanneer de onderkant van het diagram bereikt, wordt zo een link gelegd tussen een stam de bovenkant van het diagram en een stam aan de onderkant van het diagram.

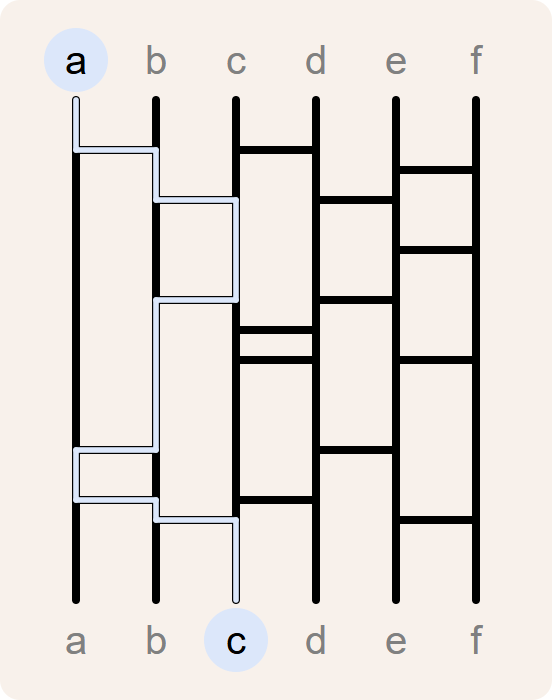
Het voordeel van deze methode is dat ze werkt voor elke twee groepen van dezelfde grootte, waarbij de items uit de twee groepen op betrouwbare wijze aan elkaar gekoppeld worden. Het maakt bovendien niet uit hoeveel benen er toegevoegd worden.

Opgave

Het diagram van een amidakuji wordt beschreven in een tekstbestand. Daarbij wordt elke stam gelabeld met een unieke letter. De bovenkant van het diagram bevindt zich op afstand 0 en de afstand stijgt naarmate we verder naar de onderkant van het diagram gaan. Elke regel van het tekstbestand beschrijft een been van de amidakuji aan de hand van drie velden die van elkaar gescheiden worden door een spatie. De eerste twee velden bevatten de labels van de aangrenzende stammen die door het been met elkaar verbonden worden. Het derde veld bevat de afstand van het been tot de bovenkant van het diagram. Die afstand is steeds een natuurlijk getal. Als de benen van de amidakuji die we als voorbeeld gebruikt hebben zich op deze afstanden bevinden

Het voorbeelddiagram van een amidakuji waarbij elke stam gelabeld wordt met een unieke letter en waarbij voor alle benen ook hun afstand tot de bovenkant van het diagram aangeduid wordt. De bovenkant van het diagram bevindt zich op afstand 0 en de afstand stijgt naarmate we verder naar de onderkant van het diagram gaan.

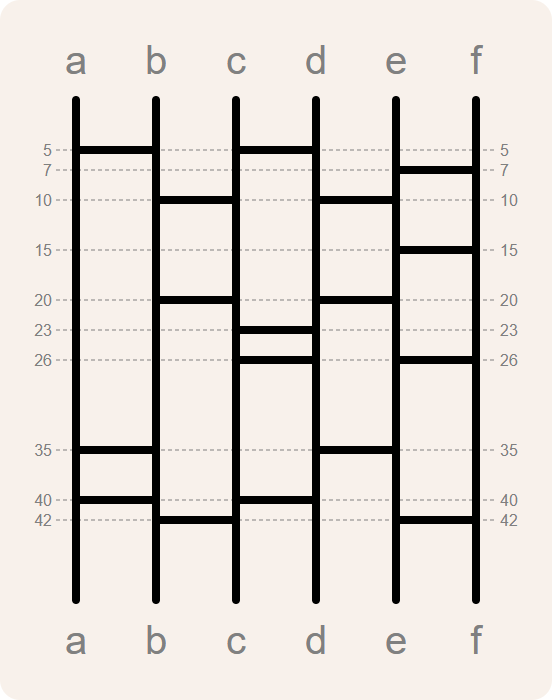
dan kan het diagram beschreven worden door dit tekstbestand (amidakuji.txt¹)

a b 5
c d 5
e f 7
b c 10
d e 10
e f 15
b c 20
d e 20
c d 23
c d 26
e f 26
a b 35
d e 35
a b 40
c d 40
b c 42
e f 42

Gevraagd wordt:

Schrijf een functie lees_aftakkingen waaraan de locatie (str) moet doorgegeven worden van een tekstbestand dat het diagram van een amidakuji beschrijft. Als er in het diagram een stam voorkomt die op dezelfde hoogte zowel een been naar links als een been naar rechts heeft, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige amidakuji. Anders moet de dictionaryvoorstelling van de amidakuji teruggegeven worden. Dit is een dictionary (dict) waarvan de sleutels gevormd worden door de labels (str) van de stammen van de amidakuji. Deze dictionary moet het label (str) van een stam afbeelden op een dictionary (dict) die de hoogte (int) van elk been dat aftakt van de stam afbeeldt op het label (str) van de aangrenzende stam waar het been naar toe leidt.
Schrijf een functie route waaraan twee argumenten moeten doorgegeven worden: i) het label $$s$$ (str) van een stam en ii) de dictionaryvoorstelling (dict) van een amidakuji. Als de amidakuji geen stam heeft met label $$s$$, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige stam. Anders moet de functie de route teruggeven die aan de bovenkant van het diagram start bij stam $$s$$ en doorheen de amidakuji loopt tot aan de onderkant van het diagram. De route wordt beschreven als een lijst (list) met de opeenvolgende sprongen naar aangrenzende stammen langs de route. Een sprong wordt beschreven als een tuple met twee elementen: i) de afstand (int) waarop de route naar een aangrenzende stam springt en ii) het label van de aangrenzende stam waar de route naar springt. De route begint door op afstand 0 te springen naar stam $$s$$. De functie mag de dictionaryvoorstelling (dict) van de amidakuji die eraan doorgegeven wordt niet wijzigen.
Schrijf een functie amidakuji waaraan de dictionaryvoorstelling (dict) van een amidakuji moet doorgegeven worden. De functie moet een dictionary (dict) teruggeven die het label (str) van elke stam van de amidakuji afbeeldt op het label (str) van het eindpunt (ook een stam) van de route doorheen de amidakuji die aan de bovenkant start bij die stam. De functie mag de dictionaryvoorstelling (dict) van de amidakuji die eraan doorgegeven wordt niet wijzigen.

Voorbeeld

In onderstaande voorbeeldsessie gaan we ervan uit dat het tekstbestand amidakuji.txt² zich in de huidige directory bevindt. Daarin wordt het diagram beschreven van de amidakuji die we in deze opgave als voorbeeld gebruikt hebben.

        >>> aftakkingen = lees_aftakkingen('amidakuji.txt3')
>>> aftakkingen['a']
{5: 'b', 35: 'b', 40: 'b'}
>>> aftakkingen['b']
{5: 'a', 10: 'c', 20: 'c', 35: 'a', 40: 'a', 42: 'c'}
>>> aftakkingen['c']
{5: 'd', 10: 'b', 20: 'b', 23: 'd', 26: 'd', 40: 'd', 42: 'b'}
>>> aftakkingen['d']
{5: 'c', 10: 'e', 20: 'e', 23: 'c', 26: 'c', 35: 'e', 40: 'c'}
>>> aftakkingen['e']
{7: 'f', 10: 'd', 15: 'f', 20: 'd', 26: 'f', 35: 'd', 42: 'f'}
>>> aftakkingen['f']
{7: 'e', 15: 'e', 26: 'e', 42: 'e'}

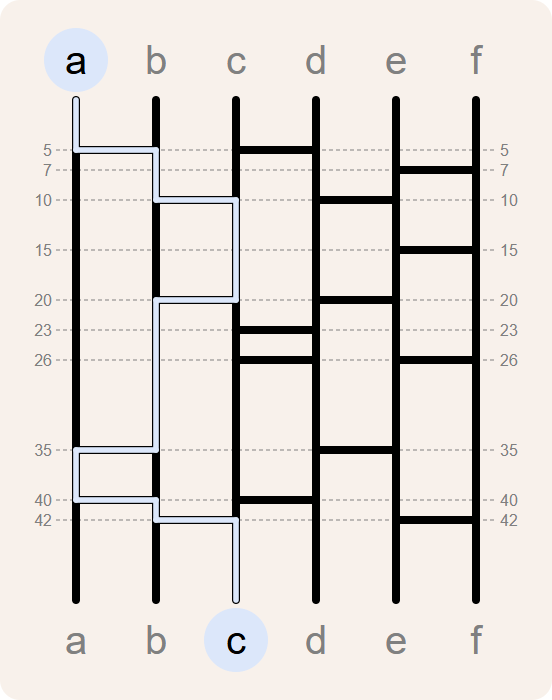
>>> route('a', aftakkingen)
[(0, 'a'), (5, 'b'), (10, 'c'), (20, 'b'), (35, 'a'), (40, 'b'), (42, 'c')]
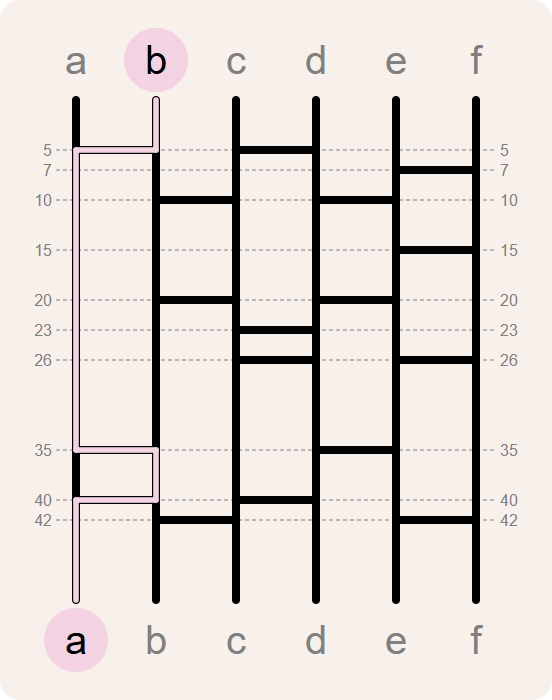
>>> route('b', aftakkingen)
[(0, 'b'), (5, 'a'), (35, 'b'), (40, 'a')]
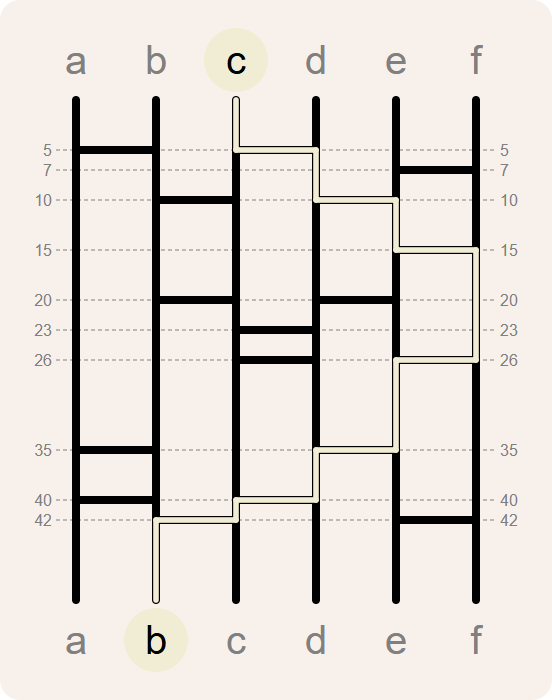
>>> route('c', aftakkingen)
[(0, 'c'), (5, 'd'), (10, 'e'), (15, 'f'), (26, 'e'), (35, 'd'), (40, 'c'), (42, 'b')]
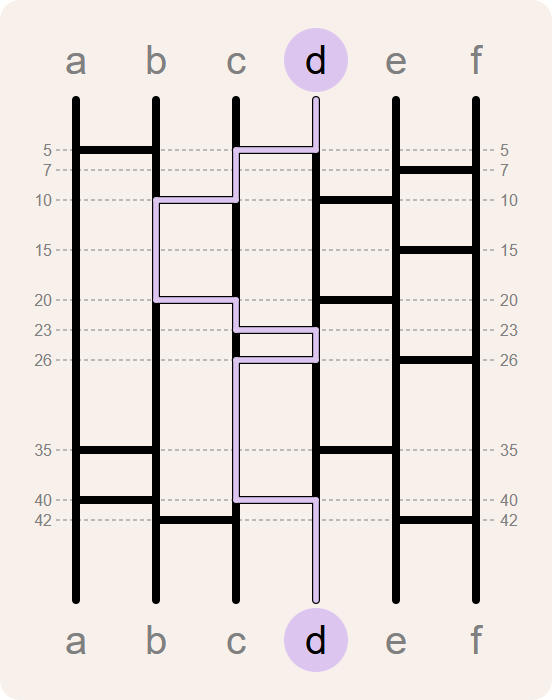
>>> route('d', aftakkingen)
[(0, 'd'), (5, 'c'), (10, 'b'), (20, 'c'), (23, 'd'), (26, 'c'), (40, 'd')]
>>> route('e', aftakkingen)
[(0, 'e'), (7, 'f'), (15, 'e'), (20, 'd'), (23, 'c'), (26, 'd'), (35, 'e'), (42, 'f')]
>>> route('f', aftakkingen)
[(0, 'f'), (7, 'e'), (10, 'd'), (20, 'e'), (26, 'f'), (42, 'e')]

>>> amidakuji(aftakkingen)
{'a': 'c', 'b': 'a', 'c': 'b', 'd': 'd', 'e': 'f', 'f': 'e'}

Dit zijn de routes doorheen de amidakuji die starten bij de verschillende stammen aan de bovenkant van het diagram .

De route doorheen de amidakuji die begint bij stam a en eindigt bij stam c.

De route doorheen de amidakuji die begint bij stam b en eindigt bij stam a.

De route doorheen de amidakuji die begint bij stam c en eindigt bij stam b.

De route doorheen de amidakuji die begint bij stam d en eindigt bij stam d.

De route doorheen de amidakuji die begint bij stam e en eindigt bij stam f.

De route doorheen de amidakuji die begint bij stam f en eindigt bij stam e.