Naburige getallen is een puzzel die gebruik maakt van een rechthoekig $$m \times n$$ rooster met $$m$$ rijen en $$n$$ kolommen. Initieel zijn de cellen van het rooster allemaal leeg. Het doel is om de cijfers 1 tot en met 9 in te vullen in de cellen van het rooster, waarbij de som van alle cijfers in het rooster zo groot mogelijk moet zijn. Hierbij gelden de volgende regels:

• de cellen van het rooster kunnen enkel ingevuld worden met de cijfers 1 tot en met 9

• het cijfer 1 kan in elke cel ingevuld worden

• het cijfer 2 kan in elke cel ingevuld worden die een naburige cel heeft waarin het cijfer 1 is ingevuld

• het cijfer 3 kan in elke cel ingevuld worden die naburige cellen heeft waarin de cijfers 2 en 1 zijn ingevuld

• …

• het cijfer 9 kan in elke cel ingevuld worden die naburige cellen heeft waarin de cijfers 8, 7, 6, 5, 4, 3, 2 en 1 zijn ingevuld

• naburige cellen zijn cellen die horizontaal, verticaal of diagonaal raken aan een cel (elke cel heeft dus maximaal 8 naburige cellen)

• er is geen beperking op het aantal keer dat elk cijfer van 1 tot en met 9 mag ingevuld worden — behalve dat ze moeten voldoen aan bovenstaande regels — en je bent niet verplicht om alle cijfers in te vullen

Voor gegeven dimensies van een rechthoekig rooster is het best mogelijk dat er meerdere optimale oplossingen zijn (oplossingen die eenzelfde maximale som opleveren). Hieronder geven we je alvast een voorbeeld van een geldige oplossing met som 427. Dit is de meest optimale oplossing die momenteel gekend is voor een $$10 \times 10$$ rooster.

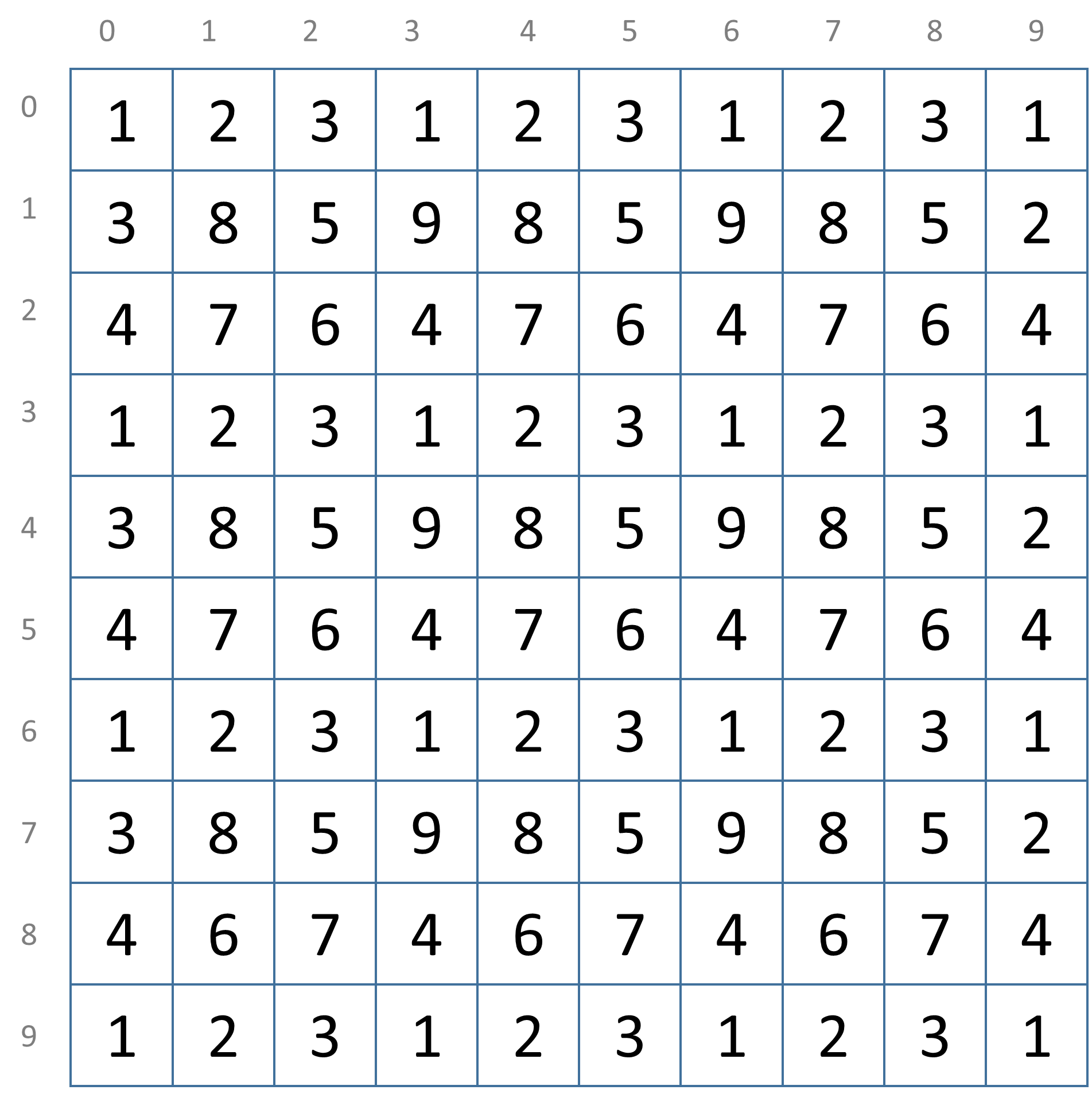
Opgave

Het vinden van optimale oplossingen voor gegeven dimensies van een rechthoekig rooster is een ontzettend uitdagend probleem. Voor deze opgave beperken we ons tot het controleren of een rechthoekig rooster dat ingevuld werd met gehele getallen wel degelijk een geldige oplossing is voor de puzzel. Met andere woorden, dat het rooster voldoet aan de regels die hierboven opgelijst worden. We gebruiken twee manieren om een rechthoekig $$m \times n$$ rooster voor te stellen dat werd ingevuld met de cijfers van 1 tot 9.

Het rooster kan voorgesteld worden als een string waarin alle cijfers opgelijst worden als we de cellen van het rooster van links naar rechts en van boven naar onder aflopen. Samen met deze string moet ook het aantal kolommen gegeven worden, om het rooster op een eenduidige manier vast te leggen. Het aantal cijfers in de string moet uiteraard een veelvoud zijn van het aantal kolommen. We noemen dit de stringvoorstelling van het rooster.

Het rooster kan ook voorgesteld worden als een lijst waarvan de elementen bestaan uit de $$m$$ rijen van het rooster, opgelijst van boven naar onder. Elke rij wordt zelf ook voorgesteld als een lijst met de $$n$$ gehele getallen op die rij, opgelijst van links naar rechts. We noemen dit de lijstvoorstelling van het rooster.

De rijen van het rooster worden van boven naar onder genummerd vanaf nul, en de kolommen van het rooster worden van links naar rechts genummerd vanaf nul. Gevraagd wordt:

• Schrijf een functie lijstvoorstelling waaraan een reeks cijfers (string) en een aantal kolommen (integer) moeten doorgegeven worden die samen de stringvoorstelling van een rooster vormen dat werd ingevuld met de cijfers 1 tot en met 9. De functie moet de lijstvoorstelling van dit rooster teruggeven. Indien de gegeven argumenten geen geldige stringvoorstelling vormen van een rooster dat werd ingevuld met de cijfers 1 tot en met 9, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige stringvoorstelling.

• Schrijf een functie buren waaraan drie argumenten moeten doorgegeven worden: i) een rijnummer (integer), ii) een kolomnummer (integer) en iii) de lijstvoorstelling van een rooster dat werd ingevuld met de getallen 1 tot en met 9. De functie moet een verzameling teruggeven met alle cijfers die ingevuld werden in de naburige cellen van de cel op de gegeven positie in het rooster. Indien de gegeven positie niet binnen het rooster valt, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige positie.

• Schrijf een functie isNaburig waaraan een reeks cijfers (string) en een aantal kolommen (integer) moeten doorgegeven worden die samen de stringvoorstelling van een rooster vormen dat werd ingevuld met de cijfers 1 tot en met 9. De functie moet een Booleaanse waarde teruggeven, die aangeeft of het gegeven rooster een geldige oplossing is voor de puzzel en dus voldoet aan alle regels die hierboven opgelijst worden.  Indien de gegeven argumenten geen geldige stringvoorstelling vormen van een rooster dat werd ingevuld met de cijfers 1 tot en met 9, dan moet de functie een AssertionError opwerpen met de boodschap ongeldige stringvoorstelling.

Voorbeeld

>>> lijstvoorstelling('111222333', 3)
[[1, 1, 1], [2, 2, 2], [3, 3, 3]]
>>> lijstvoorstelling('123321123', 3)
[[1, 2, 3], [3, 2, 1], [1, 2, 3]]
>>> lijstvoorstelling('424313424', 3)
[[4, 2, 4], [3, 1, 3], [4, 2, 4]]
>>> lijstvoorstelling('1541253263631421', 4)
[[1, 5, 4, 1], [2, 5, 3, 2], [6, 3, 6, 3], [1, 4, 2, 1]]
>>> lijstvoorstelling('1541253263631421', 5)
Traceback (most recent call last):
AssertionError: ongeldige stringvoorstelling

>>> rooster = [[1, 5, 4, 1], [2, 5, 3, 2], [6, 3, 6, 3], [1, 4, 2, 1]]
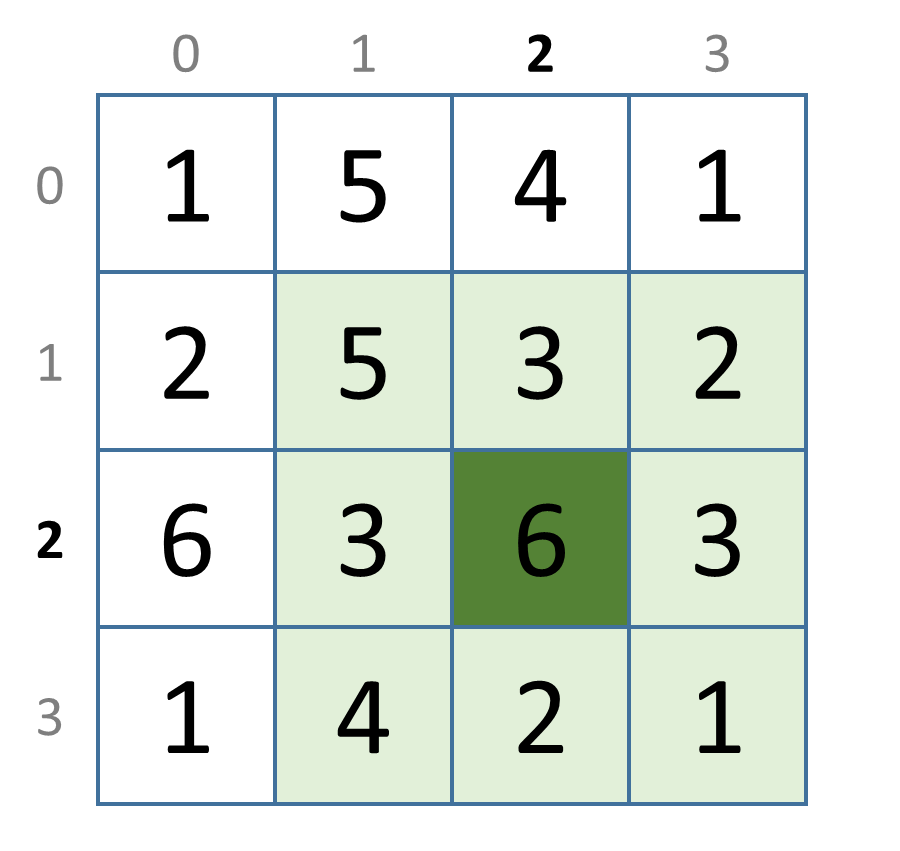
>>> buren(2, 2, rooster)
{1, 2, 3, 4, 5}
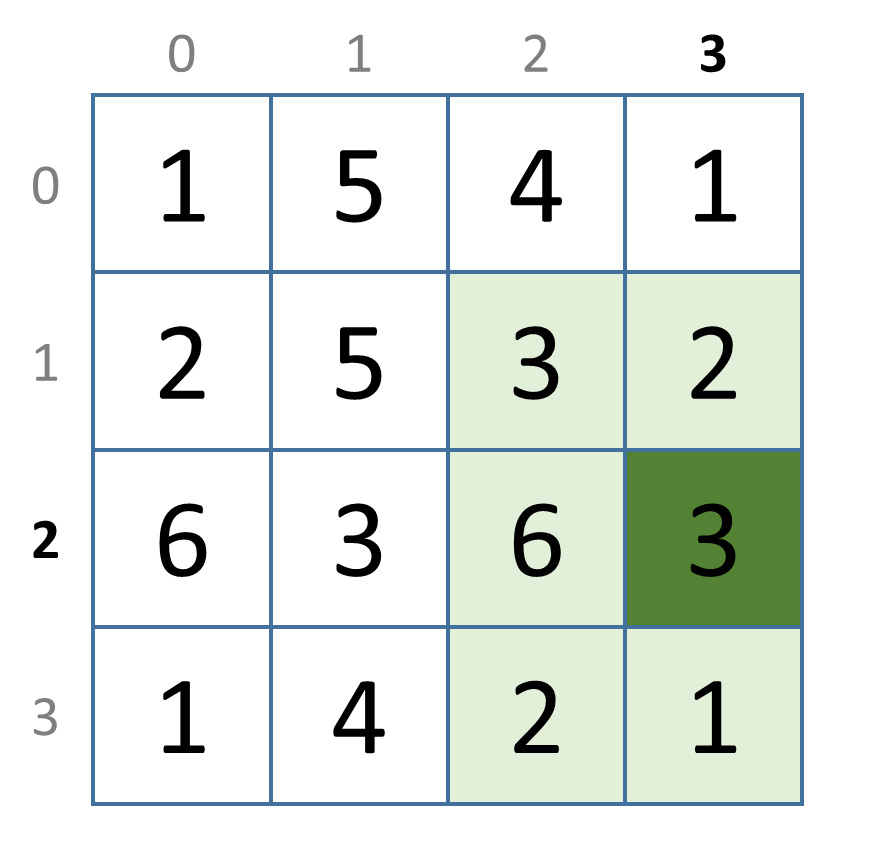
>>> buren(2, 3, rooster)
{1, 2, 3, 6}
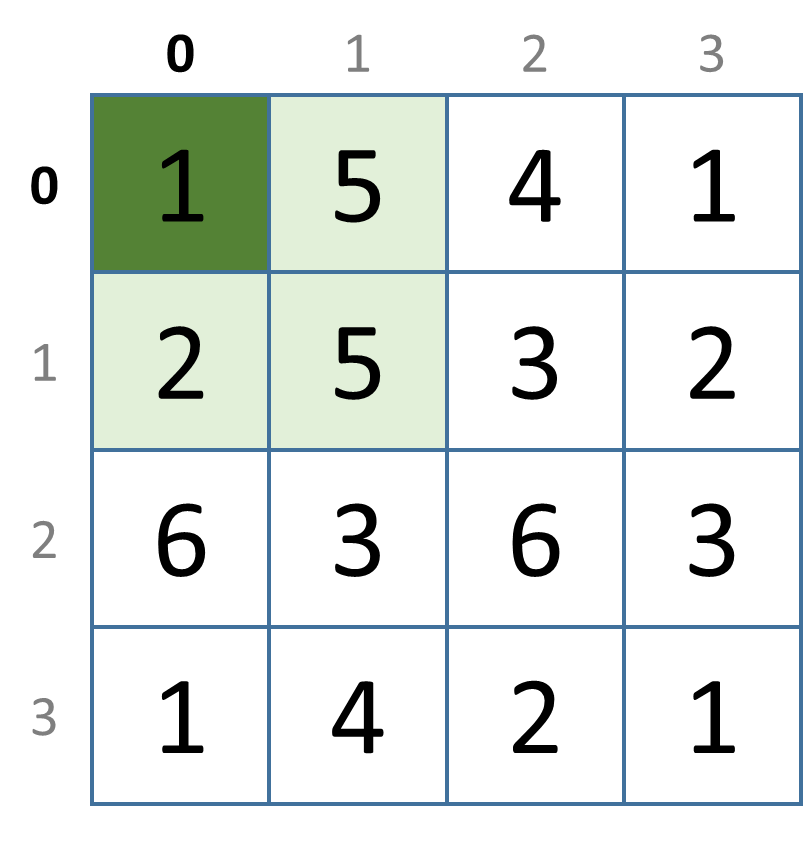
>>> buren(0, 0, rooster)
{2, 5}
>>> buren(4, 4, rooster)
Traceback (most recent call last):
AssertionError: ongeldige positie

>>> isNaburig('111222333', 3)
False
>>> isNaburig('123321123', 3)
True
>>> isNaburig('424313424', 3)
True
>>> isNaburig('1541253263631421', 4)
True
>>> isNaburig('1541253263631421', 5)
Traceback (most recent call last):
AssertionError: ongeldige stringvoorstelling

Hieronder geven we een grafische voorstelling van alle naburige cellen (lichtgroen) voor de cellen (donkergroen) waarmee de functie buren getest wordt in bovenstaande interactieve sessie.