In het verkeersreglement wordt de term ritsen gebruikt om aan te geven dat het verplicht is om op een ordelijke manier in te voegen waar twee rijstroken samenkomen tot één rijstrook. Daarbij moeten de voertuigen beurtelings invoegen op de vrije rijstrook. Dit strookwisselen is noodzakelijk bij knelpunten op autosnelwegen waar de rijbaan met één strook versmalt. Bestuurders op de wegvallende rijstrook moeten dan invoegen in het verkeer van de aanliggende strook.

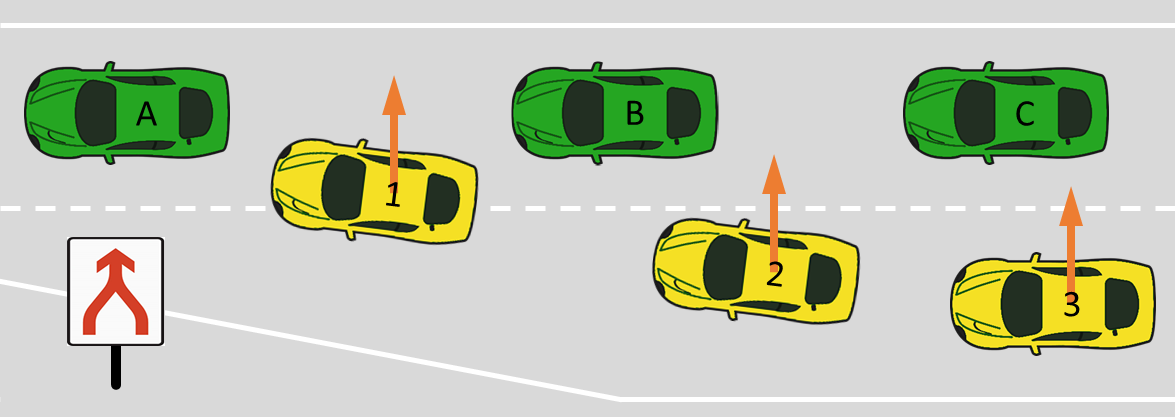
De overheid houdt regelmatig campagnes om het ritsgedrag te bevorderen, omdat bij ritsen al snel irritatie, agressie en gevoelens van onveiligheid ontstaan. Vaak omdat bestuurders die te vroeg invoegen het niet leuk vinden om andere auto's te zien doorrijden tot het einde van de wegvallende rijstrook. Toch is dat doorrijden onderdeel van het gewenste ritsgedrag. Om het ritsgedrag te stimuleren, zijn op veel knelpuntlocaties verkeersborden geplaatst met de teksten "Ritsen na 300 m" en "Ritsen vanaf hier". In België is ritsen vanaf 1 maart 2014 verplicht, en dat op de correcte manier, namelijk vlak voor de wegversmalling. Niet ritsen kan een boete van 55 euro opleveren.

Het mag duidelijk zijn dat ritsen eigenlijk alleen van belang is tijdens drukke periodes, want bij weinig verkeer ontstaan er geen problemen bij het strookwisselen en het invoegen tussen voertuigen op een andere strook, voor zover die aanwezig zijn.

Opgave

We implementeren drie verschillende manieren om de elementen van twee gegeven reeksen (list of tuple) samen te voegen tot één enkele nieuwe lijst (list).

In de drie gevallen verloopt het samenvoegen beurtelings: we voegen het eerste element van de eerste reeks toe aan de nieuwe lijst, daarna het eerste element van de tweede reeks, het tweede element van de eerste reeks, het tweede element van de tweede reeks, enzoverder.

In de drie gevallen gebeurt het samenvoegen ook paarsgewijs: als we het $$i$$-de element van de eerste reeks toevoegen, dan voegen we daarna ook het $$i$$-de element van de tweede reeks toe.

De drie implementaties werken op dezelfde manier als de twee gegeven reeksen die moeten samengevoegd worden even lang zijn. Ze verschillen echter in de manier waarop ze omgaan met reeksen die niet even lang zijn.

Gevraagd wordt:

• Schrijf een functie samenvoegen waaraan twee reeksen (list of tuple) moeten doorgegeven worden. De functie moet een nieuwe lijst (list) teruggeven, waarin de elementen van de twee gegeven reeksen beurtelings en paarsgewijs samengevoegd worden. Het samenvoegen moet stoppen van zodra alle elementen van de kortste reeks zijn toegevoegd aan de nieuwe lijst.

• Schrijf een functie weven waaraan twee reeksen (list of tuple) moeten doorgegeven worden. De functie moet een nieuwe lijst (list) teruggeven, waarin de elementen van de twee gegeven reeksen beurtelings en paarsgewijs samengevoegd worden. Het samenvoegen moet stoppen van zodra alle elementen van de langste reeks zijn toegevoegd aan de nieuwe lijst. Na het laatste element van de kortste reeks wordt terug het eerste element van die reeks toegevoegd, en daarna telkens terug het volgende elementen van de reeks.

• Schrijf een functie ritsen waaraan twee reeksen (list of tuple) moeten doorgegeven worden. De functie moet een nieuwe lijst (list) teruggeven met alle elementen van de twee gegeven reeksen. De functie voegt in die nieuwe lijst eerst beurtelings en paarsgewijs de elementen van de twee gegeven reeksen samen, totdat alle elementen van de kortste reeks zijn toegevoegd. Daarna worden nog de resterende elementen van de langste reeks aan de nieuwe lijst toegevoegd.

Voorbeeld

>>> samenvoegen(('A', 'B', 'C'),  [1, 2, 3])
['A', 1, 'B', 2, 'C', 3]
>>> samenvoegen(['A'], [1, 2, 3, 4])
['A', 1]
>>> samenvoegen(('A', 'B'),  (1, 2, 3, 4))
['A', 1, 'B', 2]
>>> samenvoegen(('A', 'B', 'C'),  [1, 2])
['A', 1, 'B', 2]

>>> weven(('A', 'B', 'C'),  [1, 2, 3])
['A', 1, 'B', 2, 'C', 3]
>>> weven(['A'], [1, 2, 3, 4])
['A', 1, 'A', 2, 'A', 3, 'A', 4]
>>> weven(('A', 'B'),  (1, 2, 3, 4))
['A', 1, 'B', 2, 'A', 3, 'B', 4]
>>> weven(('A', 'B', 'C'),  [1, 2])
['A', 1, 'B', 2, 'C', 1]

>>> ritsen(('A', 'B', 'C'),  [1, 2, 3])
['A', 1, 'B', 2, 'C', 3]
>>> ritsen(['A'], [1, 2, 3, 4])
['A', 1, 2, 3, 4]
>>> ritsen(('A', 'B'),  (1, 2, 3, 4))
['A', 1, 'B', 2, 3, 4]
>>> ritsen(('A', 'B', 'C'),  [1, 2])
['A', 1, 'B', 2, 'C']

Bronnen

• Sugiyama Y, Fukui M, Kikuchi M, Hasabe K, Nakayama A, Nishinari K, Tadaki S, Yukawa S (2008). Traffic jams without bottlenecks — experimental evidence for the physical mechanism of the formation of a jam. New Journal of Physics 10(3), 033001. ³

• Vanderbilt T (2009). Traffic: why we drive the way we do (and what it says about us). Vintage. ⁴