Snake is een eenvoudig computerspelletje dat gespeeld kan worden op onder andere mobiele telefoons. Een variant van het spel, Nibbles, werd een tijdje met MS-DOS1 meegeleverd.
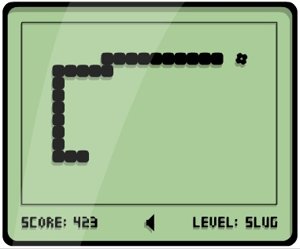
Snake Het doel van het spel is om een slangachtig beest rond te laten lopen in een veld zonder de randen van het veld of de slang zelf te raken. De speler kan het hoofd van de slang naar boven, beneden, links of rechts sturen, de rest van de slang volgt vanzelf. In het veld ligt voedsel. Het eten van dit voedsel zorgt ervoor dat de slang langer wordt, waardoor het besturen van de slang lastiger wordt.
Om de slang van richting te doen veranderen gebruik je de pijltjestoetsen. Opdat de slang zichzelf niet zou opeten, mag je nooit de toetsen ↑ en ↓ (of omgekeerd) na elkaar indrukken. Ook de combinatie ← en → is een dodelijke combintatie.
In deze oefening gaan jullie in een lijst van pijltjestoetsen op zoek naar zo een dodelijke combinatie. Als toetsen gebruiken we <, >, v en ^. Een voorbeeld van een lijst van commando's is:
['<', 'v', '<', '>', '<', '^']Je merkt dat het 4e commando het tegengestelde is van het 3e commando: we hebben dus een reeks van 3 opeenvolgende niet-dodelijke commando's verwerkt.
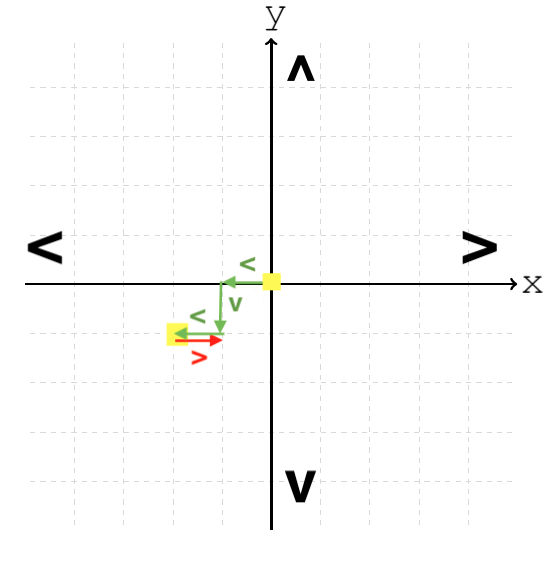
xy Nemen we bovendien aan dat de slang op het scherm op coördinaten $$(0,0)$$ start en dat bij elke pijltjestoets de slang juist één pixel verplaatst wordt, dan is de laatste levende positie van de slang $$(-2,-1)$$.
Let op: de slang blijft gedurende het spel exact 1 pixel groot.
Opgave
Programmeer volgende functies:
- Aan de functie beweeg geef je de coördinaten mee van de slang en een pijltjestoets. De functie verplaatst de slang 1 pixel in de richting van het pijltje en geeft de nieuwe coördinaten terug.
- De functie teruggekeerd vraagt twee pijltjestoetsen in een lijst. De functie geeft True terug indien de twee pijltjes tegengestelde richtingen zijn, bijvoorbeeld '>' en '<'. In het andere geval wordt False terugggegeven.
- laatst_levende_positie vraagt een niet-lege lijst van pijltjestoetsen en geeft een tuple terug met het aantal geldige zetten en de $$x$$- en $$y$$-coördinaat van de laatste levende positie.
Voorbeeld
>>> beweeg((-6, -6), '<') (-7, -6) >>> beweeg((7, 3), '^') (7, 4) >>> teruggekeerd(['^', 'v']) True >>> teruggekeerd(['>', 'v']) False >>> laatste_levende_positie(['>', '<', '^']) (1, 1, 0) >>> laatste_levende_positie(['v', '>', 'v', '<', '^', '^']) (6, 0, 0)Bronnen