Er is iets heel bijzonder aan deze drie reeksen van tien cijfers.
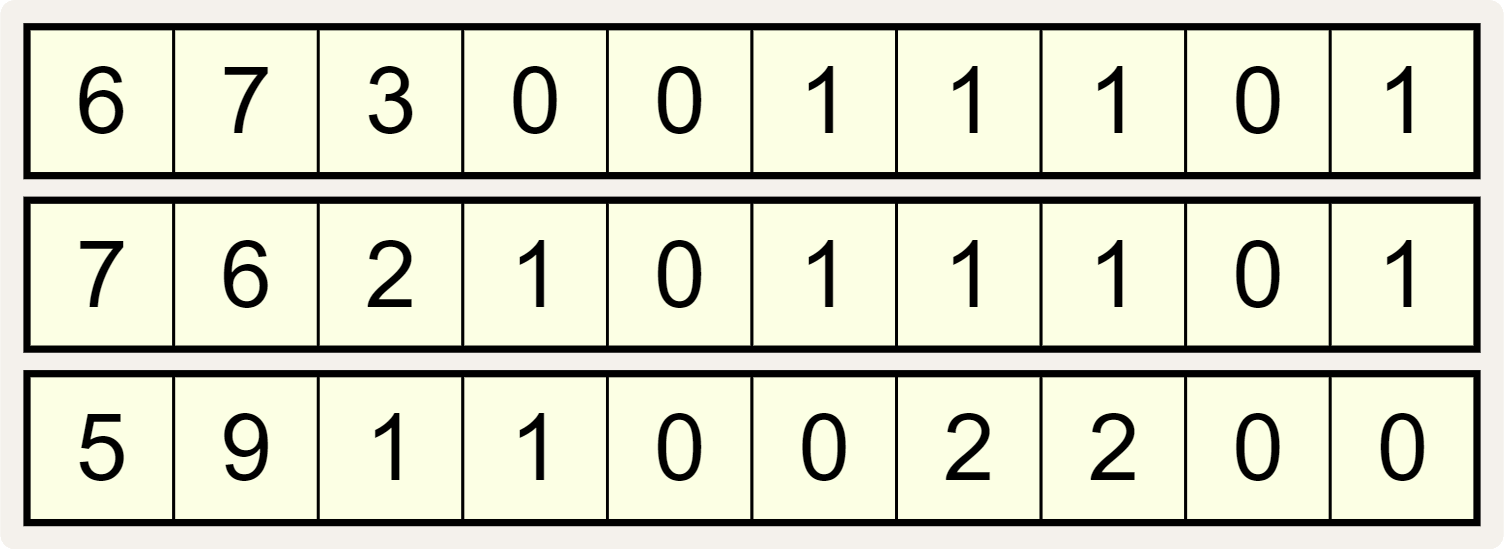
Als we de posities van de cijfers in elke reeks van links naar rechts nummeren vanaf 0 — zoals aangegeven met de grijze cijfers in de hoofding van onderstaande voorstelling van de drie cijferreeksen — dan geeft elk cijfer in kolom $$i$$ ($$i = 0, 1, \ldots, 9)$$ van een cijferreeks aan hoeveel keer het cijfer $$i$$ voorkomt in de twee andere reeksen.
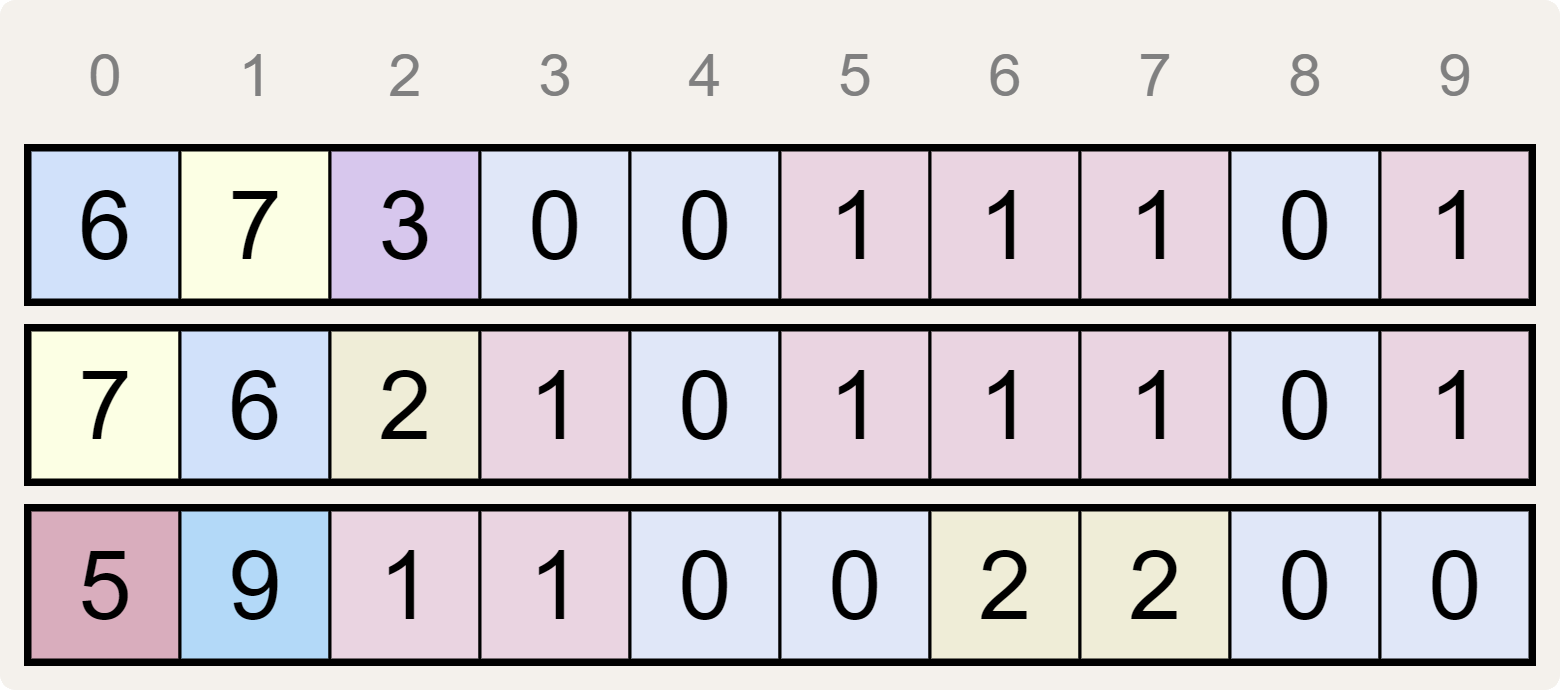
Zo geeft het cijfer 6 aan de linkerkant van de bovenste cijferreeks bijvoorbeeld aan dat het cijfer 0 in totaal 6 keer voorkomt in de onderste twee cijferreeksen. Deze elegante eigenschap geldt ook voor alle andere cijfers in elk van de drie cijferreeksen.
Opgave
De elegante eigenschap geldt echter niet zomaar voor elke combinatie van drie reeksen met tien cijfers. Als we bijvoorbeeld deze drie cijferreeksen nemen
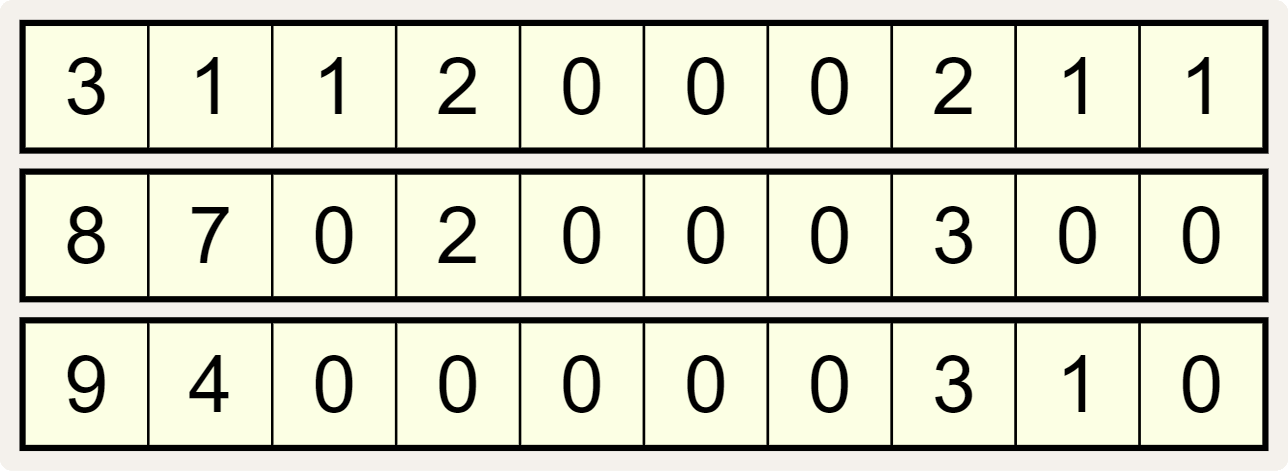
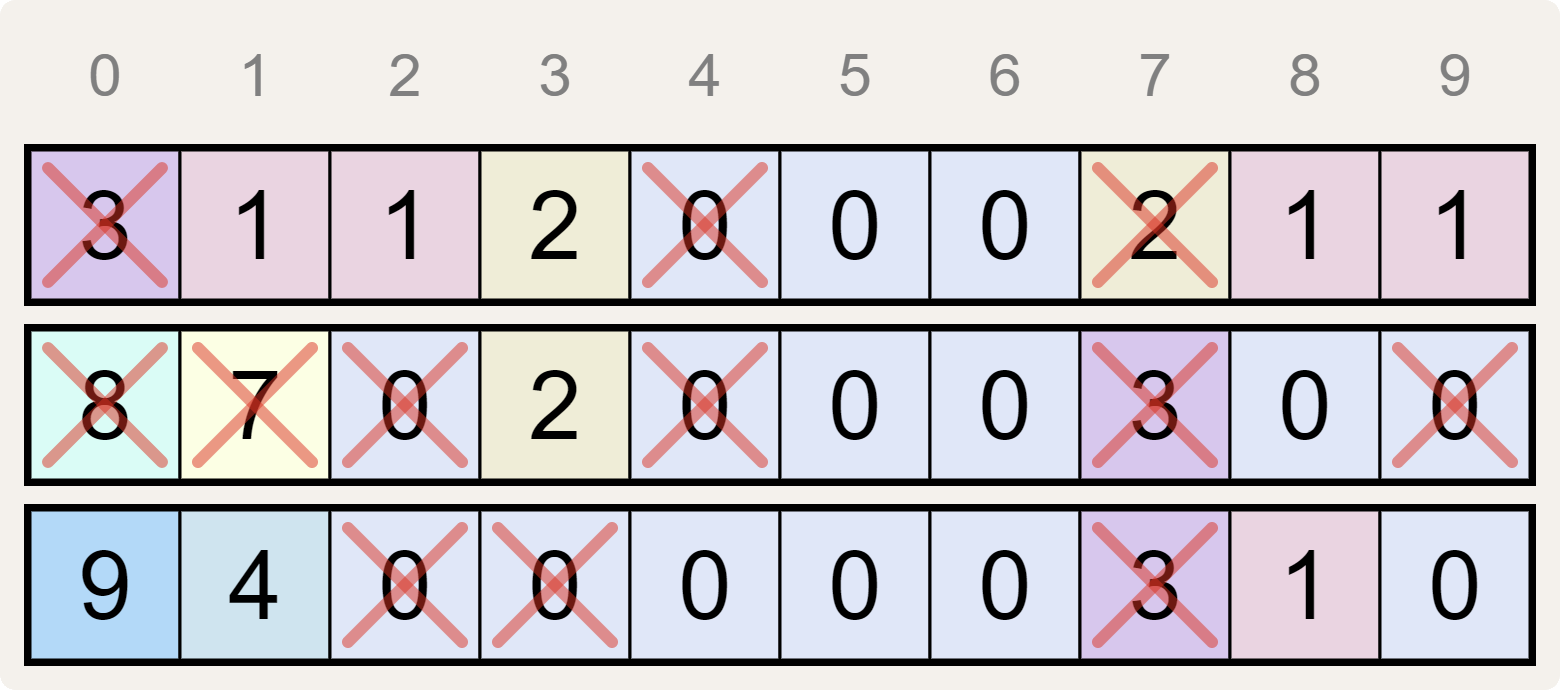
dan hebben we hieronder een rood kruis getrokken door elk cijfer dat niet overeenkomt met het aantal keer dat het cijfer $$i$$ ($$i = 0, 1, \ldots, 9$$) van de corresponderende kolom voorkomt in de andere twee cijferreeksen.
Invoer
Drie reeksen van tien cijfers, elk op een afzonderlijke regel.
Uitvoer
De drie gegeven cijferreeksen, elk op een afzonderlijke regel, waarbij elk cijfer dat niet overeenkomt met het aantal keer dat het cijfer $$i$$ ($$i = 0, 1, \ldots, 9$$) van de corresponderende kolom voorkomt in de andere twee cijferreeksen vervangen werd door de hoofdletter X.
DRY
Don't repeat yourself: vermijd overbodige herhaling in je code.
Don't repeat yourself: vermijd overbodige herhaling in je code.
Voorbeeld
Invoer:
6730011101
7621011101
5911002200Uitvoer:
6730011101
7621011101
5911002200Voorbeeld
Invoer:
3112000211
8702000300
9400000310Uitvoer:
X112X00X11
XXX2X00X0X
94XX000X10