In de vorige opgave hebben we een polymeer voorgesteld als een lijst die de posities van de opeenvolgende monomeren van het polymeer bevat. Elke positie wordt hierbij voorgesteld als een tuple $$(x,y)$$, waarbij $$x,y \in \mathbb{Z}$$. Het eerste monomeer ligt telkens in de oorsprong $$(0,0)$$ van het cartesisch vlak, en de volgende positie ligt telkens één eenheidsstap boven, onder, links of rechts van de vorige positie. Twee monomeren van eenzelfde polymeer kunnen nooit dezelfde positie bezetten.
Opgave
Schrijf een functie toonPolymeer die voor een gegeven lijst van posities van de monomeren van een polymeer (die als argument aan de functie moet doorgegeven worden) de structuur van het polymeer uitschrijft. Hiervoor ga je als volgt te werk:
Definieer een 2-dimensionale matrix $$P$$ (bijvoorbeeld als een lijst van lijsten) om de structuur van het polymeer in op te bouwen. Initieel bevatten alle elementen van deze matrix een string die bestaat uit één enkele spatie.
De even rijen en kolommen van de matrix worden gebruikt om aan te geven waar de monomeren van het polymeer zich bevinden. Monomeren worden aangeduid met de kleine letter o, met uitzondering van het eerste monomeer dat wordt aangeduid met de letter x en het laatste monomeer dat wordt aangeduid met een sterretje (*). Voor elk monomeer op positie $$(x,y)$$ wordt de spatie in de matrix op positie $$P_{i,j}$$ vervangen door het karakter dat het monomeer voorstelt, waarbij\[\begin{cases} \, i = 2\,(y_{\max} - y) \\ \, j = 2\,(x - x_{\min}) \end{cases} \]als we ervan uitgaan dat de rijen en kolommen van de matrix geïndexeerd worden vanaf 0. Hierbij stelt $$x_{\min}$$ de minimale $$x$$-coördinaat van alle monomeren in het polymeer voor, en is $$y_{\max}$$ de maximale $$y$$-coördinaat van alle monomeren in het polymeer.
- Op de oneven rijen en kolommen van de matrix verbinden we de
opeenvolgende monomeren van het polymeer met elkaar. Twee opeenvolgende
monomeren die links en rechts van elkaar liggen worden verbonden door
een koppelteken (-) tussen
de twee posities van de monomeren in de matrix te plaatsen. Twee
opeenvolgende monomeren die boven en onder elkaar liggen worden
verbonden door een verticale streep (|).
Na voorgaande stappen, ziet de matrix die overeenkomt met de
lijstvoorstelling van het polymeer
(0, 0), (1, 0), (2, 0), (3, 0), (4, 0), (4, 1), (4, 2), (4, 3), (3, 3), (2, 3), (2, 2), (2, 1), (3, 1), (3, 2)
er dan bijvoorbeeld als volgt uit
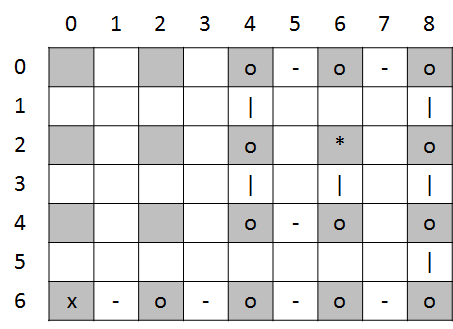
De lege cellen in deze matrixvoorstelling bevatten nog steeds een string die bestaat uit één enkele spatie.
De uitvoer wordt gegenereerd door de rijen van de matrix één voor één uit te schrijven (van boven naar onder), waarbij de verschillende karakters in de kolommen van eenzelfde rij achter elkaar uitgeschreven worden. Het voorgaande voorbeeld levert dan volgende uitvoer op.
o-o-o | | o * o | | | o-o o | x-o-o-o-o
Voorbeeld
>>> polymeer1 = [(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (1, 2), (0, 2),
... (0, 1), (1, 1)]
>>> toonPolymeer(polymeer1)
o-o-o
| |
o-* o
|
x-o-o
>>> polymeer2 = [(0, 0), (1, 0), (2, 0), (2, -1), (3, -1), (4, -1), (4, 0),
... (4, 1), (3, 1), (3, 0)]
>>> toonPolymeer(polymeer2)
o-o
| |
x-o-o * o
| |
o-o-o
>>> polymeer3 = [(0, 0), (0, -1), (1, -1), (1, -2), (1, -3), (1, -4), (0, -4),
... (0, -3), (-1, -3), (-2, -3), (-2, -2), (-2, -1), (-1, -1),
... (-1, -2), (0, -2)]
>>> toonPolymeer(polymeer3)
x
|
o-o o-o
| | |
o o-* o
| |
o-o-o o
| |
o-o