Heel lang geleden leefde er eens een rijke boer die zestien kinderen had, acht bij zijn eerste vrouw die overleden was en acht bij zijn tweede vrouw. Zijn tweede vrouw wilde echter alles in het werk stellen opdat haar oudste zoon de eigendommen van de boer zou erven. Daarom deed ze op een dag het volgende voorstel:

Liefste echtgenoot, je wordt al een dagje ouder. We moeten dringend regelen wie je erfgenaam zal worden. Laat ons de zestien kinderen in een cirkel opstellen. Te beginnen bij één van de kinderen kunnen we dan in wijzerzin elk tiende kind uit de cirkel verwijderen, totdat er slechts één kind overblijft aan wie je je eigendommen zult nalaten.

De boer aanvaarde het voorstel, en zo gezegd, zo gedaan. Nadat het zevende kind uit de cirkel was verwijderd, stelde de boer echter met verbazing vast dat alle kinderen die tot dan toe uit de cirkel waren verwijderd, kinderen waren die hij met zijn eerste vrouw had gekregen. De boer legde daarop prompt de selectieprocedure stil, omdat hij ook al in de gaten had gekregen dat het laatste kind dat hij met zijn eerste vrouw had als volgende aan de beurt was om uit de cirkel verwijderd te worden.

De boer stelde voor om de selectieprocedure te hervatten waar ze gekomen waren nadat het zevende kind uit de cirkel was verwijderd, maar om vanaf dat punt in tegenwijzerzin te beginnen tellen. De vrouw — gedwongen om snel te beslissen — ging direct akkoord omdat de kansen 8 tegen 1 waren in het voordeel van haar kant van de familie. Wie werd uiteindelijk de erfgenaam van de boer?

Als de selectieprocedure wordt toegepast voor een boer die acht kinderen heeft bij elke vrouw, en waarbij elk tiende kind uit de cirkel verwijderd wordt, dan wordt het kind op positie acht de erfgenaam van de boer. De cirkels stellen de kinderen voor. De getallen in de cirkels stelt een nummering van de kinderen voor, die we in wijzerzin hebben genummerd vanaf 1 te beginnen bij het kind bovenaan de cirkel. De getallen aan de binnenkant van de cirkel geven aan in welke volgorde de kinderen uit de cirkel verwijderd worden bij de selectieprocedure.

Opgave

Een boer heeft $$k$$ kinderen bij elk van zijn twee vrouwen. Alle kinderen worden in een cirkel geplaatst, en in wijzerzin genummerd van 1 tot en met $$2k$$. We beginnen in wijzerzin af te tellen vanaf kind nummer 1, waarbij elk $$n$$-de kind uit de cirkel wordt verwijderd. Nadat $$k - 1$$ kinderen uit de cirkel verwijderd werden, wordt verder geteld in tegenwijzerzin. De cirkel wordt steeds kleiner en kleiner, en het laatste kind dat overblijft wordt de erfgenaam van de boer.

Schrijf een functie erfgenaam waaraan de waarden $$k$$ en $$n$$ moeten doorgegeven worden, waarbij je er mag van uitgaan dat $$k \geq 2$$. De functie moet een lijst teruggeven die de volgorde aangeeft waarin de kinderen uit de cirkel verwijderd werden. Het eerst verwijderde kind staat daarbij als eerste in de lijst, en de uiteindelijke erfgenaam als laatste in de lijst. Gebruik de volgnummers waarmee de kinderen in de lijst genummerd werden als elementen in de lijst.

Voorbeeld

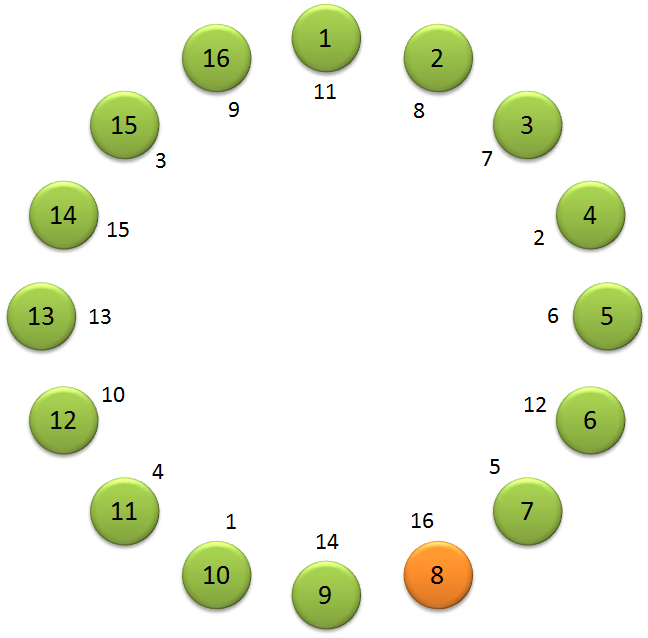
>>> erfgenaam(8, 10)
[10, 4, 15, 11, 7, 5, 3, 2, 16, 12, 1, 6, 13, 9, 14, 8]
>>> erfgenaam(8, 3)
[3, 6, 9, 12, 15, 2, 7, 1, 13, 8, 16, 10, 14, 4, 11, 5]
>>> erfgenaam(10, 5)
[5, 10, 15, 20, 6, 12, 18, 4, 13, 3, 16, 7, 14, 1, 8, 9, 2, 17, 11, 19]