Covariantie en Correlatie

Stel dat X en Y continue toevallig veranderlijken zijn

Voor elk subject i observeren we dus \((X_i,Y_i)\).
Covariantie: hoe variëren \(X_i\) en \(Y_i\) rond hun gemiddelde \((E[X],E[Y])\)?

\[\mbox{Covar}(X,Y)=E[(X-E[X])(Y-E[Y])]\]

De covariantie is dus de verwachte waarde van het product van de afwijking van de X waarde t.o.v. zijn verwachte waarde E\(X\) en de afwijking van de Y waarde t.o.v.zijn verwachte waarde E\(Y\).

We kunnen de covariantie nu ook standardiseren zodat we een maat krijgen die voor elke dataset vergelijkbaar wordt: de correlatie. We doen dit door de covariantie te delen door de standaardafwijking van elke variabele:

\[\mbox{Cor}(X,Y)=\frac{E[(X-E[X])(Y-E[Y])]}{\sqrt{E[(X-E[X])^2}\sqrt{E[(Y-E[Y])^2}}\]

Pearson Correlatie

We introduceren nu een schatter voor de correlatie tussen twee continue toevallig veranderlijken op basis van de data in de steekproef:

\[\mbox{Cor}(X,Y)=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{(n-1)s_{x}s_{y}}\]

We vervangen de verwachte waarden weer door het steekproefgemiddelden \(\bar x\) en \(\bar y\), en, we berekenen het gemiddeld product van de afwijkingen in x en y in de steekproef. Let op dat we hierbij weer corrigeren voor het aantal vrijheidsgraden. We geven elke observatie geen gewicht van 1/n maar van 1/(n-1). We hebben inderdaad het gemiddelde geschat, hier is dat gemiddelde bivariaat (het heeft een x en y coordinaat).

Deze schatter wordt ook wel de Pearson correlatie genoemd en heeft volgende eigenschappen:

Er is een positieve correlatie wanneer \(y\) gemiddeld toeneemt bij een toename van: \(x \ \nearrow \ \Rightarrow \ y \ \nearrow\)
Er is een negatieve correlatie als \(y\) gemiddeld afneemt bij een toename in \(x\): \(x \ \nearrow \ \Rightarrow \ y \ \searrow\)
De correlatie ligt ook altijd tussen -1 en 1

In de figuur 10 wordt de bijdrage weergegeven van individuele metingen in de correlatie. Als punten in het 1ste en 3de kwadrant liggen is er een negatieve bijdrage van de observatie in de correlatie, als ze in het 2de en 4de kwadrant liggen is er een positieve bijdrage.

Figuur 10: Bijdrage van individuele metingen in de correlatie.

We berekenen vervolgens de correlatie voor lengte, gewicht en het log getransformeerde gewicht.

NHANES%>%
  filter(Age >= 18 & Gender=="female") %>%
  select(Weight,Height) %>%
  mutate(log2Weight=Weight%>%log2) %>%
  na.exclude %>%
  cor

##               Weight    Height log2Weight
## Weight     1.0000000 0.2845792  0.9811638
## Height     0.2845792 1.0000000  0.3074578
## log2Weight 0.9811638 0.3074578  1.0000000

Merk op dat:

De correlatie lager is als de data niet worden getransformeerd.
De Pearson correlatie is gevoelig voor outliers!
Gebruik de Pearson correlatie niet voor scheef verdeelde data of data met outliers!

Impact van outliers

In figuur 11 wordt de impact van outliers op de Pearson correlatie geïllustreerd d.m.v. gesimuleerde data met één outlier. We zien dat de correlatie bijna halveert ten gevolge van de outlier!

set.seed(100)
x <- rnorm(20)
simData <- data.frame(x=x,y=x*2 + rnorm(length(x)))
p1 <- simData %>% ggplot(aes(x=x,y=y)) +
  geom_point() +
  ggtitle(paste("cor =",cor(simData[,1],simData[,2]) %>% round(.,2)))

outlier<- rbind(simData,c(2,-4))
p2 <- outlier %>% ggplot(aes(x=x,y=y)) +
  geom_point() +
  ggtitle(paste("cor =",cor(outlier[,1],outlier[,2]) %>% round(.,2)))

grid.arrange(p1,p2,ncol=2)

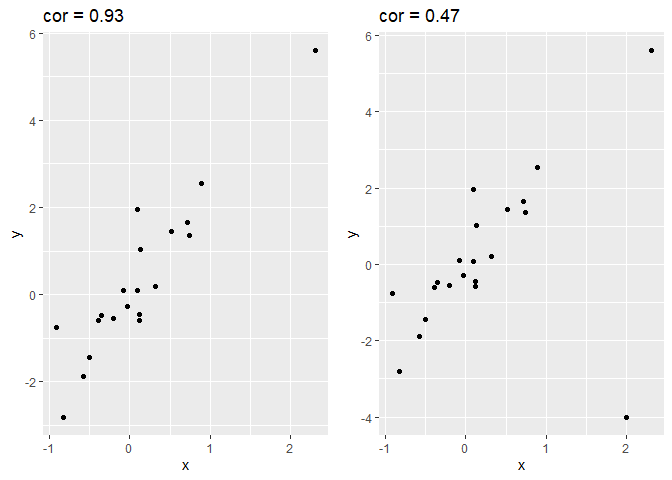
Figuur 11: Correlatie van gesimuleerde data met 1 outlier

De Pearson correlatie pikt enkel linear associatie op

In figuur 12 simuleren we data met een kwadratisch verband en observeren we dat de correlatie bijna nul is!

x <- rnorm(100)
quadratic <- data.frame(x=x,y=x^2 + rnorm(length(x)))
quadratic %>% ggplot(aes(x=x,y=y)) +
  geom_point() +
  ggtitle(paste("cor =",cor(quadratic[,1],quadratic[,2]) %>% round(.,2))) +
  geom_hline(yintercept = mean(quadratic[,2]),col="red") +
    geom_vline(xintercept = mean(quadratic[,1]),col="red")

Figuur 12: Correlatie van gesimuleerde data met een kwadratisch verband. De data in de bovenste kwadranten compenseren elkaar als het ware alsook in de onderste kwadranten (ongeveer evenveel positieve en negatieve bijdragen door de data in de correlatie)

Verschillende groottes van correlatie

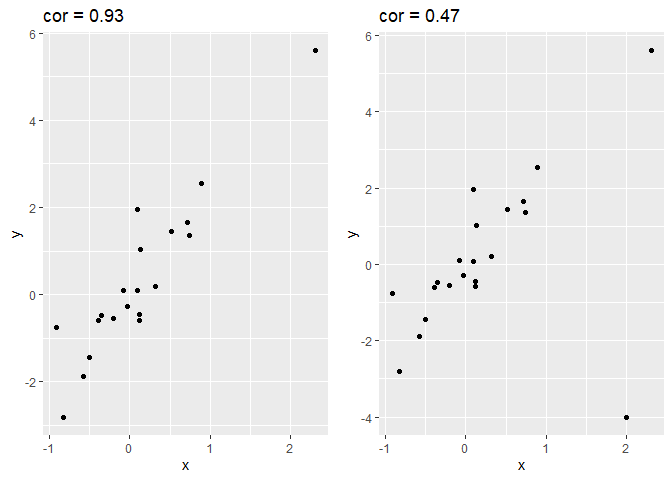
Om een inzicht te krijgen in de grootte van de correlatie, simuleren we data met een verschillende correlatie. We geven telkens de correlatie weer boven de plot. Hoe sterker de correlatie hoe meer de puntenwolk naar een lineair verband toegaat.

Spearman correlatie

De Spearman correlatie is de Pearson correlatie na transformatie van de data naar ranks. Hierdoor wordt deze schatter minder gevoelig voor outliers.

Pearson correlatie

cor(outlier)

##           x         y
## x 1.0000000 0.4682823
## y 0.4682823 1.0000000

Spearman correlatie

cor(outlier,method="spearman")

##           x         y
## x 1.0000000 0.6571429
## y 0.6571429 1.0000000

We verifiëren dat de Spearman correlatie de Pearson correlatie is van rang getransformeerde data. Die wordt bekomen door de observaties te ordenen van klein naar groot en elke observatie te vervangen door zijn rangorde.

rankData<-apply(outlier,2,rank)
cor(rankData)

##           x         y
## x 1.0000000 0.6571429
## y 0.6571429 1.0000000

We berekenen nu de Spearman correlatie in de NHANES studie. We observeren dat de correlatie tussen lengte en gewicht, en lengte en log2 getransformeerd gewicht exact gelijk is. Dat is logisch want de log-transformatie is een monotone transformatie en verandert de ordening van de data dus niet, de ranks van gewicht en deze van het log gewicht zijn identiek!

NHANES%>%
  filter(Age >= 18 & Gender=="female") %>%
  select(Weight,Height) %>%
  mutate(log2Weight=Weight%>%log2) %>%
  na.exclude %>%
  cor(method="spearman")

##               Weight    Height log2Weight
## Weight     1.0000000 0.2892776  1.0000000
## Height     0.2892776 1.0000000  0.2892776
## log2Weight 1.0000000 0.2892776  1.0000000

Bij het interpreteren van correlaties, alsook bij het uitvoeren van regressie-analyses in de volgende secties, zijn de volgende waarschuwingen van zeer groot belang:

Correlaties zijn het makkelijkst te interpreteren tussen 2 groepen Normaal verdeelde observaties. Een kleine training laat immers toe om snel inzicht te krijgen in de grootte van de correlatiecoëfficiënt zonder zich verder over de specifieke verdeling te hoeven bekommeren. In het bijzonder kan men voor Normaal verdeelde observaties visueel inzicht krijgen in de sterkte van de correlatie door een ellips rond de puntenwolk te tekenen die (nagenoeg) alle punten bevat. Als de ellips op een cirkel lijkt, dan is er geen correlatie. Hoe dunner de ellips, hoe sterker de correlatie. De oriëntatie van de ellips geeft hierbij het teken van de correlatie weer.
Voor niet-Normale gegevens hangt de betekenis van een correlatiecoëfficiënt van zekere grootte, nauw samen met de specifieke vorm van de verdeling. Wanneer de 2 variabelen die we onderzoeken niet Normaal verdeeld zijn, dan zijn er 2 mogelijkheden om een zinvolle correlatiecoëfficiënt weer te geven. Variabelen die scheef verdeeld zijn, kan men transformeren (bvb. een log-transformatie) in de hoop dat de getransformeerde gegevens bij benadering Normaal verdeeld zijn en lineair samenhangen.
Merk op dat een correlatiecoëfficiënt van 0 tussen 2 variabelen \(X\) en \(Y\) niet noodzakelijk impliceert dat deze variabelen onafhankelijk zijn. Zie kwadratisch verband! Daarom is het van belang om de aard van samenhang tussen 2 variabelen steeds te onderzoeken via een scatterplot alvorens een correlatiecoëfficiënt te rapporteren. Wanneer het verband monotoon is, maar sterk niet-lineair is, dan is het aangewezen om niet de Pearson correlatiecoëfficiënt, maar Spearman’s correlatiecoëfficiënt te rapporteren. Indien het verband niet-monotoon is, dan zijn correlatiecoëfficiënten niet geschikt en moet men overstappen op meer geavanceerde regressietechnieken.
Bij jonge kinderen is de grootte van hun schoenmaat uiteraard sterk gecorreleerd met hun leescapaciteiten. Dat op zich impliceert echter niet dat het leren van nieuwe woorden hun voeten doet groeien of dat het groeien van hun voeten impliceert dat ze beter kunnen lezen. Ook algemeen hoeft een correlatie tussen 2 variabelen niet te impliceren dat er een causaal verband is. De relatie tussen 2 metingen kan immers sterk verstoord worden door confounders (bvb. de leeftijd in bovenstaand voorbeeld). Hoewel dit overduidelijk is in bovenstaand voorbeeld, is het in vele andere contexten veel minder duidelijk en worden er, vooral in de populaire literatuur, vaak causale beweringen gemaakt die niet (volledig) door de gegevens worden gestaafd. Volgend voorbeeld illustreert dit. Denk hierbij aan het voorbeeld van de associatie van groente consumptie en covid mortaliteit.
Een ecologische analyse is een statistische analyse waarbij men associaties bestudeert tussen samenvattingsmaten (zoals gemiddelden, incidenties, …) die reeds berekend werden voor groepen subjecten. Dit is het geval bij het covid voorbeeld uit de introductie waarbij men mortaliteit modellereert in functie van de gemiddelde dagelijkse groenteconsumptie per capita in verschillende landen. Wanneer men aldus een ecologische correlatie vaststelt voor groepen subjecten of individuen (in dit geval,landen), impliceert dat niet noodzakelijk dat deze correlatie ook voor de subjecten zelf opgaat. Volgend voorbeeld illustreert dit.

Voorbeeld 22: (Ecological fallacy)

Voor de 48 staten in de V.S. werden telkens 2 getallen berekend: het percentage van de mensen die in een ander land geboren zijn en het percentage geletterden. De correlatie ertussen bedraagt 0.53 (Robinson, 1950). Dit is een ecologische correlatie omdat de eenheid van de analyse de groep residenten uit een zelfde staat is, en niet de individuele residenten zelf. Deze ecologische correlatie suggereert dat mensen van vreemde afkomst doorgaans beter geschoold zijn (in Amerikaans Engels) dan de oorspronkelijke inwoners. Wanneer men echter de correlatie berekent op basis van de gegevens voor alle individuele residenten, bekomt men -0.11. De ecologische analyse is hier duidelijk misleidend: het teken van de correlatie is er positief omdat mensen van vreemde origine de neiging hebben om te gaan wonen in staten waar de oorspronkelijke bevolking relatief goed geschoold is.

Einde voorbeeld