In het oude China verzonden soldaten die langs de Chinese Muur gestationeerd waren rooksignalen van toren naar toren om de aantocht van vijandelijke troepen aan elkaar door te seinen. Op die manier konden boodschappen zich in een paar uur tijd verspreiden over een afstand van meer dan 750 kilometer.

De verdedigingslinie die door de Chinese Muur werd opgetrokken, vormde echter geen rechte lijn, maar een netwerk van aarden en stenen versterkingen die verschillende wachtposten met elkaar verbonden. Wachtposten die gebruikt werden om rooksignalen te verspreiden, waren doorgaans op een hoogte gebouwd om het waarnemen van de signalen zo optimaal mogelijk te laten verlopen.
Opgave
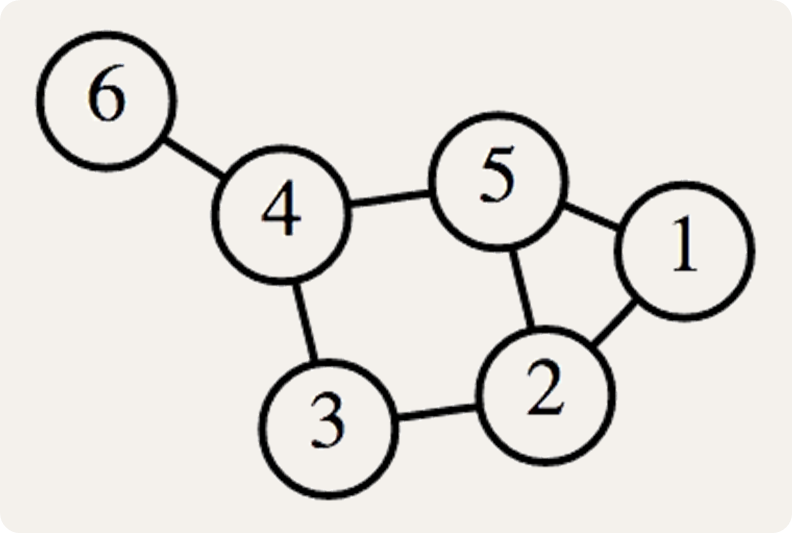
Hieronder hebben we een voorbeeld getekend van een netwerk van wachtposten langs de Chinese Muur waarop rooksignalen kunnen verzonden worden. De wachtposten worden voorgesteld door cirkels, en elke wachtpost wordt op een unieke manier gelabeld met een natuurlijk getal. Twee wachtposten worden door een lijn met elkaar verbonden als de rooksignalen die worden verzonden vanaf de ene wachtpost kunnen waargenomen worden op de andere wachtpost. Zo zie je dat in dit netwerk een rooksignaal dat wordt verzonden vanaf wachtpost 6 enkel kan waargenomen worden op wachtpost 4. Een rooksignaal dat wordt verzonden vanaf wachtpost 1 kan worden waargenomen op wachtposten 2 en 5. Van zodra door een wachtpost een rooksignaal wordt waargenomen, begint men vanaf die wachtpost ook rooksignalen te verzenden om zo de waarschuwing te verspreiden langs het volledige netwerk.
We stellen elke wachtpost voor door een uniek natuurlijk getal (int) dat gebruikt wordt om de wachtpost te identificeren.
Een netwerk van wachtposten wordt voorgesteld als een dictionary (dict) die elke wachtpost (int) in het netwerk afbeeldt op een verzameling (set) met alle naburige wachtposten (int) in het netwerk waarop zijn rooksignalen kunnen waargenomen worden. Daarbij is gegarandeerd dat alle wachtposten in het netwerk via naburige wachtposten met elkaar verbonden zijn. Het netwerk dat hierboven als voorbeeld gebruikt werd, wordt op deze manier beschreven door de volgende dictionary:
{1:{2, 5}, 2:{1, 5, 3}, 3:{2, 4}, 4:{3, 5, 6}, 5:{1, 2, 4}, 6:{4}}Gevraagd wordt:
-
Schrijf een functie waargenomen waaraan twee argumenten moeten doorgegeven worden: i) een verzameling (set) met alle wachtposten (int) in een netwerk waar een rooksignaal wordt opgelaten en ii) het netwerk van wachtposten (dict). De functie moet een verzameling (set) teruggeven met alle wachtposten (int) in het netwerk waarop rooksignalen worden waargenomen maar waar zelf geen rooksignaal wordt opgelaten.
-
Schrijf een functie verspreiding waaraan twee argumenten moeten doorgegeven worden: i) een wachtpost $$p$$ (int) en ii) het netwerk van wachtposten (dict). Op tijdstip nul wordt een rooksignaal verzonden vanaf wachtpost $$p$$ om een alarm te verspreiden. Na elke tijdsstap worden bijkomende rooksignalen verzonden vanaf alle wachtposten waarop een rooksignaal wordt waargenomen. De functie moet een natuurlijk getal (int) teruggeven dat aangeeft na hoeveel tijdsstappen het signaal verspreid werd over alle wachtposten in het netwerk.
Voorbeeld
>>> netwerk = {1:{2, 5}, 2:{1, 5, 3}, 3:{2, 4}, 4:{3, 5, 6}, 5:{1, 2, 4}, 6:{4}}
>>> waargenomen({1, 2}, netwerk)
{3, 5}
>>> waargenomen({3, 4}, netwerk)
{2, 5, 6}
>>> verspreiding(1, netwerk)
3
>>> verspreiding(4, netwerk)
2