Bijen maken honingraten van zeshoekige cellen die gemaakt zijn van bijenwas. De vorm van de cellen zorgt voor de meest efficiënte indeling van de raat, verhoogt de sterkte van de kam en vermindert de hoeveelheid was die nodig is om een robuuste structuur te produceren. Daardoor wordt de ruimte optimaal gebruikt om honing op te slaan en wordt energie bespaard bij de wasproductie, want de productie van één kilo was kost vier tot zes kilo honing.

In de natuur vinden we deze zeshoekige structuur ook terug in de vorm van grafiet, waarbij elk vel grafeen lijkt op kippengaas met sterke covalente koolstofbindingen. Er worden ook buisvormige grafeenplaten gesynthetiseerd die koolstofnanobuisjes genoemd worden. Ze hebben veel toepassingen vanwege hun hoge treksterkte en elektrische eigenschappen.

De schoonheid van de natuur wordt ondertussen ook binnenshuis nagebootst. Daar voegen mozaïekpatronen van zeszijdige tegels een uniek karakter en geometrische elegantie toe aan keukens, badkamers, woonkamers en slaapkamers. Deze veelzijdige tegels bieden een tijdloze afwerking en passen naadloos bij subtiele en gedurfde interieurs, waardoor ze een steeds populairdere keuze zijn voor wanden en vloeren in veel interieuromgevingen.

Opgave

Om patronen te beschrijven in roosters van zeshoekige cellen, hebben we een coördinatensysteem nodig dat de positie van elke cel op een unieke manier vastgelegt. We nemen een rooster waarin de zeshoeken met een punt naar boven liggen en gebruiken een axiaal coördinatensysteem. Daarin wordt de positie van elke cel aangeduid met een paar coördinaten $$(q, r)$$, waarbij $$q, r \in \mathbb{Z}$$.

Elke zeshoekige cel heeft zes buren die respectievelijk ten oosten (O), zuidoosten (ZO), zuidwesten (ZW), westen (W), noordwesten (NW) en noordoosten (NO) liggen. De richtingen waarin deze zes buren liggen, worden aangeduid door strings (str) met één of twee hoofdletters, zoals aangegeven in voorgaande oplijsting. Dit is het verband tussen de axiale coördinaten $$(q, r)$$ van een cel en de axiale coördinaten van zijn zes buren:

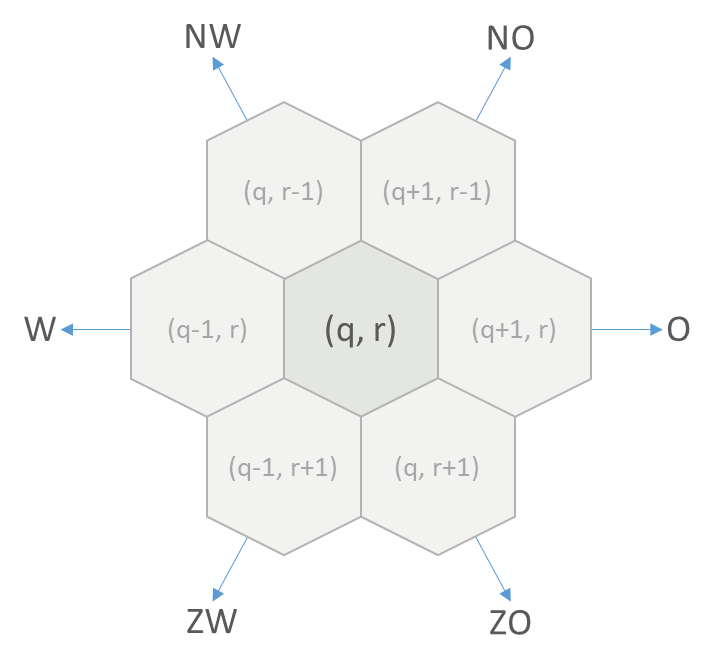
Als we in een rooster van zeshoekige cellen een referentiecel kiezen met axiale coördinaten $$(0, 0)$$, dan zijn dit de axiale coördinaten van de omliggende cellen:

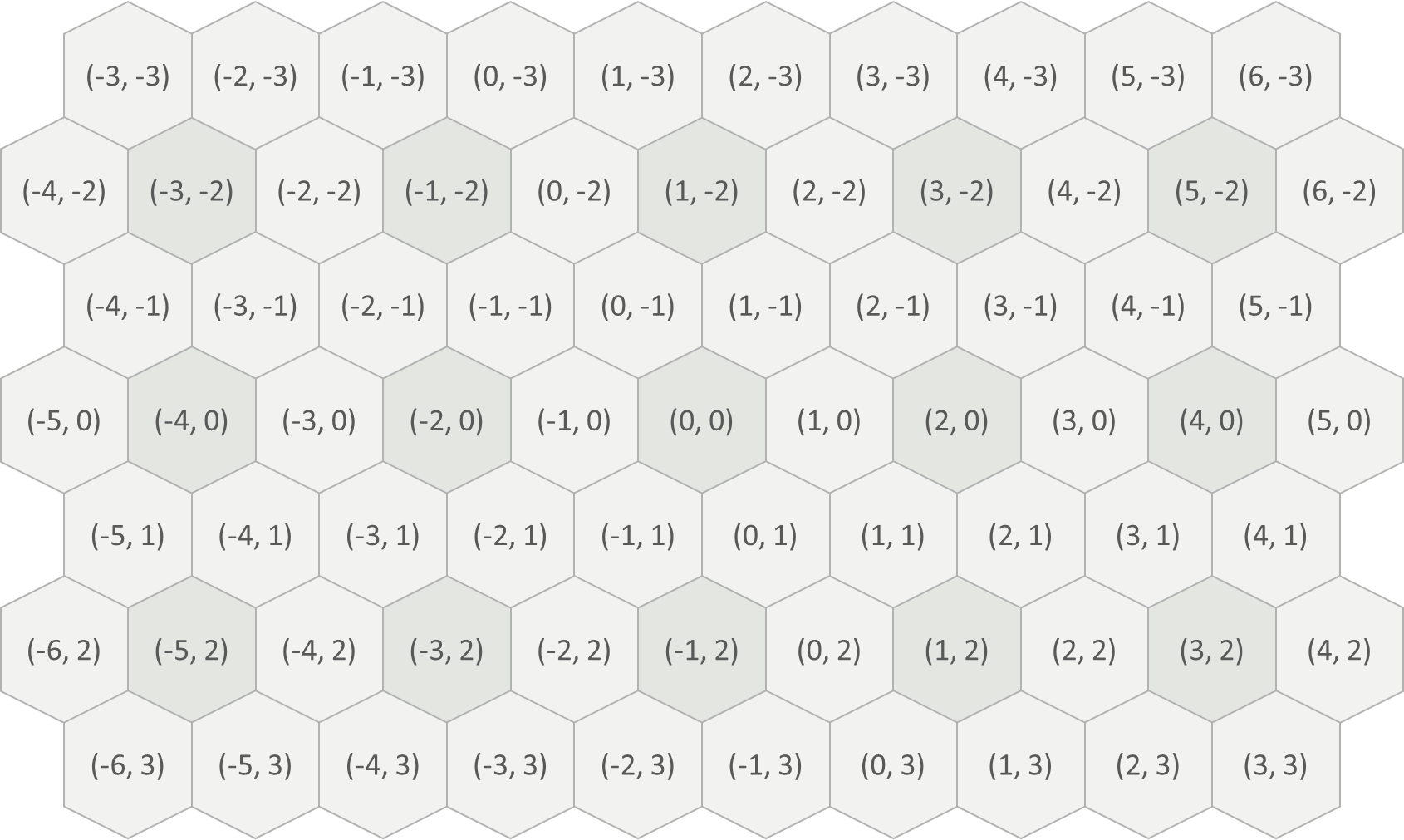
De afstand tussen een zeshoek $$z$$ met coordinaten $$(q, r)$$ en een zeshoek $$\bar{z}$$ met coördinaten $$(\bar{q}, \bar{r})$$ is gedefineerd als het minimaal aantal stappen naar naburige cellen dat je moet zetten om vanaf cel $$z$$ naar cel $$\bar{z}$$ te gaan. Deze afstand wordt berekend als \[ \frac{1}{2}(|q - \bar{q}| + |r - \bar{r}| + |q + r - \bar{q} - \bar{r}|) \] Hierbij staat $$|x|$$ voor de absolute waarde van $$x$$.

Definieer een klasse Zeshoek waarmee zeshoekige cellen (met puntige top) in een rooster met een axiaal coördinatensyteem kunnen voorgesteld worden. Bij het aanmaken van een zeshoek (Zeshoek) moeten de coördinaten $$q$$ (int) en $$r$$ (int) van de cel doorgegeven worden. Zeshoeken zijn onveranderlijk (immutable).

Als er een zeshoek $$z$$ (Zeshoek) wordt doorgegeven aan de ingebouwde functie str, dan moet die een beschrijving (str) van de positie van zeshoek $$z$$ teruggeven.

Als er een zeshoek $$z$$ (Zeshoek) wordt doorgegeven aan de ingebouwde functie repr, dan moet die een stringvoorstelling (str) teruggeven die leest als een Python expressie waarmee een nieuwe zeshoek (Zeshoek) aangemaakt wordt met dezelfde positie als zeshoek $$z$$.

Om zeshoeken (Zeshoek) aan verzamelingen (set) te kunnen toevoegen, moet de ingebouwde functie hash de hashwaarde van zeshoeken teruggeven en moet de operator == bepalen of twee zeshoeken gelijk zijn. Zorg ervoor dat een zeshoek (Zeshoek) met coördinaten $$(q, r)$$ dezelfde hashwaarde heeft als een tuple $$(q, r)$$. Zorg ervoor dat twee zeshoeken (Zeshoek) gelijk zijn als en slechts als ze zich op dezelfde positie in het rooster bevinden.

Voorts moet je op een zeshoek $$z$$ (Zeshoek) minstens de volgende methoden kunnen aanroepen:

• Een methode afstand waaraan een zeshoek $$\bar{z}$$ (Zeshoek) moet doorgegeven worden. De methode moet de afstand (int) tussen zeshoeken $$z$$ en $$\bar{z}$$ teruggeven.

• Een methode buur waaraan een richting $$r$$ (str) moet doorgegeven worden. De methode moet de buur (Zeshoek) van zeshoek $$z$$ in richting $$r$$ teruggeven.

• Een methode pad waaraan een beschrijving (str) moet doorgegeven worden van de richtingen van buurcellen die achtereenvolgens moeten bezocht worden vanaf zeshoek $$z$$. Deze richtingen worden aan elkaar geschreven zonder scheidingsteken. De methode moet de zeshoek (Zeshoek) teruggeven die bereikt wordt nadat het pad gevolgd werd vanaf zeshoek $$z$$.

• Een methode buren waaraan geen argumenten moeten doorgegeven worden. De methode moet een verzameling (set) teruggeven met de zes buren (Zeshoek) van zeshoek $$z$$.

Voorbeeld

>>> tegel = Zeshoek(0, 0)
>>> tegel
Zeshoek(0, 0)
>>> print(tegel)
(0, 0)
>>> tegel.afstand(Zeshoek(4, 3))
7

>>> tegel.buur('O').buur('ZO').buur('NO').buur('O')
Zeshoek(3, 0)
>>> tegel.buur('NW').buur('W').buur('ZW').buur('O').buur('O')
Zeshoek(0, 0)
>>> tegel.pad('OZONOO')
Zeshoek(3, 0)
>>> tegel.pad('NWWZWOO')
Zeshoek(0, 0)

>>> tegel.pad('OZONOO') == tegel
False
>>> tegel.pad('NWWZWOO') == tegel
True

>>> hash(tegel)
3713080549408328131

>>> tegel.buren()
{Zeshoek(0, 1), Zeshoek(-1, 1), Zeshoek(-1, 0), Zeshoek(0, -1), Zeshoek(1, 0), Zeshoek(1, -1)}