Opgave
In de Toer de Zwans krijgt een renner de vierkantjestrui als hij de meeste punten verzamelt op de bergtoppen. De regels zijn simpel: de eerste renner op een top krijgt 3 punten, de tweede 2, de derde 1 en de rest niks. De punten worden opgeteld en het totaal bepaalt de rangschikking in het bergklassement.Na de Toer doen ploegen een analyse van hun resultaten en hun tegenstanders. Daarbij komt heel wat hypothetisch gebazel kijken. Zo beweerde een renner wiens naam we om privacy redenen onherkenbaar met MRX1 aanduiden: als Van Impe niet had deelgenomen aan deze Toer, dan had ik het bergklassement gewonnen!
Dat zou kunnen: als Van Impe in de bergen wat punten pakte voor MRX, en Van Impe wordt uit alle uitslagen geschrapt, dan kan MRX inderdaad opschuiven in het bergklassement en misschien zelfs winnen.
Wat is nu de bedoeling van deze opgave? Zoek de renner die door zijn verwijdering uit alle uitslagen jou doet opschuiven naar de eerste plaats in de einduitslag in het bergklassement. Als er meer dan één zulke renner is, dan willen we elk van hun namen. Het is uiteraard ook mogelijk dat het elimineren van geen enkele concurrent helpt om je te laten winnen in het bergklassement: dat willen we dan ook weten.
Een voorbeeld met 5 cols; hier hebben de renners als naam een hoofdletter:
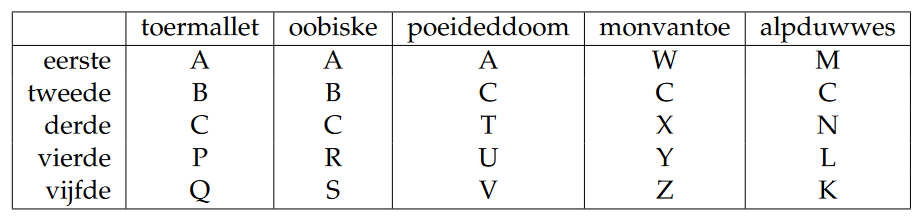
A was 3 keer eerste, heeft 9 punten. B was 2 keer tweede en heeft 4 punten.
C heeft 8 punten. De eindstand is (1) A (2) C (3) B.
Om A eerst te krijgen helpt niks, want A is al eerste. Dus is de uitvoer niks helpt.
Als jij renner B bent, dan verbetert het schrappen van A je uitslag: je hebt nu 6 punten, maar je eindigt op de tweede plaats na C vermits die er door het schrappen van A 11 heeft. Dus voor B niks helpt.
Als B wordt geschrapt, dan wint C (C heeft dan 10 punten). Maar ook door A te verwijderen wint C. En vergeet W en M niet ... C stijgt dus naar de eerste plaats door A, B, M of W te verwijderen: de uitvoer is A B M W.
Renner V kan niet verbeteren door een andere renner te verwijderen, dus schrijf je, voor V, uit niks helpt.
Voor alle andere renners ... niks helpt.
Zo zie je ook dat dezelfde uitslag voor verschillende renners een verschillende uitsluiting kan betekenen.
Voor de volledigheid: meer dan één renner kan het bergklassement winnen; dat gebeurt als alle winnaars evenveel punten hebben en niemand heeft er meer.
Invoer
Let op: in het voorbeeld werden de renners ge ̈ıdentificeerd door een letter.
Hier gebeurt dat met een nummer.
De eerste regel stelt het aantal testgevallen voor. Per testgeval volgt:
- een lijn met het aantal bergritten: minstens één
- een lijn met het aantal renners AR: renners zijn genummerd van 1 tot AR; AR is nooit groter dan 30
- dan voor elke bergrit een lijn met daarop de eerste 5 renners die over de top kwamen, in de volgorde van aankomst; niet elke renner komt in een top-5 voor natuurlijk
- dan volgt een lijn met het aantal renners AE > 0 van wie je moet nagaan of ze tot op de eerste positie kunnen komen door iemand anders te verwijderen
- dan volgt een lijn met de AE nummers van de bedoelde renners, telkens gescheiden door een blanco
Voorbeeldinvoer:
1
5
26
1 2 3 16 17
1 2 3 18 19
1 3 20 21 22
23 3 24 25 26
13 3 14 12 11
4
1 2 3 22
Uitvoer
Per testgeval moet je zoveel regels afdrukken als er renners zijn waarvoor de
uitslag verbeterd moet worden: elke regel begint met het nummer van het
testgeval, een blanco, het nummer van de renner voor wie een verbetering
gezocht werd, en nog een blanco. Dat gebeurt in de volgorde waarin die
renners gegeven waren op de laatste lijn van het testgeval.
Daarna volgt ofwel niks helpt ofwel een rij van (nummers van) renners
wiens uitsluiting zorgt dat de renner winnaar wordt in het eindklassement.
Meerdere renners worden afgedrukt gescheiden door een blanco, en in
alfabetische orde.
Voorbeelduitvoer:
1 1 niks helpt
1 2 niks helpt
1 3 1 2 13 23
1 22 niks helpt