Victoria amazonica is de grootste waterlelie ter wereld. Deze soort heeft een temperatuur van 27-30 °C nodig, wat zelfs in de tropen niet overal voorkomt. Ze komt van nature voor in stilstaand of langzaam stromend water in Brazilië, Colombia, Guyana en Peru. In België kan de plant bewonderd worden in de plantentuin van de Universiteit Gent (Gent) en de Nationale Plantentuin van België (Meise).
De bladeren van V. amazonica zijn kastanjebruin als ze het wateroppervlak bereiken, maar worden later groen. Jonge bladeren hebben korte, naar binnen omgekrulde randen. Oudere bladeren kunnen een diameter tot 3 meter bereiken. Ze hebben een 4–10 cm hoge rand en drijven aan 7 tot 8 meter lange stengels. De grootste bladeren hebben een draagvermogen van 40 kg. De bladeren zijn aan de onderkant bezet met stekels en opvallende ribben die een onregelmatig patroon van cellen vormen.

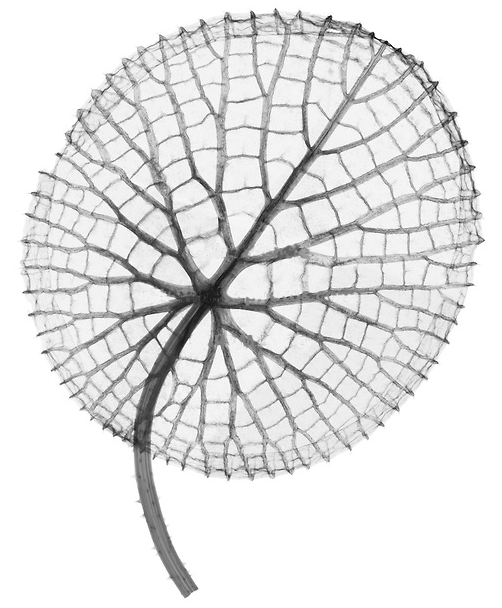
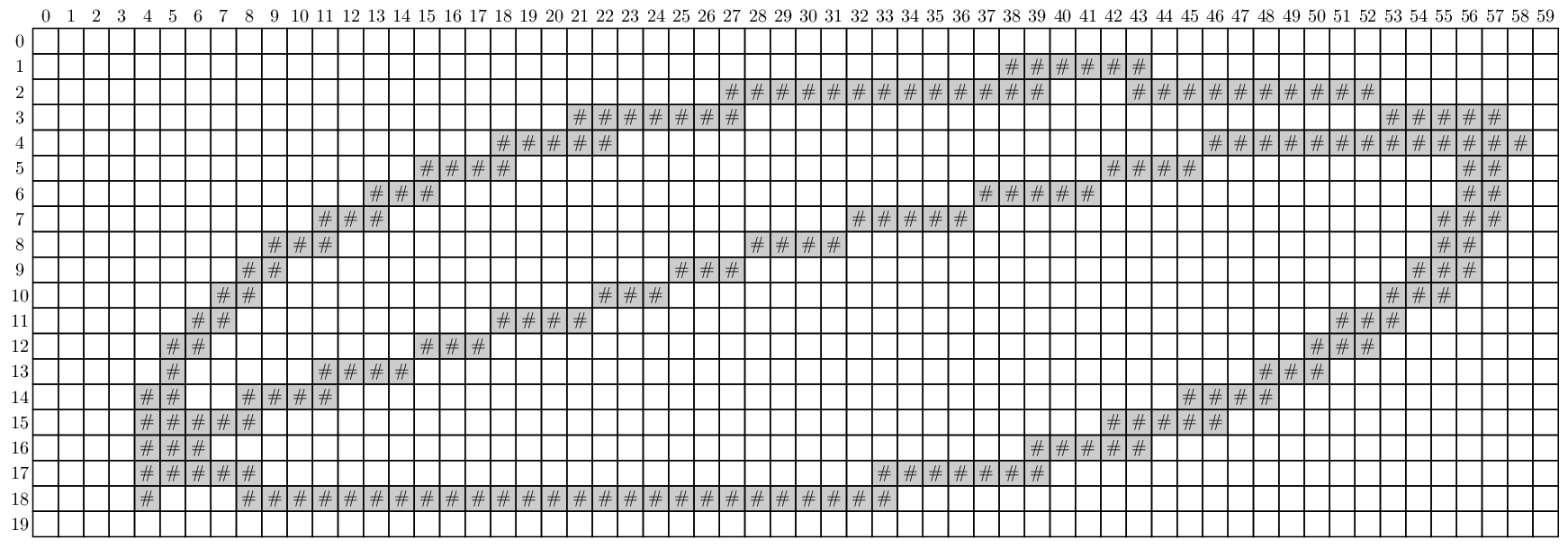
Om een plantensoort te onderzoeken willen we het aantal cellen aan de onderkant van zijn bladeren tellen en de gemiddelde grootte van een bladcel bepalen. Hiervoor zetten we telkens een afbeelding van een blad om in een bitmap waarin de bladcellen duidelijk afgelijnd zijn. Zo een bitmap is niets anders dan een rechthoekig rooster en de vakjes van dit rooster worden bits genoemd. Elke bit van het rooster is leeg (voorgesteld door een spatie) of wordt bedekt door een stuk rib van het blad (voorgesteld door een hekje: #). Als voorbeeld zie je hieronder een afbeelding van een eenvoudig blad met twee cellen (links) en de bitmap die we van deze afbeelding gemaakt hebben (rechts). In een bitmap wordt een bladcel gevormd door een gebied van aangrenzende lege bits. Bits worden hierbij aangrenzend genoemd als ze een gemeenschappelijke zijde hebben. Een gebied van aangrenzende lege bits wordt nooit als een bladcel beschouwt als het bits op de buitenste rand van de bitmap bevat.

Opgave
Definieer een klasse Blad waarmee bladeren van planten kunnen geanalyseerd worden. De objecten van deze klasse moeten minstens de volgende methoden hebben:
Een initialisatiemethode __init__ waaraan de locatie van een tekstbestand moet doorgegeven worden. Dit tekstbestand bevat een bitmap van het blad dat moet geanalyseerd worden.
Een methode __str__ die een stringvoorstelling van het blad teruggeeft. Deze stringvoorstelling geeft het rechthoekig rooster weer zoals het uit het opgegeven bitmapbestand werd gelezen. Naast lege bits (voorgesteld door spaties) en bits die samenvallen met ribben van het blad (voorgesteld door hekjes: #), kunnen bits daarnaast ook opgevuld zijn (voorgesteld door punten). Dit opvullen gebeurt door het aanroepen van de methode opvullen (zie verder).
Een methode opvullen waaraan het rij- en kolomnummer van een lege bit in de bitmap moet doorgegeven worden. De rijen van een bitmap worden genummerd van boven naar onder, de kolommen van links naar rechts, en de nummering start telkens vanaf nul. Indien de bit op de opgegeven positie niet leeg is, moet de methode een AssertionError opwerpen met de tekst bit moet leeg zijn. Anders moeten alle bits van het gebied van aangrenzend lege bits waartoe de opgegeven bit behoort als opgevuld gemarkeerd worden (ze worden dus niet langer als leeg beschouwd nadat de methode werd aangeroepen) en moet de methode teruggeven uit hoeveel bits dit gebied bestaat.
Een methode wissen die alle opgevulde bits van de bitmap terug als leeg markeert. Merk op dat de opgevulde bits in de bitmap mogelijks tot meerdere cellen kunnen behoren, bijvoorbeeld als de methode opvullen verschillende keren werd aangeroepen voordat de methode wissen wordt aangeroepen.
Gebruik de methoden opvullen en wissen om een methode cellen te schrijven die het aantal bladcellen teruggeeft die niet kleiner zijn dan de opgegeven minimale celgrootte. De minimale celgrootte kan doorgegeven worden aan de optionele parameter minimum (standaardwaarde: 1). De grootte van een bladcel wordt uitgedrukt als het aantal bits in het overeenkomstige gebied van aaneengesloten lege bits in de bitmap. Het gebruik van een minimale celgrootte is belangrijk om kleine artefacten uit te sluiten die kunnen ontstaan bij het omzetten van de afbeelding van het blad naar de overeenkomstige bitmap. We merken hier opnieuw op dat gebieden van aaneengesloten lege bits die bits op de buitenste rand van de bitmap bevatten niet als bladcel mogen beschouwd worden. Deze gebieden moeten dus genegeerd worden als de methode de bladcellen telt. Zorg ervoor dat de bitmap geen opgevulde bits heeft nadat de methode werd aangeroepen.
Gebruik de methoden opvullen en wissen om een methode celgrootte te schrijven die de gemiddelde celgrootte teruggeeft van alle bladcellen die niet kleiner zijn dan de opgegeven minimale celgrootte. De minimale celgrootte kan doorgegeven worden aan de optionele parameter minimum (standaardwaarde: 1). Net zoals de vorige methode mag ook deze methode de gebieden van aaneengesloten lege bits die bits op de buitenste rand van de bitmap bevatten niet als bladcellen beschouwen, en mag de bitmap ook geen opgevulde bits vertonen na het aanroepen van de methode. De methode moet de waarde None teruggeven indien er geen bladcellen zijn die groter of gelijk zijn dan de opgegeven minimale celgrootte.
Voorbeeld
Bij onderstaande voorbeeldsessie gaan we ervan uit dat de tekstbestanden blad.txt en victoria.txt zich in de huidige directory bevinden. Het eerste bestand bevat de bitmap die gemaakt werd van de afbeelding van het eenvoudige blad dat hierboven als voorbeeld gebruikt werd. Het tweede bestand bevat een bitmap die gemaakt werd op basis van de afbeelding met de onderkant van een blad van de V. amazonica die we in de inleiding van deze opgave gebruikt hebben.
>>> blad = Blad('blad.txt')
>>> print(blad)
<BLANKLINE>
######
############# ##########
####### #####
##### #############
#### #### ##
### ##### ##
### ##### ###
### #### ##
## ### ###
## ### ###
## #### ###
## ### ###
# #### ###
## #### ####
##### #####
### #####
##### #######
# ##########################
<BLANKLINE>
>>> blad.opvullen(5, 30)
182
>>> print(blad)
<BLANKLINE>
######
#############...##########
#######.........................#####
#####.......................#############
####.......................#### ##
###.....................##### ##
###..................##### ###
###................#### ##
##...............### ###
##.............### ###
##..........#### ###
##........### ###
#.....#### ###
##..#### ####
##### #####
### #####
##### #######
# ##########################
<BLANKLINE>
>>> blad.opvullen(8, 30)
Traceback (most recent call last):
AssertionError: bit moet leeg zijn
>>> blad.opvullen(15, 30)
335
>>> print(blad)
<BLANKLINE>
######
#############...##########
#######.........................#####
#####.......................#############
####.......................####..........##
###.....................#####..............##
###..................#####..................###
###................####.......................##
##...............###..........................###
##.............###............................###
##..........####.............................###
##........###................................###
#.....####.................................###
##..####.................................####
#####.................................#####
###................................#####
#####........................#######
# ##########################
<BLANKLINE>
>>> blad.wissen()
>>> print(blad)
<BLANKLINE>
######
############# ##########
####### #####
##### #############
#### #### ##
### ##### ##
### ##### ###
### #### ##
## ### ###
## ### ###
## #### ###
## ### ###
# #### ###
## #### ####
##### #####
### #####
##### #######
# ##########################
<BLANKLINE>
>>> blad.cellen()
2
>>> blad.celgrootte()
258.5
>>> victoria = Blad('victoria.txt')
>>> victoria.cellen()
242
>>> victoria.cellen(minimum=10)
219
>>> victoria.cellen(minimum=20)
213
>>> victoria.celgrootte()
107.86363636363636
>>> victoria.celgrootte(minimum=10)
118.74885844748859
>>> victoria.celgrootte(minimum=20)
121.64319248826291