De tweeling Hans en Grietje woont samen met vader en stiefmoeder temidden van een uitgestrekt bos. Om te voorkomen dat zijn kinderen tijdens hun spel zouden verdwalen, heeft vader op een kaart van het bos een rechthoekig rooster getekend waarbij opeenvolgende roosterlijnen telkens op 50 meter afstand van elkaar liggen. Hun huis is op die kaart gelegen op het punt met coördinaat $$(0, 0)$$. Aan de bomen in het bos die op de kruising van twee roosterlijnen liggen, heeft vader een geel lintje bevestigd met daarop de $$(x, y)$$ coördinaten van de boom, waarbij de $$x$$-coördinaat aangeeft op hoeveel verticale roosterlijnen rechts van het huis de boom staat en de $$y$$-coördinaat aangeeft horizontale roosterlijnen boven het huis de boom staat.

Als de kinderen hun huis verlaten om het bos in te trekken, dan mogen ze van vader telkens naar een volgende boom met een geel lintje gaan die zich op 50 meter boven, onder, links of rechts van hun huidige positie bevindt als de som van de cijfers van de $$x$$-coördinaat en de $$y$$-coördinaat op het lintje aan die boom niet groter is dan hun leeftijd (uitgedrukt in jaren). De boom op positie $$(12, 24)$$ kunnen ze dus enkel bereiken als ze ten minste $$1 + 2 + 2 + 4 = 9$$ jaar oud zijn. Bij elke boom die ze bezoeken moeten ze ook een broodkruimel achterlaten om hun weg niet te verliezen. Hans en Grietje maken er bij elke verjaardag dan ook een spelletje van om te berekenen hoeveel punten in het bos (hun huis en de bomen waaraan een geel lintje hangt) ze dat jaar zullen kunnen bereiken. Op onderstaande kaart hebben ze de 41 punten aangeduid die ze vanaf hun vierde verjaardag kunnen bereiken.

Kaart met de 41 punten die Hans en Grietje vanaf hun vierde verjaardag kunnen bereiken.

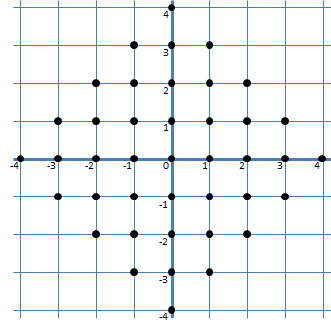
Merk op dat als Hans en Grietje tien jaar of ouder zijn, het niet langer zo is dat alle punten binnen een vierkant (45 graden geroteerd) rondom hun huis bereikbaar zijn. Hieronder tonen we nog een aantal figuren waarop de bereikbare punten in het wit staan aangegeven als Hans en Grietje $$n$$ jaar oud zijn.

Kaarten waarop de punten in het wit zijn aangeduid die Hans en Grietje kunnen bereiken als ze $$n$$ jaar oud zijn.

Opgave

De coördinaat van een punt in het bos wordt voorgesteld door een tuple $$(x, y)$$, waarbij $$x, y \in \mathbb{Z}$$ (int). Gevraagd wordt:

Schrijf een functie bereikbaar waaraan twee argumenten moeten doorgegeven worden: i) de coördinaat $$(x, y)$$ van een punt in het bos en ii) een getal $$n \in \mathbb{N}$$ (int). De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of de som van de cijfers van $$x$$ en $$y$$ kleiner of gelijk is aan $$n$$.
Schrijf een functie buren waaraan de coördinaat $$(x, y)$$ van een punt in het bos moet doorgegeven worden. De functie moet een verzameling (set) teruggeven met de coördinaten van de vier punten in het bos die op 50 meter afstand van het gegeven punt liggen.
Schrijf een functie broodkruimels waaraan een getal $$n \in \mathbb{N}$$ (int) moet doorgegeven worden die de leeftijd (in jaren) van Hans en Grietje voorstelt. De functie moet een verzameling (set) teruggeven met de coördinaten van alle punten in het bos die Hans en Grietje dat jaar kunnen bereiken.

Algoritme

Om de coördinaten te bepalen van alle punten die Hans en Grietje kunnen bereiken als ze $$n$$ jaar oud zijn, kan je het volgende algoritme toepassen dat gebruikmaakt van twee verzamelingen: een verzameling $$\mathcal{B}$$ van de bereikbare punten en een verzameling $$\mathcal{R}$$ van punten waarvan de buren nog moeten onderzocht worden:

initialisatie: $$\mathcal{B} = \emptyset,\mathcal{R} = \{(0, 0)\}$$
haal een willekeurig punt $$p$$ uit $$\mathcal{R}$$
voeg $$p$$ toe aan $$\mathcal{B}$$
voeg de buren van $$p$$ toe aan $$\mathcal{R}$$ als die buren bereikbaar zijn en nog niet in $$\mathcal{B}$$ zitten
herhaal vanaf stap 2 totdat $$\mathcal{R} = \emptyset$$

Hierbij stelt $$\emptyset$$ de lege verzameling voor.

Voorbeeld

>>> bereikbaar((0, 0), 0)
True
>>> bereikbaar((10, 20), 3)
True
>>> bereikbaar((2, 3), 4)
False

>>> buren((0, 0))
{(0, 1), (0, -1), (1, 0), (-1, 0)}
>>> buren((4, 3))
{(4, 2), (4, 4), (3, 3), (5, 3)}

>>> broodkruimels(0)
{(0, 0)}
>>> broodkruimels(2)
{(0, 1), (-1, 1), (0, 0), (-1, 0), (0, -2), (0, 2), (2, 0), (-1, -1), (0, -1), (1, 0), (1, -1), (1, 1), (-2, 0)}
>>> len(broodkruimels(10))
1121
>>> len(broodkruimels(19))
102485