We previously described how boxplots show outliers, but we did not provide a precise definition. Here we discuss outliers, approaches that can help detect them, and summaries that take into account their presence.
Outliers are very common in data science. Data recording can be complex and it is common to observe data points generated in error. For example, an old monitoring device may read out nonsensical measurements before completely failing. Human error is also a source of outliers, in particular when data entry is done manually. An individual, for instance, may mistakenly enter their height in centimeters instead of inches or put the decimal in the wrong place.
How do we distinguish an outlier from measurements that were too big or too small simply due to expected variability? This is not always an easy question to answer, but we try to provide some guidance. Let’s begin with a simple case.
Suppose a colleague is charged with collecting demography data for a group of males. The data report height in feet and are stored in the object:
library(tidyverse)
library(dslabs)
data(outlier_example)
str(outlier_example)
#> num [1:500] 5.59 5.8 5.54 6.15 5.83 5.54 5.87 5.93 5.89 5.67 ...
Our colleague uses the fact that heights are usually well approximated by a normal distribution and summarizes the data with average and standard deviation:
mean(outlier_example)
#> [1] 6.1
sd(outlier_example)
#> [1] 7.8
and writes a report on the interesting fact that this group of males is much taller than usual. The average height is over six feet tall! Using your data science skills, however, you notice something else that is unexpected: the standard deviation is over 7 feet. Adding and subtracting two standard deviations, you note that 95% of this population will have heights between -9.489, 21.697 feet, which does not make sense. A quick plot reveals the problem:
boxplot(outlier_example)
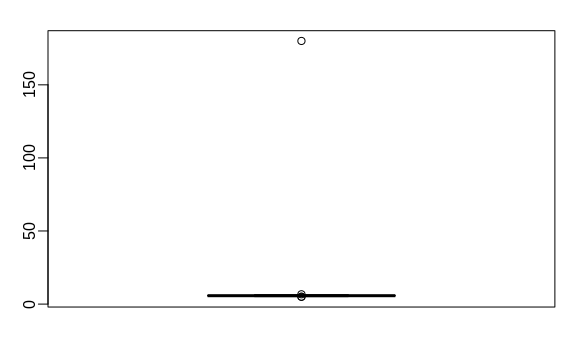
There appears to be at least one value that is nonsensical, since we know that a height of 180 feet is impossible. The boxplot detects this point as an outlier.