Het enige uurwerk dat Andrea in huis heeft, is een grote staande klok. Op een dag is ze vergeten om de klok op te winden, waardoor de klok gestopt is met tikken. Enkele dagen later reist ze naar de stad om er te gaan lunchen bij een vriendin wiens klok altijd de correcte tijd aangeeft. Onmiddellijk nadat ze thuiskomt, maakt ze een eenvoudige berekening waarmee ze haar klok terug juist kan zetten.
Hoe is ze daarin geslaagd zonder de exacte reistijd te kennen tussen haar huis en dat van haar vriendin?
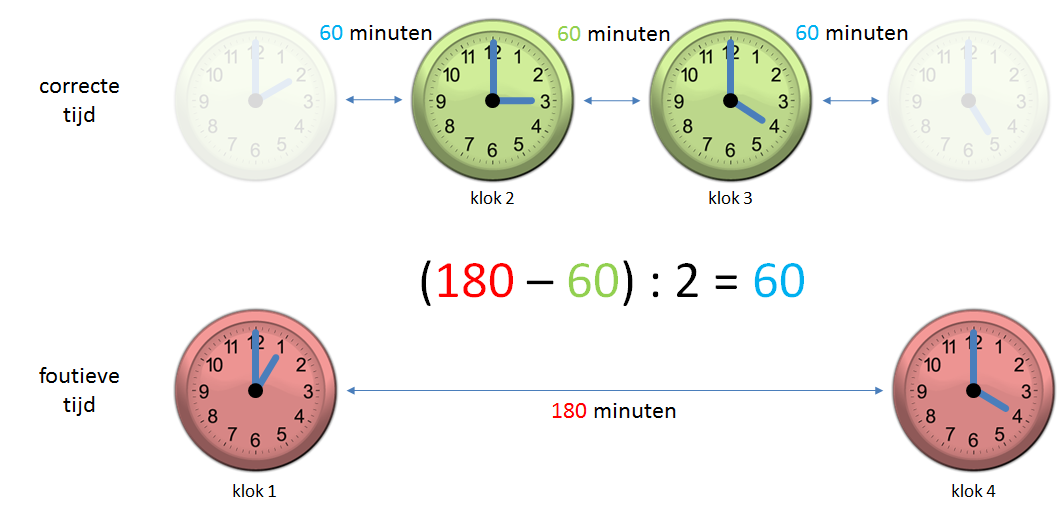
Na eventjes zoeken zou men de volgende strategie kunnen vinden. Vooraleer haar huis te verlaten, windt Andrea haar staande klok terug op en onthoudt ze de tijd die de klok bij vertrek aangeeft. Daarna onthoudt ze ook de correcte tijd die de klok in het huis van haar vriendin aangeeft, zowel bij aankomst als bij vertrek. Als ze terug thuiskomt, kan ze op basis van de tijd die haar klok aangeeft, bepalen hoeveel tijd de volledige trip geduurd heeft. Daar trekt ze de tijd van af die ze in het huis van haar vriendin heeft doorgebracht, en deelt het resultaat door twee om de reistijd tussen haar huis en dat van haar vriendin te weten te komen. Als ze deze tijdsduur optelt bij de tijd die de klok aangaf als ze bij het huis van haar vriendin vertrok, dan bekomt ze de huidige tijd waarmee ze haar eigen klok kan instellen.
Invoer
Acht natuurlijke getallen die elk op een afzonderlijke regel staan. Elk paar opeenvolgende getallen $$h$$ ($$0 \leq h < 24$$) en $$m$$ ($$0 \leq m < 60$$) correspondeert met de tijdsaanduiding $$h\text{:}m$$ op een 24-uursklok. De vier tijdsaanduidingen geven achtereenvolgens de tijd aan op het ogenblik dat Andrea
-
vertrekt vanaf haar eigen huis
-
aankomt bij het huis van haar vriendin
-
terug vertrekt vanaf het huis van haar vriendin
-
terug aankomt bij haar eigen huis
Uitvoer
Twee regels met de natuurlijke getallen $$h$$ ($$0 \leq h < 24$$) en $$m$$ ($$0 \leq m < 60$$) die corresponderen met de correcte tijd $$h\text{:}m$$ op een 24-uursklok wanneer Andrea terug aankomt bij haar eigen huis. Je mag ervan uitgaan dat Andrea niet langer dan 24 uur van huis is weggeweest.
Voorbeeld
Invoer:
13
0
15
0
16
0
16
0Uitvoer:
17
0