Blinkenlights is een neologisme uit de hackercultuur die van oorsprong refereert aan de diagnostische lampjes op mainframe¹-computers uit de jaren 60 en 70. Volgens de Jargon file² dateert de term al uit de jaren 50 en werd hij in de jaren 60 wereldwijd waargenomen. Vandaag wordt de term nog gebruikt voor de statuslampjes van moderne netwerkhardware (modems, netwerkhubs, etc.). Computer hebben nu om tal van redenen geen blinkenlights meer, maar de belangrijkste is dat mensen computers niet langer kunnen volgen door de snelheid waarmee moderne CPU's rekenen. Hoewel er sindsdien meer geavanceerde UI³-mechanismen zijn ontwikkeld, kunnen blinkenlights nog steeds aanwezig zijn als aanvullende statusindicatoren en vertrouwde skeuomorfismen⁴.

Hackers⁶ hebben de term ontleend aan een beroemd nep-waarschuwingsbord met tekst (vaak in Gotisch lettertype⁷) geschreven in steenkolenduits dat bijna homoniem is met Engelse termen. Er is zelfs een Duitse versie die de parodie parodieert.

Opgave

Klare tekst en cijfertekst zijn twee begrippen uit de cryptografie — Oudgrieks: κρυπτός (kryptós, "verborgen, geheim") en γράφειν (gráphein, "schrijven") — de toepassing en de studie van technieken waarmee een klare (leesbare) tekst kan versleuteld worden naar een onleesbare cijfertekst, die op zijn beurt terug kan ontsleuteld worden tot de oorspronkelijke klare tekst. De klare tekst is de oorspronkelijke (leesbare) tekst. De versleutelde (onleesbare) tekst heet de cijfertekst. De woorden versleutelen (klare tekst omzetten naar cijfertekst) en ontsleutelen (cijfertekst omzetten naar klare tekst) verwijzen naar het feit dat er bij het versleutelen en ontsleutelen vaak een sleutel moet gebruikt worden: een extra stuk (geheime) informatie dat je nodig hebt om die acties te kunnen uitvoeren.

We hebben berichten versleuteld met een cryptografische techniek waarbij de sleutel en de cijfertekst even lang zijn (uit evenveel karakters bestaan). De cijfertekst kan je ontsleutelen door de sleutel boven de cijfertekst te zetten. Als voorbeeld gebruiken we deze sleutel en cijfertekst:

    sleutel: e = 2.718281828459045235360287471352662497757247093699959574966967627724076
cijfertekst: 28 ZsTpaumnrhsrkotDscf nameggi cit rhi reenfeie  tüd enomntpeikadrtnenbu !g

Eerst lezen we de sleutel van links naar rechts, op zoek naar de positie waar het cijfer 0 de eerste keer voorkomt. Op die positie in de cijfertekst staat het eerste karakter van de klare tekst: in het voorbeeld is dat de hoofdletter D op positie 18 (als we de karakters van links naar rechts nummeren vanaf nul). Dan lezen we opnieuw de sleutel vanaf het begin, op zoek naar de positie waar het cijfer 1 de eerste keer voorkomt. Op die positie in de cijfertekst staat het tweede karakter van de klare tekst: in het voorbeeld is dat de letter a op positie 7. We herhalen dit om te zoeken waar de cijfers 2–9 voor het eerst voorkomen in de sleutel: we vinden achtereenvolgens de letter s (onder de eerste 2 op positie 4), een spatie (onder de eerste 3 op positie 22), de letter k (onder de eerste 4 op positie 15), de letter o (onder de eerste 5 op positie 16), de letter m (onder de eerste 6 op positie 25), de letter p (onder de eerste 7 op positie 6), de letter u (onder de eerste 8 op positie 8) en de letter t (onder de eerste 9 op positie 17).

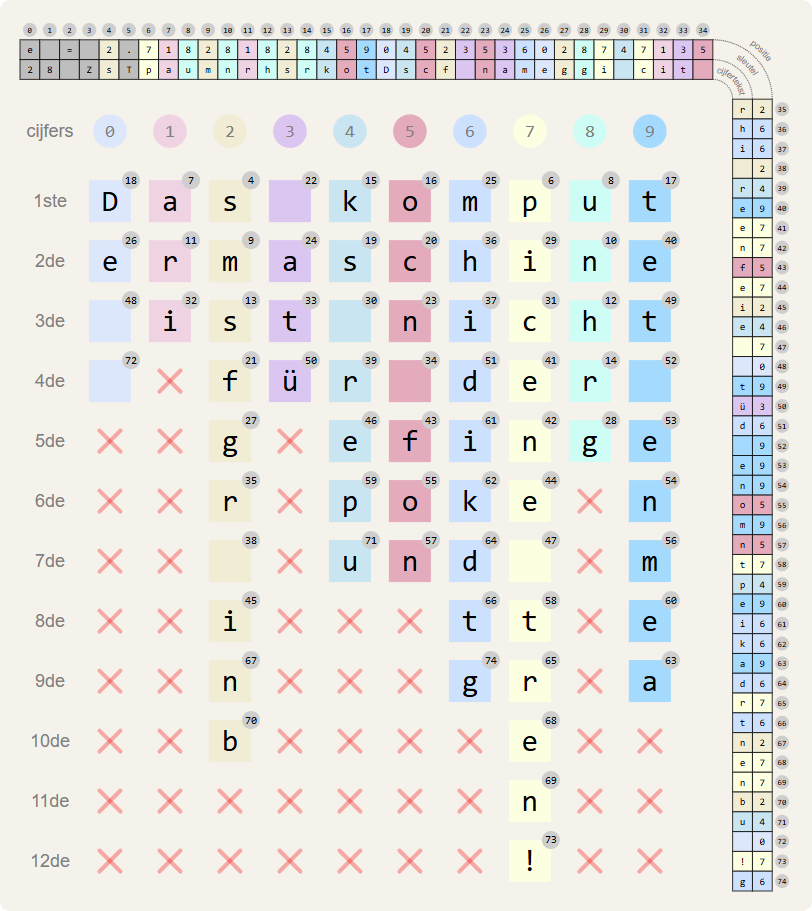
Als we daarmee klaar zijn, herhalen we de procedure terug van voor af aan, maar nu zoeken we telkens naar de tweede keer dat de cijfers 0–9 in de sleutel voorkomen. Op diezelfde posities vinden we in de cijfertekst de volgende karakters van de klare tekst. Ook dit blijven we herhalen om achtereenvolgens te zoeken waar de cijfers 0–9 de derde keer, de vierde keer, … in de sleutel voorkomen. Als een cijfer $$c$$ minder dan $$i$$ keer voorkomt in de sleutel, dan voegen we geen nieuw karakter toe aan de klare tekst als we zoeken waar het cijfer $$c$$ voor de $$i$$-de keer voorkomt in de sleutel. De procedure stopt zodra we voor alle cijfers uit de sleutel het overeenkomstige karakter uit de cijfertekst hebben toegevoegd aan de klare tekst.

De klare tekst is dus even lang (bevat evenveel karakters) als het aantal cijfers in de sleutel. De karakters in de cijfertekst die niet onder een cijfer van de sleutel staan, maken geen deel uit van de klare tekst. Daardoor kan de klare tekst korter zijn dan de cijfertekst en de sleutel. Voor de cijfertekst en de sleutel uit het voorbeeld krijgen we deze klare tekst:

klare tekst: Das komputermaschine ist nicht für der gefingerpoken und mittengraben!

Gevraagd wordt:

• Schrijf een functie aantal_cijfers waaraan een string $$s$$ (str) moet doorgegeven worden. De functie moet het aantal cijfers (int) in string $$s$$ teruggeven.

• Schrijf een functie positie_cijfer waaraan drie argumenten moeten doorgegeven worden: i) een cijfer $$c$$ (int; $$0 \leq c \leq 9$$), ii) een getal $$i$$ (int; $$i \in \mathbb{N}_0$$) en iii) een string $$s$$ (str). Als het cijfer $$c$$ minder dan $$i$$ keer voorkomt in string $$s$$, dan moet de waarde -1 (int) teruggegeven worden. Anders moet de positie (int) teruggegeven worden waar het cijfer $$c$$ voor de $$i$$-de keer voorkomt in string $$s$$. Posities van de karakters in string $$s$$ worden van links naar rechts genummerd vanaf nul. Het aantal voorkomens tellen we ook van links naar rechts.

• Schrijf een functie ontsleutel waaraan twee argumenten moeten doorgegeven worden: i) een cijfertekst $$t$$ (str) en ii) de sleutel $$s$$ (str) waarmee die kan ontsleuteld worden. De functie moet de klare tekst (str) teruggeven die bekomen wordt door bovenstaande ontsleutelingsprocedure toe te passen op cijfertekst $$t$$ met sleutel $$s$$.

Voorbeeld

>>> cijfertekst = '28 ZsTpaumnrhsrkotDscf nameggi cit rhi reenfeie  tüd enomntpeikadrtnenbu !g'
>>> sleutel = 'e = 2.718281828459045235360287471352662497757247093699959574966967627724076'

>>> aantal_cijfers(sleutel)
70

>>> positie_cijfer(3, 2, sleutel)
24
>>> positie_cijfer(6, 3, sleutel)
37
>>> positie_cijfer(9, 42, sleutel)
-1

>>> ontsleutel(cijfertekst, sleutel)
'Das komputermaschine ist nicht für der gefingerpoken und mittengraben!'

>>> cijfertekst = ' ftLsrnUisyTelvWya les   Kahen  Eu9ocr RRll 5ochyV.!s ynle5ITiRta'
>>> sleutel = '6630295(160n897o0338533q1=884868J7Z624$fJ035W3375E13016898B4X9.74'
>>> ontsleutel(cijfertekst, sleutel)
'Listen very carefully. I shall say this only once!'

Epiloog

Net zoals de "Listen very carefully. I shall say this only once!" uit het voorbeeld, hebben we ons voor het testen van ingediende oplossingen geïnspireerd op uitspraken uit 'Allo 'Allo!⁸. De BBC zond tussen 1982 en 1992 in totaal 85 aflevering uit van deze Britse komediereeks. Ze is deels als parodie op Secret Army⁹ bedacht en ontwikkeld door Jeremy Lloyd¹⁰ en David Croft¹¹, die ook de meeste afleveringen geschreven hebben. De hoofdrollen werden vertolkt door Gorden Kaye¹², Carmen Silvera¹³, Vicki Michelle¹⁴ en Sue Hodge¹⁵. De reeks staat bekend als een van de succesvolste Britse komedies aller tijden.

In de reeks worden zogezegd de volgende talen gesproken: Frans, Duits, Italiaans, Spaans, Zweeds (in seizoen 6) en Engels. In werkelijkheid spreken alle acteurs Engels, maar met verschillende accenten om de verschillende talen te benadrukken. De Britten in de reeks spreken met een opvallend deftig accent, en gebruiken typisch Britse woorden en uitdrukkingen, zoals chinwag (babbeltje), chaps (kerels) en peckish (hongerig). Fransen noemen zij Frogs en Duitsers Jerries. Bijna alle personages kunnen elkaar verstaan, maar er is een taalbarrière tussen de Fransen en de Britse piloten, net als tussen de Britten en de Duitsers.

Door deze taalbarrière kon er een gimmick ingebouwd worden rondom het personage van officer Crabtree. Crabtree is een Brit die maar "zeer matig" Frans spreekt. Om dit effect te benadrukken, zegt hij vaak woorden verkeerd, zoals Good moaning¹⁶, een running gag in de reeks. Soms ontstaan zo schuttingwoorden. Voorbeelden zijn: The bummers pissed over on a dick night in plaats van The bombers passed over on a dark night, I was pissing your coffee when I thought I'd drip in for a drunk in plaats van I was passing your cafe when I thought I'd drop in for a drink en Long distance dick in plaats van duck. Dit gebeurt echter alleen maar als hij met een "Frans accent" spreekt. Als hij in gesprek is met andere Britten, is zijn rare uitspraak ineens verdwenen, omdat hij dan "Engels" spreekt.

Later wordt er ook een andere grap opgevoerd met kapitein Hans Geering in Londen; oorspronkelijk sprak hij met een Duits accent en een nogal schuchtere, hoge stem. Wanneer hij echter in Londen met Britten praat, spreekt hij met een diepe stem op vrij deftige toon.