We beschouwen voor deze oefening een reeks van getallen $$n_0$$, $$n_1$$, $$n_2$$ ... die als volgt opgebouwd wordt:

1. Vertrek van een willekeurig geheel getal $$n_0 > 1$$
2. Het volgende getal wordt telkens als volgt bepaald:
   • Als het getal $$n_i$$ even is, dan wordt het gedeeld door 2, $$n_{i+1}$$ = $$n_i$$ / 2
   • Als het getal $$n_i$$ oneven is, dan is $$n_{i+1}$$ = $$n_i$$ * 3 +1

Op deze manier krijgen we steeds nieuwe getallen die ofwel groter zijn, ofwel kleiner zijn. Dit gaat zo verder tot we uiteindelijk bij het getal 1 uitkomen, dan stopt de reeks.

Afhankelijk van het getal waarmee we starten, kan het het getal 1 snel bereikt worden, of kunnen heel wat stappen nodig zijn, waarbij soms eerst heel grote getallen bekomen worden alvorens ze weer kleiner worden. Hoewel dit niet wiskundig is aangetoond, komen we steeds uit bij het getal 1. Het grootste getal dat onderweg bereikt wordt, noemen we de piek van de reeks.

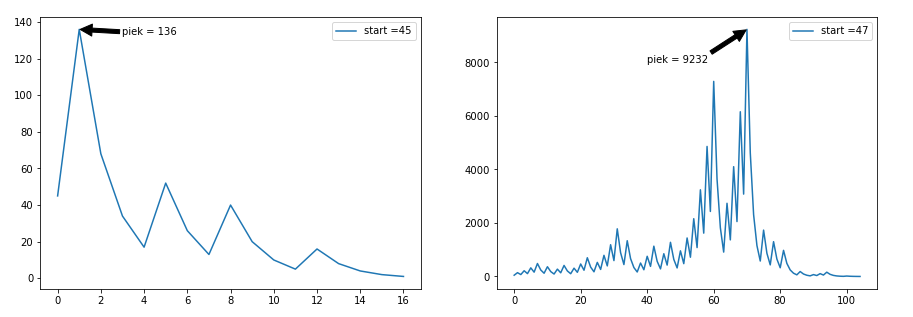
Als we twee startgetallen nemen die zeer dicht bij elkaar liggen, kan de reeks er toch helemaal anders uitzien:

• voor het startgetal $$n_0$$ = 45, krijgen we volgende reeks met 16 iteraties: 45, 136, 68, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
• voor het startgetal $$n_0$$ = 47, krijgen we daarentegen een reeks met 104 iteraties: 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1

Opgave

Schrijf een functie hoogste_piek die als argumenten twee gehele getallen $$m$$ en $$n$$ aanneemt ($$m < n$$).

De functie gaat voor elk startgetal tussen $$m$$ en $$n$$ (inclusief grenzen) na wat de piek is van de reeks zoals hierboven beschreven.

De functie retourneert één geheel getal, namelijk het startgetal waarvoor deze piek het hoogste is.

Voorbeeld

>>> hoogste_piek(45, 100)
47

>>> hoogste_piek(3876, 4339)
4255